Category Aircraft Flight

The idea of using a gas turbine to produce jet propulsion was developed quite independently by Whittle in England and von Ohain and others in Germany in the 1930s. Neither Whittle nor the other pioneers actually invented the gas turbine; the concept had been around for some time. Their genius lay in realis­ing that such an apparently unpromising and inefficient form of engine would provide the basis for high speed and high altitude flight.

Whittle filed his original jet-propulsion patent in 1930, and his experi­mental engine first ran in April 1937. Von Ohain’s records were lost during the war, but it is thought that a von Ohain/Heinkel engine actually ran in the previous month. This engine was however a preliminary experimental arrange­ment running on gaseous hydrogen.

The first jet-engined aircraft was the Heinkel He-178 shown in Fig. 6.17. Using a von Ohain engine, its maiden flight was on 27th August 1939, some 21 months before that of the British Gloster/Whittle E28/39.

Some gas turbines use a centrifugal compressor as shown in Fig. 6.18. This form was used on early British jet engines and is similar to the type used in superchargers. Air enters the rotating disc at the centre and is spun to the outside at increased pressure and a considerable whirl speed. A diffuser down­stream, consisting of fixed curved blades or passages, is used to slow the flow down by removing the whirl component. The reduction in speed is accom­panied by a further rise in pressure.

Both the Whittle and the von Ohain engines used a centrifugal compressor, but by 1939 rival British and German teams were already working on axial compressors which offer higher efficiency and reduced frontal area.

As shown in Fig. 6.19, an axial compressor consists of a series of multi – bladed fans separated by rows of similar-looking fixed stator blades. The mov­ing blades are used to increase the pressure and density rather than the speed. The stator blades remove the swirl and produce a further pressure rise.

The rise in pressure obtainable through a single row or stage is not as great as for a centrifugal compressor, and many stages are required. Despite a trend to higher overall pressure ratios, modern engines are able to use fewer stages because of improved design.

The earliest successful turbo-jet with an axial compressor was the Junkers Jumo 004 which was developed by a team led by the little-known Anselm Franz. In 1942 this engine was used to power the Messerschmitt Me 262, the

Centrifugal

compressor

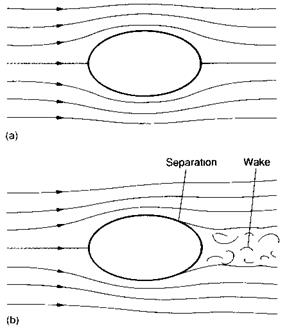
Fig. 6.20 A turbo-prop engine

The design illustrated uses centrifugal compressor stages. For turbo-prop engines, it is still common practice to use at least one centrifugal compressor stage.

The gearbox and accessory drives represent a significant proportion of the total engine weight (Illustration courtesy of Rolls-Royce pic)

world’s first jet-propelled combat aircraft (Fig. 2.18). The Jumo engine, with its axial compressor and annular combustion chamber, was much more like a modern engine than the Whittle or von Ohain engines, and was developed quite independently, with no knowledge of Whittle’s work.

Whittle’s heroic efforts are well documented in his book Jet (1953) and in a later book by Golley (1987). A full account of the early jet engines is given by Glyn Jones in The Jet Pioneers (1989).

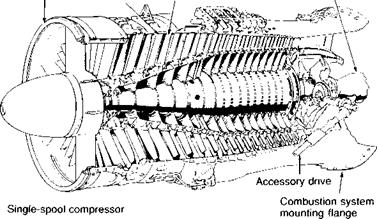
Although the axial compressor is always used for large turbo-jet engines, smaller engines and those designed for turbo-prop propulsion often have at least one centrifugal stage (see Fig. 6.20, and Fig. 6.21). The centrifugal compressor is simpler, and considerably cheaper than the axial type, and in applications such as helicopter propulsion, the increased diameter is of little significance.

When we consider rate of climb we are primarily concerned with increasing the potential energy of the aircraft as quickly as possible, and we will assume that we do not wish to change the forward speed at the same time so that the kinetic energy remains unaltered in the steady climb (Fig. 7.16).

Horizontal velocity

Rate of increase in potential energy
climb velocity x aircraft weight

Fig. 7.16 Rate of climb

Increased potential energy must be provided by excess engine power over that required for level flight

If we have a piston-engined aircraft, the required operating conditions are now quite clear. All we need to do is to make the difference between the power produced by the engine and the power required to overcome the drag as large as possible. This will provide the largest possible excess power to increase the aircraft potential energy at the highest possible rate (Fig. 7.17).

If we make the simplifying assumption that the engine power is constant, then we should operate at the forward speed corresponding to the minimum required power – the same speed that we found was required for maximum endurance in level flight.

For a turbo-jet engine, the power increases with speed and so we shall, once more need to compromise between the engine and airframe requirements. To get the maximum excess power we must operate at a speed in excess of the minimum required power speed (Fig. 7.18).

RATE OF CLIMB 211

Speed

Fig. 7.18 Maximum climb rate – jet engine

Because engine power increases with speed, maximum power for climb is obtained at a speed in excess of minimum power required speed and minimum drag speed

Unlike a car, an aircraft cannot be turned satisfactorily by means of the yaw control alone. This is because there is no road to provide a reaction to produce the cornering forces. In an aircraft, the cornering (centripetal) force must be provided by aerodynamic means. When the rudder is deflected so as to yaw the aircraft, the force that it produces is actually outwards; the opposite direction to that required.

As illustrated in Fig. 10.12, to execute a level turn properly, the aircraft must be banked, and the lift increased so that the horizontal component of lift is exactly the right size to provide the centripetal force required for the turn, and the vertical component exactly balances the weight. Normally a certain amount of rudder control is necessary in order to keep the aircraft pointing in the intended direction. Excessive use of the rudder, however, produces a skidding turn, with an uncomfortable sideways acceleration, and a potentially danger­ous sideslip.

vertical component of lift

Horizontal component of lift

Weight

Fig. 10.12 Turning flight

For a correctly banked turn, the lift force must be increased so that its vertical component exactly balances the weight. The horizontal component can then provide the required centripetal acceleration

The precise coupling between roll and yaw varies from one aircraft design to another. In general, a combination of aileron and rudder movement is required, but most aircraft can be turned smoothly using ailerons alone. Some early Farman aircraft had no rudder at all. The balance between rudder and aileron control also depends on whether the aircraft is climbing, descending, or flying level. A more detailed description will be found in practical flying manuals such as Birch and Bramson (1981).

Note, that once a properly executed turn has been initiated, the control stick or handlebars are returned to somewhere near the neutral or mid-position, and the aircraft keeps turning. Holding the stick over would cause the aircraft to continue rolling. This is quite different from steering a car, where the steering wheel must be held in the turned position.

One very special case where flat turns were necessary was in the man – powered Gossamer Albatross shown in Fig. 10.13. Because of its exceptionally low power, this aircraft required a high-aspect-ratio wing with a span similar to that of a large airliner, and could only fly close to the ground. In a banked turn the wing tip would be likely to hit the ground. The aircraft was therefore turned by means of the canard foreplane, which could be canted over so as to

produce a sideforce component to pull the nose round. Note that no fin or rud­der was provided.

As we explained in Chapter 4, in level flight, the contributions to drag from surface friction and normal pressure rise roughly as the square of the speed. The trailing vortex drag, however, decreases with speed, because the circula­tion, and lift coefficient required, decrease. In Fig. 4.21 we showed how the contributions to drag vary with speed. It was shown that the resulting total drag has a minimum value. The curve of resulting drag is repeated in Fig. 11.18. If we try to fly at a speed less than the minimum drag speed whilst trying to maintain a steady flight path then a decrease in speed will cause increased drag. The thrust of turbo-jet engines is not very sensitive to speed changes, so on jet – propelled aircraft the increase in drag will slow the aircraft down further. Similarly, a small increase in speed will result in less drag, so the aircraft will tend to fly even faster. Therefore, at speeds less than that for minimum drag, a turbo-jet aircraft suffers an instability of speed.

On piston-engined aircraft where the power is not greatly affected by the speed, a reduction in speed is usually accompanied by an increase in thrust, since power = thrust x speed. Up to a point, therefore, the increase in thrust

tends to compensate for the increase in drag, so piston-engined aircraft are less prone to speed instability.

There are also other reasons why turbo-jet aircraft are more prone to speed instability. When we looked at aircraft performance, we saw that the most eco­nomical flying speed is above the minimum-drag speed. For piston-engined air­craft, where the equivalent air speed (EAS) at cruise is only about two or three times as fast as the landing speed, the landing speed is normally fairly close to this minimum point. Any tendency to speed instability is, therefore, slight, and can be easily controlled by the pilot. For high speed turbo-jet aircraft, the cruis­ing (EAS) speed may be many times greater than the landing speed. Thus if the cruise is to be efficient, the landing speed will be well below the minimum drag speed, and speed instability becomes a more serious problem.

The problem of speed instability on turbo-jet aircraft is made worse by the fact that the response to throttle changes is much slower than for a piston – engined type. If the pilot of a turbo-jet propelled aircraft tried to flatten out and float down to a three-point landing, as was the custom in the piston-engine era, he might find himself taking-off again instead.

To solve the speed-instability problem, air brakes may be fitted as shown in Fig. 11.19. These devices increase the drag, and have the effect of pulling the minimum drag position point further to the left on the curve, as shown in Fig. 11.18. Flaps also help to increase the drag, and are normally deployed more fully for landing than for take-off. On Concorde an automatic throttle control system was used to help iron out the inherent speed instability at low speeds.

There are various methods of generating lift, as we shall describe, but we will start with the conventional wing.

In the conventional or classical aeroplane, each component serves one main function. The names and purposes of the principal components are shown in Fig. 1.3. In this classical configuration, nearly all of the lift is generated by the

provide directional

stability and control

Tailplane (honzontal stabiliser) provides stability and control

Fig. 1.3 The classical aeroplane

Each component serves only one main purpose wing. The tail, which is intended only for stability and control, normally pro­vides a slight negative lift or downforce.

Early attempts at aviation were often based on bird flight, where the flapping wing provides both the lift and the propulsive thrust. The classical arrangement (often attributed to the English engineer Cayley), provided a simpler approach that was better suited to the available technology. Some unconventional arrangements do have theoretical advantages, however, and because of advances in technology, they are becoming more common. On some recent aircraft types, the tail, and even the fuselage may contribute significantly to the lift, but we will deal with such departures later.

The amount of lift generated depends on the circulatory strength of the bound vortex, and on its length, which in turn depends on the span of the wing. A given amount of lift can be generated either by a short strong bound vortex, or a long weaker one. The longer weaker bound vortex will produce weaker trailing vortices, and as the downwash produced by the trailing vortices is responsible for the trailing vortex (induced) drag, the longer wing will produce less drag.

The longer the wing is, the weaker is the bound vortex required. For a given wing section and angle of attack, the strength of the bound vortex depends on the wing chord, so for a given amount of lift, the chord required reduces as the wing span is increased. Thus, wings designed to minimise trailing vortex (induced) drag, have a long span, with a small chord: in other words, the aspect ratio is high.

For a given wing section shape, any reduction in chord produces a corres­ponding reduction in depth. Therefore, as the aspect ratio is increased, it becomes more difficult to maintain adequate strength and stiffness.

Competition gliders or sailplanes often have wings with an extremely high aspect ratio, but for both structural and aerodynamic reasons, low aspect ratio wings are more suitable for very manoeuvrable aircraft such as the Hawk trainer shown in Fig. 9.2.

4^ СГ)

Fig. 2.9 High aspect ratio and large wing area were used on the Lockheed TR-1, which was designed for long range and endurance (Photo courtesy of Lockheed California Co.)

Because high aspect ratio wings have a good ratio of lift to drag, they are used on aircraft intended for long range or endurance. The aircraft shown in Fig. 2.9 is a good example. It is noticeable that long-range, high-endurance sea-birds also have high aspect ratio wings. The albatross has an aspect ratio of around 18. However, very low aspect ratio wings, such as those of Concorde, produce less drag in supersonic flight, as will be explained in later chapters.

Without the influence of viscosity, the streamlines or stream surfaces would close up neatly behind all parts of the aircraft, and there would be no wake. For a symmetrical shape such as that shown in Fig. 4.1, the streamline pattern and the pressure distribution would also be symmetrical, as in Fig. 4.1(a), and therefore, there would be no net resultant force. In fact, theoretical analysis shows, that if there were no viscosity, the pressure distribution would result in no net drag force on any shape. In the real case shown in Fig. 4.1(b), and Fig. 4.2, the streamline pattern and pressure distribution are not symmetrical, and a wake of slow-moving air is formed at the rear.

On shapes such as that shown in Fig. 4.1, the air pressure reaches its min­imum value at about the position of maximum section depth. Thus, over the tail portion, the air is flowing from a low pressure to a high one. As we have previously stated, this condition is known as an adverse pressure gradient, since the flow is likely to separate. Even if the flow does not separate, an adverse pressure gradient promotes a rapid degradation of available energy in the boundary layer, resulting in a reduction in pressure over the rear. Thus, on average, there is a lower pressure on the rear of the section than on the front, and therefore, there is now a net drag force, which is known as the boundary layer normal pressure (form) drag.

When the flow does separate, as illustrated in Fig. 4.1(b), the pressure down­stream of the separation positions is nearly uniform at a low value. Hence, the boundary layer normal pressure (form) drag will be high.

In general, the further forward the separation positions are, the greater will be the area of low pressure, and the higher will be the drag.

Note, that since there is a loss of available energy in the boundary layer, Bernoulli’s relationship does not apply there, as it is based on the assumption that the amount of available energy remains constant. In the boundary layer and the wake, the speed and the pressure can be simultaneously lower than in the free-stream values.

The term boundary layer drag (profile drag) is used to describe the combined effects of boundary layer normal pressure drag and surface friction drag. It is often convenient to combine these two forms of drag, as they both depend on the wing area and the dynamic pressure (l/2pV2). At constant altitude, both of these contributions to drag rise roughly with the square of the speed.

The propeller, the jet, and indeed all conventional aircraft propulsion systems involve changes in momentum of the air. When a change of momentum occurs, there must be a corresponding force, but it should not be thought that thrust is caused directly by the change of momentum, with no other mechanism being involved. As we have seen in the above examples, the force is produced and transmitted to the structure by pressure differences acting across the various sur­faces of the device. It is perhaps best not to think of rate of momentum change and force as cause and effect, but as two consequences of one process. In mak­ing practical measurements, or even theoretical estimates, we normally have to consider a combination of pressure-related forces and momentum changes.

Comparison between jet and propeller for thrust production

Figure 6.3 shows a jet aircraft and a propeller-driven one producing equal amounts of thrust at zero forward speed. In the case illustrated, the jet engine is transferring energy to the slipstream or jet five times as fast as the propeller. Since this energy must ultimately have come from the fuel, it indicates that the propeller-driven aircraft is producing the thrust more economically.

When the aircraft are in motion, the jet engine will still transfer energy to the air at a faster rate than the propeller at any given thrust and forward speed, but the difference in energy transfer rate becomes less marked as the speed increases.

The pure rocket will work at very high altitude and in the vacuum of space. The high speed of the exhaust gases and the added weight of the oxidant that must be carried, however, mean that it is extremely inefficient in comparison with air-breathing engines at low altitude.

The thrust of a rocket motor comes from the high pressure on the walls of the combustion chamber and exhaust nozzle. The same high pressure produces the acceleration and momentum change of the exhaust gases.

Rockets have been used to assist the take-off, and for experimental high altitude high speed research aircraft, but one production rocket aircraft was the Second World War swept tailless Messerschmitt Me 163. The motor used two chemicals, one of which was highly reactive and, if it did not explode during a

heavy landing, was liable to dissolve the occupant. It was reportedly unpopular with pilots!

One of the most obvious ways in which to satisfy the conflicting requirements imposed by a large speed range is to provide some mechanism to vary the sweep angle of the wing. Although this seems an attractive solution the mechanical problems faced in such a design are considerable. The hinge mechanism must clearly be at the root of the wing and this is the very position at which bending moment and structural demands will be greatest. Other important mechanical problems may be encountered such as the requirement to keep underwing stores, such as missiles or fuel tanks, aligned with the free stream direction as the sweep angle is changed on a military aircraft. It will also place restrictions on the positioning of the engines since wing mounting will clearly lead to severe complications.

In spite of these difficulties this solution has been employed on a number of aircraft, including the Tornado (Fig. 11.12), which was designed to fulfil a variety of roles from strike aircraft to high speed interceptor, and on the F-14 (Fig. 8.2). Both these aircraft are required to operate at high speed at low alti­tude. If the wing is operating at a relatively high loading then the increase in angle of attack due to an upwards gust will be less than that for a wing with a lower loading per unit area. This is because the more highly loaded wing will be operating at a greater angle of attack. A gust at a given flight speed will thus produce a smaller percentage change in angle of attack than it would for a wing operating at a reduced loading. This is a particularly important consideration for high speed low altitude operation and a swing-wing produces a suitable compromise.

Another method of sweep variation which has been proposed is to simply yaw the whole wing in flight as on the experimental NASA AD-1 shown in Fig. 8.16. This solution is not without its own complications, though, and some mechanical hinges may still be required (e. g. for any wing-mounted com­ponents, such as vertical stabilisers or at the wing fuselage junction). More­over the configuration is inherently asymmetrical in the swept configuration, and this is likely to lead to drag penalties because of the need for aerodynamic trim.