Wind, Body, Stability, and Principal Axes
One of the most distressing experiences for beginning stability and control engineers is to be faced with at least four alternate sets of reference axes for the equations of airplane motion. The original Bryan set, called body axes, is perhaps the most easily
|
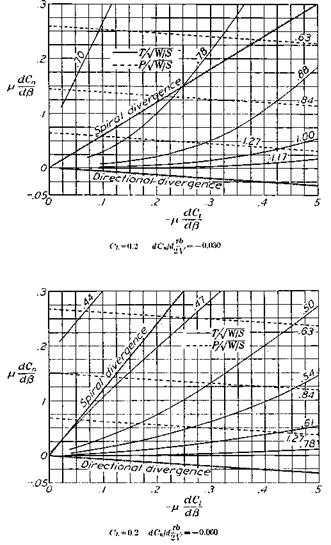
Figure 18.6 Representative lateral-directional stability boundaries. Spiral and directional divergence boundaries are given, along with approximations for Dutch Roll period and damping. The airplane relative density і is used in the chart coordinates. (From Zimmerman, NACA Rept. 589, 1937) |
grasped. Orthogonal reference axes are fixed in the airframe as if they were painted on, remaining in place through all subsequent motions. To be fair, even body axes can migrate with respect to the airframe, since the most common form has its origin at the airplane’s center of gravity, which shifts about with different loadings.
Body axes have the practical virtue that the variables of motion that are calculated, such as the linear and angular velocities, are easily related to the readings of flight instruments, which are, after all, also fixed to the body. However, in the early days of stability and control analysis, there were advantages to wind axes (Zimmerman, 1935).
In wind axes, the forward or X-axis points into the wind during the entire motion, rotating about the center of gravity with respect to the airframe. The independence of translatory and rotational motions allows this to happen without affecting the calculation of pitching motions. An advantage of wind axes is that the X and Z forces are the exact negatives of the familiar drag and lift forces presented in wind-tunnel test reports and used in airplane performance calculations.
Stability axes came into the picture in the 1940s, as a device to simplify calculation of small-perturbation airplane motions. Stability axes are a special set of body axes. The X stability axis points into the relative wind in the equilibrium flight that precedes the disturbed motion, but remains fixed in the body during the calculated motions around equilibrium. All that is accomplished by stability axes is the elimination of a few terms in the equations that include initial angle of attack. With the advent of powerful new digital computers stability axes have become mostly a curiosity, except for the fact that the primed derivatives mentioned in Sec. 2 have their basis in stability axes. Duane McRuer notes that
Primed derivatives based on stability axes often have a remarkably simple connection with the basic motions of the aircraft…. [For example] the square of the Dutch roll undamped natural frequency is usually given to a high degree of accuracy by N^…. stability axes are appropriate for determining the characteristic modes [of motion] and their predominant constituents.
To complicate things, the term stability axes sometimes has quite another meaning than that of a special set of body axes for flight dynamics studies. Wind-tunnel data are quite often produced in what are called stability axes, but for clarity should be named wind-tunnel stability axes. The Z-axis is in the plane of symmetry and normal to the relative wind; the X-axis is in the plane of symmetry and is normal to the Z-axis; the Y-axis is normal to both X – and Z-axes.
Principal axes are another curiosity in present-day practice, since they are used only to eliminate the product of inertia terms in the equations of motion. As with stability axes, principal axes have been obsoleted by powerful digital computers. A few added terms in the equations seem to add nothing to computing time.
The hybrid case in which wind axes are used for the three force equations and body axes for the three moment equations can be found in some simulations. The first hybrid application the authors are aware of was made by Robert W. Bratt at the Douglas Aircraft Company’s El Segundo Division, about 1955, in connection with inertial coupling studies. A more recent example of hybrid axes is NASA’s SIM2, which actually uses three sets of axes, wind, wind-tunnel stability, and body (Figure 18.7). SIM2 was first put to use at the NASA Dryden Flight Research Center for real-time digital simulation of the McDonnell Douglas F-15. The aerodynamic data base was filled in to an angle of attack of 90 degrees, to allow simulation of stalls and spins. Later SIM2 applications were to the space shuttle Orbiter and to the Northrop B-2 stealth bomber.
With three axes systems carried along simultaneously in the solution, the angular relationships among the SIM2 axes sets must also be continuously computed. The fundamental force vector equation on moving axes used in SIM2 uses the vector cross-product of angular velocity of wind axes and the velocity vector. A key vector equation solves for the angular velocity of wind axes as the angular velocity of body axes minus two terms, the angular velocity of wind-tunnel stability axes with respect to wind axes and the angular velocity of body axes with respect to wind-tunnel stability axes.
Wind axes differ from wind-tunnel stability axes only by a positive sideslip angle rotation about the Z stability axis, so that the second of the three terms in the vector equation for wind axes angular velocity has only one nonzero element, the sideslip angle rate. Likewise, wind-tunnel stability axes are derived from body axes by a single angle of attack rotation
along the negative Y-body axis. The required vector transformations are made in component form, always taking care to add components in the same axis systems.
The sideslip and angle of attack variables that define the difference among the three axis sets in SIM2 have one of the two possible definitions. The SIM2 convention happens to agree with the most common definition, in which wind axes are derived from body axes by an initial negative angle of attack – a rotation followed by a positive sideslip angle rotation в (Figure 18.8). The reverse convention is rare but not unknown.
Extended airplane axes sets that allow for flight at extreme speeds and altitudes, taking into account the earth’s actual shape, are treated in Sec. 15.