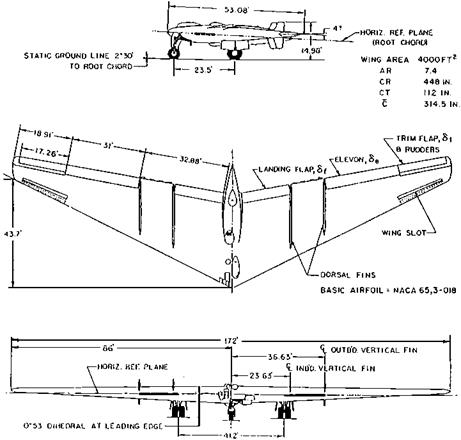
The Break with the Past
The 1947 NACA tail design requirements for satisfactory spin recovery stood relatively unchallenged until a series of NASA spin tunnel tests and some experiments at the Cessna Company in the late 1970s. Motivated somewhat by the Grumman/American AA-1B Yankee experience, NASA started a broad-based review of light airplane spin recovery. W. H. Phillips credits Joseph R. Chambers with initiating this work. The centerpiece of the program was a flight test fleet of four airplanes: a Cessna 172 Skyhawk, a modified Beech C23 Sundowner, a nonproduction Piper PA-28R T-tail Arrow, and a modified Yankee. Initial results from the review represent a distinct break with past NACA work, in particular, the 1947 TDPF tail design criterion. Nine tail configurations were tested on a model of the Yankee in the 20-foot Langley Spin Tunnel. Six of the nine designs were predicted to have satisfactory spin recovery characteristics according the 1947 TDPF criterion, yet only four showed satisfactory recovery in the spin tunnel (Burk, Bowman, and White, 1977). The investigators concluded:
On the basis of the results of the present investigation, the tail design criterion for light airplanes, which uses the tail damping factor (TDPF) as a parameter, cannot be used to predict spin recovery characteristics.
According to Burk, Bowman, and White, TDPF was intended to serve only as a conservative guideline for tail design, not as a criterion. Having made this decisive break with 30 years of stability and control design practice, the statement is softened somewhat in words that followed those quoted above, as follows:
However, certain principles implicit in the criterion are still valid and should be considered when designing a tail configuration for spin recovery. It is important to provide as much damping to the spin as possible (area under the horizontal tail), and it is especially important to provide as much exposed rudder area at spinning attitudes (unshielded rudder volume coefficient (URVC)) in order to provide a large antispin moment for recovery.
The real thrust of the NASA review of the 1970s lies in the investigation of factors for light-plane spin recovery other than tail design. The NASA and contractor investigators, including H. Paul Stough III, William Bihrle, Jr., James M. Patton, Jr., Steven M. Sliwa, Joseph Chambers, and Billy Barnhart, found that wing and aft fuselage design details affected the results in ways that cannot be ignored. According to John C. Gibson, British spin tests in the 1930s had already disclosed the importance of rear fuselage design.
The evidence on fuselage aft details is not completely clear, because it is bound up in scale effects, or Reynolds number. Side forces, contributing to damping, of square or rectangular fuselage cross-sections appear to be particularly sensitive to Reynolds number. Thus, results from small-scale spin model tests that pin flat, unrecoverable spins to flat-bottomed rear fuselages (Beaurain, 1977) must be considered only tentative. On the other hand, the recent NASA findings on wing design effects on spins are conclusive and important, as detailed in a following section.
Having seen the NASA spin experts make a decisive break with the past, represented by NACA 1946 and 1947 tail design criteria, what advice can one give to designers of new general-aviation airplanes? Well-funded military programs present no problem, since modern spin testing techniques, such as drop models and rotary-balance tests, that are recommended by NASA are available to them. The concern is with light-airplane designers who have been cast adrift, so to speak, with NASA’s abandonment of the TDPF design criteria.
The most reasonable course to take for designers of new light airplanes who have no budget for extensive spin model testing probably is as follows:
1. Follow the 1947 TDPF criteria. The evidence is that the criteria deal with the right design details, even if the numerical values are incorrect in some cases because of the influence of other parameters.
2. Avoid the design details that are implicated in flat, unrecoverable spins: flat – bottomed rear fuselages and wings with full-span leading-edge droop.
3. Design the outer wing panels to be able to accommodate a drooped leading edge, if spin problems appear during flight test.
4. Check with NASA on the possibility of doing spin tunnel, rotary balance, or model drop tests for the new design. NASA is able to consider such tests if the results would be of general scientific interest, covering new ground.