A mathematical model of the earth’s atmosphere is needed for stability and control flight simulation and other computer programs. These programs typically use dimensionless stability derivatives in setting up equations of motion for flight dynamics studies, and stability augmenter and autopilot analyses.
Standard atmospheric mathematical models were published by NACA starting in 1932. A 1955 model covered altitudes up to 65,800 feet (ICAO, 1955). NACA, the U. S. Air Force, and the U. S. Weather Bureau extended that model to an altitude of 400,000 feet (ICAO, 1962). The AIAA publishes a guide to standard atmosphere models (1996). For all its utility, the standard atmospheric model is based on quite simple assumptions: The air is dry, it obeys the perfect gas law, and it is in hydrostatic equilibrium.
Standard atmosphere computer codes for stability and control computer programs normally accept as inputs the airplane’s altitude and true speed at each computing time. A minimum set of outputs at each computing time would include atmospheric density, Mach number, dynamic pressure, and equivalent airspeed. Additional outputs that could be generated are static pressure and calibrated airspeed.
The standard atmosphere FORTRAN computer code shown in Figure 18.10 represents one of the two methods used in stability and control programs. In this example, air density (RHO) is curve-fitted with exponential functions. Four function fits give satisfactory accuracy over the entire range of -4,000 to 400,000 feet. Speed of sound (ASPE), from which the Mach number is calculated, requires eight curve-fitted linear equations. The alternate standard atmosphere coding is ordinary interpolation from stored tables of density and speed of sound.
It has become increasingly important to represent wind gusts, shears, downbursts, and vortex encounters in stability and control flight simulation. Early flight simulations relied on a very simplified approach in which an additional gust angle of attack or sideslip is simply added to the values calculated at each instant from the airplane’s motions in an inertial space reference.
The sounder approach, now in common use, is an inertially fixed model for the wind environment, including gusts, shears, downbursts, and vortices. A NASA downburst model uses the conservation of mass principle to calculate wind velocity at all points within a down – burst (Bray, 1984). A central core is surrounded by an annular mixing region and a region of outflow parallel to the ground (Figure 18.11). In the Bray inertially fixed wind environment, an airplane penetrates the wind model as it moves along its path, just as in reality.
Earlier ad hoc wind shear models were proposed by NASA for flight simulation. A boundary layer shear model represents a low-level temperature inversion overlaid by strong winds. Two additional shear models, with the colorful names of the Logan and Kennedy shears, represent meteorologists’ best estimates of conditions existing at those airports during specific airplane wind shear encounters.
In Bernard Etkin’s terminology, the Bray downburst model and the NASA shear models are usually used as point atmospheric models, in which variations of local wind velocity over the airplane’s dimensions are neglected. Otherwise stated, the airplane is assumed to be vanishingly small with respect to the wavelengths of all spectral components in the turbulent atmosphere. This assumption obviously fails for gust alleviation systems that depend on sensing devices that sample air turbulence ahead of the main structure.
Etkin (1972) provides a thorough study of the finite airplane case, in which local wind velocities vary over the airplane’s dimensions. The required mathematics are surprisingly complex because atmospheric turbulence is a random process, and only a statistical, probabilistic
SUBROUTINE ATMOS (ALT, VEL, R HO, AMACH, DYN, VEKT)
: NASA/USAF/USWB STANDARD ATMOSPHERE, -4,000 TO 400,000 FT. DIMENSION X(3)
X(3) = ALT
IF(-X(3)-35.E3) 300,300,310 300 Z1 = 342.5E2 + X(3)*4.3/35.
GO TO 500
310 IF(-X(3)-45.E3)320,320,400 320 Z1 = 299.5E2-.285*(-X(3)-35.E3)
GO TO 500
400 IF(-X(3)-60.E3) 405,405,410 405 Z1 =271 .E2-.1 2*(-X(3)-45.E3)
500 RHO = .002377*EXP(X(3)/Z1)
GO TO 490
410 IF(-X(3)-140.E3) 415,415,420
415 RHO = EXP(-4.67263E-5*(-X(3)-6.E4)-8.41 364)
GO TO 490
420 IF(-X(3)-240.E3) 425,425,430
425 RHO = EXP(-3.871 2E-5*(-X(3)-14.E4)-1 2.1 51 584)
GO TO 490
430 RHO = EXP(-5.18378E-5*(-X(3)-24.E4)-16.022785)
490 CONTINUE
IF(-X(3)-362.E2)600,600,700 600 ASPE = 1117.-149.*(-X(3)/362.E2)
GO TO 800
700 IF(-X(3)-66.E3) 710,710,720 710 ASPE = 968.
GO TO 800
720 IF(-X(3)-105.E3) 730,730,740
730 ASPE = 6.71 282E-4*(-X(3)-66.E3) + 968.
GO TO 800
740 IF(-X(3)-1 555.E2) 750,750,760 750 ASPE = 1.73941 E-3*(-X(3)-105.E3) + 994.1 8 GO TO 800
760 IF(-X(3)-1 72.E3) 770,770,775 770 ASPE = 1082.02 GO TO 800
775 IF(-X(3)-200.E3) 780,780,785 780 ASPE = -1.21 5714E-3*(-X(3)-1 72.E3) + 1082.02 GO TO 800
785 IF(-X(3)-2625.E2) 790,790,795 790 ASPE = -2.6 236 8E-3*(-X(3)-200.E3) + 1047.98 GO TO 800 795 ASPE = 884.
800 AMACH =VEL/ASPE DYN = (RHO/2.)*VEL* *2 VEKT = 1 7.1 861 21 6*SQRT(DYN)
RETURN
END
Figure 18.10 FORTRAN digital computer subroutine for the NASA/USAF/USWB standard atmosphere. Air density (RHO) and speed of sound (ASPE) are curve-fitted in altitude bands from -4,000 to 400,000 feet. The subroutine requires inputs of altitude (ALT) and true speed (VEL). The subroutine outputs density, Mach number (AMACH), dynamic pressure (DYN), and equivalent airspeed (VEKT). (From ACA Systems, Inc. FLIGHT program)
treatment can be made (Ribner, 1956). Local wind velocity is a random function of both space and time. It simplifies things to assume stationarity, homogeneity, isotropy, and Gaussian distributions. Experimental data exist that provide adequate turbulence models for both high altitudes and near the ground, where isotropy does not hold.
More exotic atmospheric disturbances are significant for operation at very high altitudes and at hypersonic speeds. Flight disturbances due to temperature shears experienced by the
|
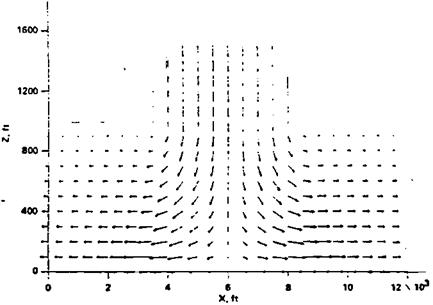
Figure 18.11 Vertical cross-section through the Bray model of a down-burst. Arrow lengths are proportional to air flow velocity. (From Bray, NASA TM 85969, 1984)
|
Lockheed SR-71A and the North American XB-70 are discussed in Chapter 11, “High Mach Number Difficulties.” In anticipation of a National Aerospace Plane (NASP) that would fly hypersonically, NASA laboratories at Dryden, Marshall, and Langley and the McDonnell Douglas Houston operation collaborated on a sophisticated FORTRAN atmospheric model called the NASP Integrated Atmospheric Model (Schilling, Pickett, and Aubertin, 1993).
The model is suitable for real-time simulations as well as batch programs. It provides global coverage, from the ground to orbital altitudes. The NASP model features of particular stability and control interest are the small-scale perturbations that include continuous turbulence and the “thermodynamic” perturbations of density, pressure, and temperature. Gusts and thermodynamic perturbations can be selected either in patches or as discrete upsets.
Isolated mountain ridges that lie at right angles to the direction of strong prevailing winds can generate a so-called mountain wave. Air over the top of such a ridge cascades in huge volumes onto the lower terrain to the leeward. It then seems to bounce off, rising, then falling, and then rising again in a series of diminishing waves, all parallel to the ridge line. A huge rotor, or horizontal vortex, forms to the leeward of the first bounce. The characteristic mountain wave structure is well known to glider pilots, since glider altitude records are set by maneuvering into the rising air of the first bounce. Glider pilots also know to avoid the rotor, whose lower edge generally just brushes ground level. The National Transportation Safety Board (NTSB) concluded that a rotor was a possible cause for at least one airline accident. This was United Airlines Flight 585, a Boeing 737 lost at Colorado Springs in 1991. Various jet aircraft encounters with a rotor are modeled by Spilman and Stengel (1995).
Vortex wakes left in the atmosphere by airplanes flying ahead can be a severe hazard, although the principles for avoiding vortex wakes are known. Vortex wake fields can be modeled for flight simulation (Johnson, Teper, and Rediess, 1974).












