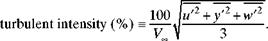A fully developed turbulent boundary layer is a region of large-scale velocity fluctuations (i. e., up to 10 percent fluctuations about a mean value). The flow is chaotic and irregular. Thus, although the external mean flow at the outer edge of the boundary layer is steady, the boundary-layer flow is unsteady. There is no chance—even with modern computers—of being able to predict the turbulent-flow behavior at a fixed point in the boundary layer as a function of time. However, experiments have shown that the turbulent fluctuations in the boundary layer are random, so that a time – averaged approach may be used. Thus, we focus on being able to predict what happens “on the average” at a point within the turbulent boundary layer. As in the laminar-boundary-layer problem, our goal is to be able to predict the growth and velocity profile of an incompressible, turbulent boundary layer. To accomplish this, the first step is to derive the appropriate differential equations and then seek solutions for them.
Time-Averaged Boundary-Layer Equations
We could begin by developing the time-averaged Navier-Stokes equations and then apply the boundary-layer approximations (i. e., d/x << 1, and so on). However, we choose instead to derive the time-averaged, boundary-layer equations of continuity and momentum directly from the laminar-boundary-layer equations. As before, we use an airfoil coordinate system (x, y, z), where x is the streamwise direction, y is the transverse direction, and z is normal to the surface. Based on experimental measurements, it is assumed that the turbulent flow is characterized by random fluctuations about a mean. Thus, we let:
U = U + u’; V = V + v’; W = W + w’, (8.120)
where:
U ^ instantaneous velocity
U ^ mean velocity
u’ ^ turbulent fluctuation,
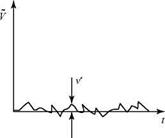
and so on. Now, if a fast-response instrument were used to measure the instantaneous velocity components at a fixed point in a two-dimensional boundary layer, the output would look like Fig. 8.32, which recognizes that in a two-dimensional flow, the transverse mean velocity, V, is zero (although the fluctuations in the transverse direction are not).
Because the velocity fluctuations are random, a mean-velocity component in any direction may be defined as the integral of the instantaneous velocity component over a time interval t = T, where T is a long-enough interval so that the value of the integral is independent of time. Thus,
U = — J Udt and U = – J u ‘dt = 0, (8.121)
T 0 T 0
 w
w
t
W
jL
where the bar over the u’ denotes a time average. Likewise, V = 0 and W = 0 These equations are stating that, because there is an equal likelihood that U is positive or negative at any instant, a summing of the value of U over a long time interval T is zero. However, the time average of the squares of the velocity fluctuations (to appear later in the boundary-layer equations) is not zero; in fact, it is positive. This follows if we imagine that at each instant of time, the value of u is measured and the value squared. Whether u’ is instantaneously positive or negative, the square is positive and the sum of the squared quantities over time is not be zero. Thus,
Be careful when writing (or reading) the time-averaged notation. Thus,
u’2 Ф u’2.
The time average of the cross-products of velocity fluctuations in general is not zero. However, in a two-dimensional boundary layer:
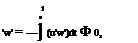 T
T
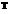 (8.123)
(8.123)
0 (a fact that is needed later), whereas:
u’v’ = v’ w’ = 0.
Before proceeding to time-average the defining boundary-layer equations, the following rules are needed, which follow from the definition of mean value. If A is a mean quantity, a and b are fluctuating quantities, and t is any Cartesian or time coordinate, then:
___ — t — T
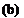
Aa = t j (Aa)dt = (A t j (a)dt = Aa.
We proceed now to substitute instantaneous velocity components into the laminar boundary-layer equations for continuity and x-momentum, Eq. 8.37, with the steady – flow velocity components (u, w) in Eq. 8.37 replaced by the instantaneous velocity components (U, W). Because the flow now is unsteady, a d/dt term must be added to the steady-flow momentum equation in Eq. 8.37. If the velocity field within the boundary layer is unsteady, then pressure fluctuations must exist as well. Thus, we also replace the steady pressure p by the instantaneous pressure p = P + p’, where P is the mean value of the pressure and p’ is the pressure fluctuation. As with the velocity fluctuations, p’ = 0 . Finally, because the flow is incompressible, r = constant. Then, Eq. 8.37 becomes:
We now time-average these two equations over a suitably long time interval T so that the equations reflect what is happening in the boundary layer on the average. The process begins by taking the average of both sides of each equation; that is, Eqs. 8.118 and 8.120 are rewritten with an overbar above each side. Then, by appealing to Eq. 8.117a, the two sides are expanded and then decomposed into the time average of each term. Thus,
the control volume (left side) is equal to the net pressure and viscous forces acting on the control surface (right side). In this equation, the time-averaged momentum flux is that due to mean velocity (first term on the left side) and fluctuating velocities (second term on the left side). Now, say that there is a change in the pressure and viscous forces that leads to an increase in overall momentum flux. Any corresponding increase in the momentum flux due to velocity fluctuations must reduce the effect of the force change on the time-averaged momentum flux due to the mean velocities. Thus, the turbulence term has the same role as a stress; namely, it tends to extract momentum associated with the mean flow. The turbulence-momentum term in Eq. 8.124 then is moved conventionally to the other side of the equation and considered as a stress. It is called an apparent stress or a Reynolds stress. Be careful: The term (ри’и/) is physically not a stress; however, mathematically, it is considered to play the role of a stress. The term (pu’w’) is an apparent shear stress. The term
(ри2) neglected in Eq. 8.12 is an apparent normal stress. As in the molecular – viscosity case studied previously, the apparent normal stress is negligible compared to the apparent shear stress.
Rewriting Eq. 8.121 and moving the apparent shear-stress term in Eq. 8.124 to the right side, the turbulent boundary-layer equations are:
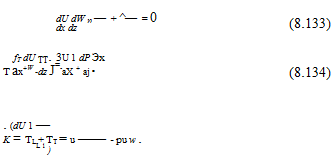 where:
where:
In turbulent flows, tt >> tl, except near the surface, where tt approaches zero.
Inspection of Eqs. 8.125 and 8.126 shows that the solution of these equations is problematic. There now is an extra unknown, pu’ w’, with no information on how to find it. Unfortunately, it is not a property of the fluid but rather a property of the turbulence. Hence, we expect this unknown to have different values within the boundary layer (Fig. 8.33) and also for different turbulent shear flows (e. g., for a boundary-layer flow and for a free-shear layer). Specifying the turbulent-shear – stress term is called the closure problem, meaning that it must be modeled empirically. This is discussed, when solutions are addressed.
A final comment on the turbulent boundary layer: The mean turbulent kinetic energy per unit volume in the boundary layer is defined as:
Large-scale eddies in the boundary layer extract kinetic energy from the freestream. This kinetic energy becomes increasingly more randomly distributed as it is transferred to increasingly smaller eddies. Ultimately, it is dissipated as thermal energy (i. e., heat) at the molecular level.
У
 s
s
The quality of the freestream flow in a “low-turbulence” wind tunnel often is defined as the magnitude of the freestream turbulent intensity,
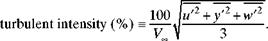

(8.136)
If a wind tunnel is to be used for turbulence research, the turbulent intensity of the
freestream flow in the test section should be only a few hundredths of 1 percent.














 w
w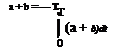
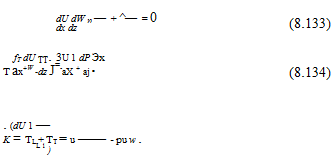 where:
where: