Category Basics of Aero – thermodynamics

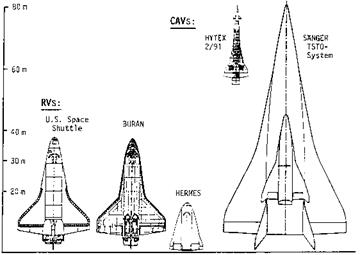
In the following chapters we refer to RV-type and CAV-type flight vehi­cles as reference vehicles. They represent the two principle vehicle classes on which we—regarding the basics of aerothermodynamics—focus our attention. ARV’s combine their partly contradicting configurational demands, whereas AOTV’s are at the fringe of our interest. Typical shapes of some RV’s and CAV’s are shown in Fig. 1.2.

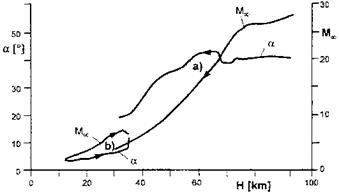
Characteristic flight Mach number and angle of attack ranges as function of the altitude of the Space Shuttle Orbiter, [15], and the SANGER TSTO space-transportation system, [16], up to stage separation are given in Fig. 1.3. (Basic trajectory considerations can be found in [5].) During the re-entry flight of the Space Shuttle Orbiter the angle of attack initially is approxi­mately a = 40° and then remains larger than a = 20° down to H « 35 km, where the Mach number is Ыж « 5. SANGER on the other hand has an angle of attack below a = 10° before the stage separation at Ыж « 7 occurs.

The ranges of the flight altitude H, the flight Mach-number MTO, and the angle of attack a, together with a number of other vehicle features govern the

aerothermodynamic phenomena found at a hypersonic flight vehicle. We give an overview of these features together with some of the resulting typical flow features in Table 1.2 on page 9. The considered vehicles are the Space Shuttle (SS) Orbiter and the lower stage (LS) of SANGER, each at a characteristic trajectory point.

Regarding the flow features we look only at some of them found along the lower symmetry lines of the two vehicles. Apart from the nose region and the

beginning of the boattailing (x/L = 0.82), the lower (windward) symmetry line of the Space Shuttle (SS) Orbiter has no longitudinal curvature. (The lower side of the vehicle is mostly flat at 0.12 ^ x/L ^ 0.82, see, e. g., [5].) At the lower stage (LS) of SANGER we consider only the forebody up to the location of the beginning of the inlets of the propulsion system [5]. The lower side actually is a pre-compression ramp for the inlets. Apart from the nose region it is flat.

Vehicle surface properties We note first that the lower side of the SS Or­biter has, except for the nose region, a rough surface, given by the tiles and the gaps between them of the thermal protection system (TPS). The SANGER LS has a smooth surface. This is a necessity—regardless of the structure and materials concept of the vehicle—because the boundary layer must not be in­fluenced negatively by the surface properties (permissible surface properties, Section 1.3).

Aerothermoelasticity Both the static and the dynamic aerothermoelastic – ity are important flight vehicle issues. For the SS Orbiter generally it can be stated that surface deformations are of such a small magnitude that the flow field past it is not affected. The situation is different at the SANGER LS forebody. There temperature differences exist between the lower and the upper side, Section 7.3. These differences may lead to a static deformation of the approximately 55 m long forebody with large consequences for the flow, in particular the inlet-onset flow, the thrust of the propulsion system and the aerodynamic forces and moments of the vehicle [5]. The same holds for the dynamic deformation of the forebody.

Atmospheric fluctuations are not of influence for the SS Orbiter on its high trajectory elements. There density uncertainties are a matter of con­cern, Section 2.1. Below 60 to 40 km altitude atmospheric fluctuations have an influence on the laminar-turbulent transition process. This holds for the Orbiter, but in particular for the SANGER LS, which flies at most at 33 km altitude. At the Orbiter the thermal loads are affected by the laminar – turbulent transition, whereas the drag increase does not matter.

Surface radiation cooling of external surfaces reduces the thermal loads to a degree that re-usable thermal protection systems (RV’s) and hot primary structures (CAV’s, partly found also at RV’s), become possible at all, Chapter 3. The external surfaces of both the considered vehicles are radiation cooled, the SS Orbiter, however, only at the surface portions which are exposed to the free stream (windward side). The in Table 1.2 given emissivity coefficients (necessary surface properties, Section 1.3) are nominal ones. The real ones are of that order of magnitude. At non-convex surface portions, the (fictitious) emissivity coefficient is smaller, Sub-Section 3.2.5.

High-temperature real-gas effects are present in both the inviscid and the viscous flow field past the windward side of the SS Orbiter. They are due to the high total enthalpy and the strong compression of the air stream at the vehicle surface. In Fig. 2.4 it is indicated—although the here considered trajectory point lies just outside of the graph—that

chemical non-equilibrium of the major constituents of air is present. Ac­cordingly catalytic surface recombination is possible, Sub-Section 4.3.3, if the related permissible surface properties, Section 1.3, are exceeded. Then also heat transfer due to mass diffusion happens, in addition to the anyway present molecular heat transfer, Sub-Section 4.3.3.

At the SANGER LS high-temperature real-gas effects are small, Fig. 2.4. The total enthalpy of the free-stream in this case is much smaller than in the SS Orbiter case. Nevertheless, vibration excitation of O2 and N2 is present and—at most weak—dissociation of O2. Hence surface catalytic recombina­tion is not a topic and also not heat transfer by mass diffusion.

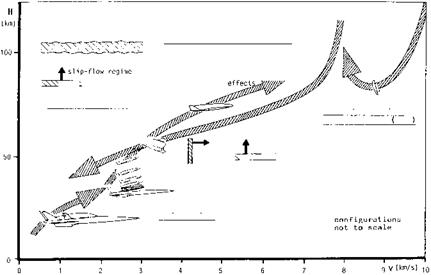
Low-density effects The Knudsen numbers for the two flight vehicles at the given trajectory points are such that no low-density effects occur, Fig. 2.6. Possible exceptions are air data gauges and measurement orifices.

Entropy layer The SS Orbiter has a blunt nose region and the SANGER LS a blunt nose. At a blunt configuration at supersonic or hypersonic flight speed due to the curved bow-shock surface an entropy layer appears, Sub­Section 6.4.2. At a symmetric body at zero angle of attack it has a shape which resembles a slip-flow boundary-layer profile (see Fig. 9.26 on page 370), the symmetric case in Fig. 6.22. In the asymmetric case a wake-like entropy layer appears, at least around the lower symmetry plane [5]. In our cases this situation is given. Entropy-layer swallowing must be taken into account in boundary-layer computation schemes and it plays a role in laminar-turbulent transition.

Flow three-dimensionality Above we have noted the geometrical situation along the lower symmetry lines of the two vehicles. Hence boundary-layer flow three-dimensionality is present at the SS Orbiter in the nose region and in down-stream direction for x/L ^ 0.12. At the SANGER LS the flow on purpose is two-dimensional at the lower side of the forebody (inlet onset flow [5]), Fig. 7.8.

Laminar-turbulent transition does not happen at the SS Orbiter at the considered trajectory point. The unit Reynolds number is much too low there, upper left part of Fig. 2.3. However, at deflected trim or control surfaces transition-like phenomena might appear. At the Orbiter striation heating was observed at the body flap, possibly due to Gortler instability, Sub-Section 8.2.8. Further down on the trajectory, where the unit Reynolds number be­comes large, of course laminar-turbulent transition happens. At 45 km alti­tude it happens at the lower side already at about 30 per cent vehicle length, Fig. 3.3. At the other surface portions it will happen further down on the trajectory. Due to the TPS tile surface at the SS Orbiter lower side, transition there is roughness-dominated, Sub-Section 8.3.1.

At the SANGER LS laminar-turbulent transition in any case happens, due to the low flight altitude. The prediction of the shape and the location of the transition zone today still is not possible to the needed degree of accuracy. At the upper side of the forebody transition will occur further downstream than at the lower side. One of the reasons is that at the upper side the unit

Reynolds number is approximately only one third of that at the lower side. The lower side is a pre-compression surface for the inlets, whereas the upper side is more or less a free-stream surface.[7] The SANGER LS is an aircraft-like flight vehicle and definitely transition sensitive, Chapter 8.

Boundary-layer edge Mach number The windward side boundary layer at the SS Orbiter at large angle of attack initially is a subsonic, then a transonic, and finally a low supersonic, however, not ordinary boundary layer. During re-entry one has typically at maximum Me « 2.3, and mostly Me ^ 2 [19]. This is in contrast to the boundary layer at the lower side of the SANGER LS. There a true hypersonic boundary layer exists with appreciably high edge Mach numbers.

Boundary-layer edge temperature The boundary-layer edge flow at the SS Orbiter is characterized by very large temperatures and hence high- temperature real-gas effects. The given boundary-layer edge temperature at the stagnation point is guessed to be approximately 9,000 K from Fig. 2.3. Assuming for the expansion to Me = 2,3 an effective ratio of the specific heats Yeff = 1.14, [20], we arrive at T « 6,500 K at the beginning of the boattailing.

At the SANGER LS due to the flight at small angle at attack, no large compression effects occur. We find them only in the blunt nose region and possibly at (swept) leading edges, inlet ramps and trim and control surfaces [5]. Hence the boundary-layer edge temperatures are moderate to low and the rather mild high-temperature real-gas effects are essentially restricted to these configuration parts and to the boundary layers.

Wall temperature The radiation cooling of the vehicle surfaces is very effective. This holds in particular for the SS Orbiter due to the small unit Reynolds number at the large altitude, the large surface curvature radii at the stagnation-point region and the then more or less flat surface. The radia­tion cooling at the SANGER LS would reduce the surface temperature even down to approximately 500 K, if the boundary layer would remain laminar, Section 7.3. Actually laminar-turbulent transition occurs with a subsequent rise of the wall temperature level to about 1,000 K. At the vehicle’s nose the contradictory demands of minimization of wave drag and wall temperature exist. The first demand asks for small nose radii and the latter for large ones. The reader is referred in this regard to, e. g., [5, 21]. We note also that the radiation-adiabatic temperature Tra in general is a good approximation of the actual wall temperature Tw, Chapter 3.

Boundary-layer temperature and density gradients Due the rather low surface temperatures because of the radiation cooling, strong wall-normal temperature gradients are found at the SS Orbiter. At the SANGER LS medium gradients are present for laminar flow and large ones for turbulent flow. Note that the resulting heat fluxes in the gas at the wall qgw are not the heat fluxes qw which enter the surface of the TPS or the hot primary

structure. In general we have qw ^ qgw because of the large amount of heat qrad radiated away from the surface, Chapter 3. Because at both flight vehicles the attached viscous flow to a good approximation is a first-order boundary – layer flow, the density gradients are inverse to the temperature gradients [22].

Thermal surface effects—viscous At the SS Orbiter viscous thermal sur­face effects, Section 1.4, are negligible except to a certain degree at the de­flected trim and control surfaces as well as at the thrusters of the reaction control system [5]. This is in stark contrast to the SANGER LS, where viscous thermal surface effects are of utmost importance. In this regard a number of examples is given in several chapters and in particular in Chapter 10.

Thermal surface effects—thermo-chemical These effects concern mainly surface catalytic recombination at the SS Orbiter due to the very hot bound­ary layer and the resulting thermo-chemical non-equilibrium of the flow, see also Chapter 10.

Basics of Aerothermodynamics

Ernst Heinrich Hirschel

The last decade has seen the successful performance at hypersonic speed of ramjet and scramjet propulsion systems. This probably is the true dawn of airbreathing hypersonic flight. In any case, these recent accomplishments are the motivation to emphasize the importance of viscous effects in this second edition of the Basics of Aerothermodynamics.

The flow past airbreathing hypersonic flight vehicles is viscosity-effects dominated. These effects concern the viscous drag (a large part of the to­tal drag), the integrated aerothermodynamic airframe/propulsion flow path including the engine’s air inlets and nozzles, and the performance of aero­dynamic trim, stabilization and control surfaces. In the flow past re-entry vehicles viscous effects are mainly important at trim and control surfaces. The viscous drag there—on a large part of the re-entry trajectory—is only a small part of the total drag.

In view of vehicle design and development an important aspect needs to be considered. The surface of the external flow path of an hypersonic vehicle of any kind is mainly surface-radiation cooled, at very high Mach numbers in particular cases also actively cooled. The ensuing wall temperatures and heat fluxes in the gas at the wall—the thermal state of the wall—are variable all over the vehicle’s surface. Many flow phenomena including laminar-turbulent transition depend strongly on the thermal state of the wall—thermal surface effects. The thermal state of the surface in turn depends strongly on the state of the boundary layer, laminar, transitional, or turbulent.

The problem is that today the flow simulation in ground facilities of any type does not allow to take into account the thermal state of the surface of a complete flight vehicle model. This also holds for hot model surfaces which are not radiation cooled. The hot experimental technique is in its infancies. How far it can be developed, is an open question. Of course, the discrete numerical methods of aerothermodynamics are on the rise. But for quite a time to come the computational simulation will not take over completely the tasks of the ground-facility simulation. This holds for the verification of the aerodynamic shape design as well as for the generation of the aerothermodynamic data set.

The first edition of the Basics of Aerothermodynamics had already as focus—besides that on the classical gasdynamic and thermodynamic
phenomena—that on the viscous phenomena in high-speed flow. And this in view of the fact that external vehicle surfaces are radiation cooled.

In this second edition the chapters with the classical topics remain ba­sically untouched. The accessibility to some single topics is improved. The sections and chapters devoted to viscous effects are, as before, complemented with the discussion of thermal surface effects, partly however in more detail. A final chapter is added, which is completely devoted to recent results regard­ing thermal surface effects from both theoretical/numerical and experimental investigations.

The author hopes that in this way the knowledge is enhanced about vis­cous effects in the flow past hypersonic flight vehicles. This holds in particular for airbreathing vehicles, but also for re-entry vehicles. Hypersonic glide vehi­cles have the same design problems as airbreathing vehicles, however without the particularities of the propulsion system’s integration.

The aim of the book is to convey to the student a broad knowledge of all aspects of aerothermodynamics, in particular also of viscous effects. The vehicle designer in addition should become aware of where these effects are important and how they are to be quantified and simulated. This holds for both ground facility and computational simulation.

Ernst Heinrich Hirschel

This second edition of the book benefits from the input of several colleagues. The author is very much indebted to S. P. Schneider, who freely provided information about recent work and results on laminar-turbulent transition. The same holds for R. Radespiel, for G. Simeonides, and for S. Hein. The latter also checked Chapter 8. R. Friedrich, Ch. Mundt, and G. Simeonides gave very welcome advice and also material regarding several topics.

Decisive for Chapter 10 was the illustrative material provided by M. Frey, A. Gulhan and S. Willems, T. Neuenhahn, H. Olivier and M. Bleilebens, and C. Weiland and J. Haberle. The chapter lives from their results, which partly were only recently obtained. This holds also for illustrative material provided for Section 9.1 by V. Statnikov, J.-H. Meiss, M. Meinke, and W. Schroder. I am very grateful to all of them.

Finally I wish to thank C. Weiland, who did the proofreading of the chapters and sections with new material.

Last not least, special thanks go to my wife for her support and her again never exhausted patience.

Ernst Heinrich Hirschel

The last two decades have brought two important developments for aerother – modynamics. One is that airbreathing hypersonic flight became the topic of technology programmes and extended system studies. The other is the emergence and maturing of the discrete numerical methods of aerodynam- ics/aerothermodynamics complementary to the ground-simulation facilities, with the in parallel enormous growth of computer power.

Airbreathing hypersonic flight vehicles are, in contrast to aeroassisted re-entry vehicles, drag sensitive. They have, further, highly integrated lift and propulsion systems. This means that viscous effects, like boundary-layer development, laminar-turbulent transition, to a certain degree also strong interaction phenomena, are much more important for such vehicles than for re-entry vehicles. This holds also for the thermal state of the surface and thermal surface effects, concerning viscous and thermo-chemical phenomena (more important for re-entry vehicles) at and near the wall.

The discrete numerical methods of aerodynamics/aerothermodynamics permit now—what was twenty years ago not imaginable—the simulation of high speed flows past real flight vehicle configurations with thermo-chemical and viscous effects, the description of the latter being still handicapped by in­sufficient flow-physics models. The benefits of numerical simulation for flight vehicle design are enormous: much improved aerodynamic shape definition and optimization, provision of accurate and reliable aerodynamic data, and highly accurate determination of thermal and mechanical loads. Truly multi­disciplinary design and optimization methods regarding the layout of thermal protection systems, all kinds of aeroservoelasticity problems of the airframe, etc., begin now to emerge.

In this book the basics of aerothermodynamics are treated, while trying to take into account the two mentioned developments. According to the first development, two major flight-vehicle classes are defined, pure aeroassisted re-entry vehicles at the one end, and airbreathing cruise and acceleration vehicles at the other end, with all possible shades in between. This is done in order to bring out the different degrees of importance of the aerothermo – dynamic phenomena for them. For the aerothermodynamics of the second vehicle class the fact that the outer surfaces are radiation cooled, is espe­cially taken into account. Radiation cooling governs the thermal state of the surface, and hence all thermal surface effects. At the center of attention is

the flight in the Earth atmosphere at speeds below approximately 8 km/s and at altitudes below approximately 100 km.

The second development is taken into account only indirectly. The reader will not find much in the book about the basics of discrete numerical methods. Emphasis was laid on the discussion of flow physics and thermo-chemical phe­nomena, and on the provision of simple methods for the approximate quan­tification of the phenomena of interest and for plausibility checks of data obtained with numerical methods or with ground-simulation facilities. To this belongs also the introduction of the Rankine-Hugoniot-Prandtl-Meyer – (RHPM-) flyer as highly simplified configuration for illustration and demon­stration purposes.

The author believes that the use of the methods of numerical aerother – modynamics permits much deeper insights into the phenomena than was possible before. This then warrants a good overall knowledge but also an eye for details. Hence, in this book results of numerical simulations are discussed in much detail, and two major case studies are presented. All this is done in view also of the multidisciplinary implications of aerothermodynamics.

The basis of the book are courses on selected aerothermodynamic design problems, which the author gave for many years at the University of Stuttgart, Germany, and of course, the many years of scientific and industrial work of the author on aerothermodynamics and hypersonic flight vehicle design problems. The book is intended to give an introduction to the basics of aerothermodynam – ics for graduate students, doctoral students, design and development engineers, and technical managers. The only prerequisite is the knowledge of the basics of fluid mechanics, aerodynamics, and thermodynamics.

The first two chapters of introductory character contain the broad vehicle classification mentioned above and the discussion of the flight environment. They are followed by an introduction to the problems of the thermal state of the surface, especially to surface radiation cooling. These are themes, which reappear in almost all of the remaining chapters. After a review of the issues of transport of momentum, energy and mass, real-gas effects as well as inviscid and viscous flow phenomena are treated. In view of the importance for air­breathing hypersonic flight vehicles, and for the discrete numerical methods of aerothermodynamics, much room is given to the topic of laminar-turbulent transition and turbulence. Then follows a discussion of strong-interaction phe­nomena. Finally a overview over simulation means is given, and also some supplementary chapters.

Throughout the book the units of the SI system are used, with conversions given at the end of the book. At the end of most of the chapters, problems are provided, which should permit to deepen the understanding of the material and to get a ”feeling for the numbers”.

Zorneding, April 2004

The author is much indebted to several persons, who read the book or parts of it, and gave critical and constructive comments.

First of all I would like to thank G. Simeonides and W. Kordulla. They read all of the book and their input was very important and highly appreci­ated.

Many thanks are due also to A. Celic, F. Deister, R. Friedrich, S. Hein, M. Kloker, H. Kuczera, Ch. Mundt, M. Pfitzner, C. Weiland, and W. Staudacher, who read parts of the book.

Illustrative material was directly made available for the book by many colleagues, several of them former doctoral and diploma students of mine. I wish to thank D. Arnal, J. Ballmann, R. Behr, G. Brenner, S. Briick, G. Dietz, M. Fertig, J. Fischer, H.-U. Georg, K. Hannemann, S. Hein, A. Henze, R. K. Hold, M. Kloker, E. Kufner, J. M. Longo, H. Lidecke, M. Marini, M. Mharchi, F. Monnoyer, Ch. Mundt, H. Norstrud, I. Oye, S. Riedelbauch, W. Schroder, B. Thorwald, C. Weiland, W. Zeiss. General permissions are acknowledged at the end of the book.

Special thanks for the preparation of the figures is due to H. Reger, S. Klingenfuss, B. Thorwald, and F. Deister, and to S. Wagner, head of the Institut fur Aerodynamic und Gasdynamik of the University of Stuttgart, for sponsoring much of the preparation work.

Finally I wish to thank my wife for her support and her never exhausted patience.

Ernst Heinrich Hirschel

In this book basics of aerothermodynamics are treated, which are of importance for the aerodynamic and structure layout of hypersonic flight vehicles. It appears to be useful to identify from the beginning classes of hy­personic vehicles, because aerothermodynamic phenomena can have different importance for different vehicle classes. This holds in particular for what is usually called “viscous effects”. In view of them we introduce in this book the “thermal state of the surface”, which—besides the classical similarity parameters—governs “thermal surface effects” on wall and near-wall viscous – flow and thermo-chemical phenomena, as well as “thermal (heat) loads” on the structure.

1.1 Classes of Hypersonic Vehicles and Their Aerothermodynamic Peculiarities

The scientific and technical discipline “aerothermodynamics” is multidisci­plinary insofar as aerodynamics and thermodynamics are combined in it. However, recent technology work for future advanced space transportation systems has taught that “aerothermodynamics” should be seen from the be­ginning in an even larger context.

In aircraft design, a century old design paradigm exists, which we call Cayley’s design paradigm, after Sir George Cayley (1773-1857), one of the early English aviation pioneers [1]. This paradigm still governs thinking, pro­cesses and tools in aircraft design, but also in spacecraft design. It says that one ought to assign functions like lift, propulsion, trim, pitch and yaw stabi­lization and control, etc., plainly to corresponding subsystems, like the wing, the engine (the propulsion system), the tail unit, etc. These subsystems and their functions should be coupled only weakly and linearly. Then one is able to treat and optimize each subsystem with its function, more or less indepen­dent of the others, and nevertheless treats and optimizes the whole aircraft which integrates all subsystems.

For space planes, either re-entry systems, or cruise/acceleration systems (see the classification below), Cayley’s paradigm holds only partly. So far this was more or less ignored. But if future space-transportation systems are

(C Springer International Publishing Switzerland 2015 E. H. Hirschel, Basics of Aerothermodynamics,

DOI: 10.1007/978-3-319-14373-6 _1
to be one order of magnitude more cost-effective than now, and airbreathing hypersonic aircraft are to become reality, it must give way to a new paradigm. This should be possible because of the rise of computer power, provided that proper multidisciplinary simulation and optimization methods can be developed and brought into practical use [2].

It is not intended to introduce such a new paradigm in this book. However, it is tried to present and discuss aerothermodynamics in view of the major roles of it in hypersonic vehicle design, which reflects the need for such a new paradigm.

Different hypersonic vehicles pose different aerothermodynamic design problems. In order to ease the discussion, four major classes of hypersonic vehicles are introduced.[1] These are, with the exception of class 4, classes of winged vehicles which fly with aerodynamic lift in the Earth atmosphere at altitudes below approximately 100 km, and with speeds below 8 km/s, Fig. 1.1.[2]

Fig. 1.1. The four major classes of hypersonic vehicles and some characteristic aerothermodynamic phenomena [4].

Of the below mentioned vehicles so far only the Space Shuttle Orbiter (the Russian BURAN flew only once) actually became—and was—operational. All other are hypothetical vehicles or systems, which have been studied and/or developed to different degrees of completion, see, e. g., [5]—[7]. The four classes are:

1. Winged re-entry vehicles (RV’s), like the US Space Shuttle Orbiter and the X-38,[3] the Russian BURAN, the European HERMES, the Japanese HOPE. RV’s are launched typically by means of rocket boosters, but can also be the rocket propelled upper stages of two-stage-to-orbit (TSTO) space-transportation systems like SANGER, STAR-H, RADI­ANCE, MAKS.

2. Cruise and acceleration vehicles with airbreathing propulsion (CAV’s), like the lower stages of TSTO systems, e. g., SANGER, STAR-H, RA­DIANCE, but also hypothetical hypersonic air transportation vehicles (Orient Express, or the SANGER lower stage derivative). Flight Mach numbers would lie in the ram propulsion regime up to M= 7, and in the scram propulsion regime up to M= 12 (to 14).[4]

3. Ascent and re-entry vehicles (ARV’s)—in principle single-stage-to-orbit (SSTO) space-transportation systems—with airbreathing (and rocket) propulsion like the US National Aerospace Plane (NASP/X30), Ori – flamme, HOTOL, and the Japanese Space Plane. The upper stages of TSTO-systems and purely rocket propelled vehicles, like Venture Star/X33, FESTIP FSSC-01, FSSC-15 etc. are not considered to be ARV’s, because with their large thrust at take-off they do not need low – drag airframes.

4. Aeroassisted orbital transfer vehicles (AOTV’s), also called Aeroassisted Space Transfer Vehicles (ASTV’s), see, e. g., [12].

Each of the four classes has specific aerothermodynamic features and mul­tidisciplinary design challenges. These are summarized in Table 1.1.[5]

Without a quantification of features and effects we can already say, see also Fig.1.1, that for CAV’s and ARV’s (in their airbreathing propulsion mode) viscosity effects, notably laminar-turbulent transition and turbulence (which occur predominantly at altitudes below approximately 40 km to 60 km) play

a major role, whereas thermo-chemical effects are very important with RV’s, ARV’s (in their re-entry mode), and AOTV’s. With the latter, in particu­lar plasma effects in the bow-shock layer (ionization, radiation emission and absorption) have to be taken into account [12].

In Table 1.1 aerothermodynamic and multidisciplinary design features of the four vehicle classes are listed. The main objective of this list is to sharpen the perception, that for instance a CAV, i. e., an airbreathing flight system, definitely poses an aerothermodynamic (and multidisciplinary) design prob­lem quite different from that of a RV. The CAV is aircraft-like, slender, flies at small angles of attack, all in contrast to the RV. The RV is a pure re-entry vehicle, which is more or less “only” a deceleration system, however not a ballistic one. Therefore it has a blunt shape, and flies at large angles of attack in order to increase the effective bluntness.[6]

Thermal loads always must be considered together with the structure and materials concept of the respective vehicle, and its passive or active cooling concept. As will be discussed later, the major passive cooling means for outer surfaces is surface-(thermal-)radiation cooling [14]. The thermal management of a CAV or ARV must take into account all thermal loads (heat sources), cooling needs and cooling potentials of airframe, propulsion system, sub­systems, and cryogenic fuel system.