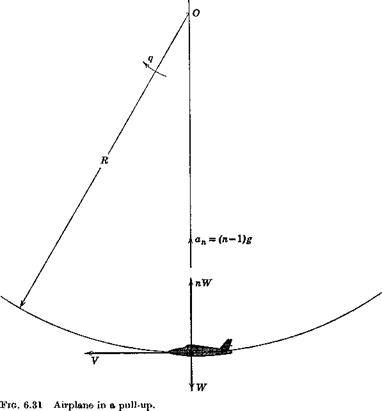
In this section we investigate the elevator angle and control force required to hold a vehicle in a steady pull-up with load factorf n (Fig. 6.31). The concepts discussed here were introduced by S. B. Gates, ref. 6.12. The flight – path tangent is horizontal at the point under analysis, and hence the net normal force is L— W = (n— l)W vertically upward. The normal acceleration is therefore (n — l)g.
When the vehicle is in straight horizontal flight at the same speed and altitude, the elevator angle and control force to trim are Se and P, respectively. When in the pull-up, these are changed to de + ASe and P + ДP. The ratios Adj{n — 1) and AP/(n — 1) are known, respectively, as the elevator angle per g, and the control force per g. These two quantities provide a measure of the maneuverability of the vehicle; the smaller they are, the more maneuverable it is.
The angular velocity of the airplane is fixed by the speed and normal acceleration (Fig. 6.31).
q = ІП – i)g (6.10,1)
As a consequence of this angular velocity, the field of the relative air flow past the airplane is curved. It is as though the machine were attached to the end of a whirling arm pivoted at 0. This curvature of the flow field alters the pressure distribution and the aerodynamic forces from their values in translational flight. The change is large enough that it must be taken into account in the equations describing the motion.
j The load factor is the ratio of lift to weight, n — LjW. It is unity in straight horizontal flight.
We assume that q and the increments Да, ASe etc. between the rectilinear and curved flight conditions are small, so that the increments in lift and moment may he written
ACL = CLx Да + CfJ + CLi A6e (6.10,2)
= СШа Да + Стя4 + Gms A6e (6.10,3)
where q = qc/2V, CL^ — dGLjdq, Cm^ = dCm/d4 (see Sec. 5.13). The q derivatives are discussed in Sec. 7.9. In this form, these equations apply to any configuration. From (6.10,1) we get
which is more conveniently expressed in terms of Gw and ц (see Table 5.1),
4 = (n – 1) (6.10,4)
2fl
Since the curved flight condition is also assumed to be steady, i. e. without angular acceleration, then ДGm = 0. Finally, we can relate AGL to n thus:
= nrr = (» – 1 )0W (6.10,5)
Equations (6.10,2 and 3) therefore become
(n – 1)Cw = CLx Да + (n – 1)CLa °-S. + Gu Ade
‘ 0 = Gmx Да + (» – 1 )Cm^ + Cm3 Ade
which are readily solved for Да and Д6e to yield the elevator angle per g
where Д is given by (6.4,13). As has been shown in Sec. 6.4 Д does not depend on C. G. position, hence the variation of Дdj(n — 1) with h is provided by the terms in the numerator. Writing (7 = 0LJh — hn) (6.10,6a) becomes
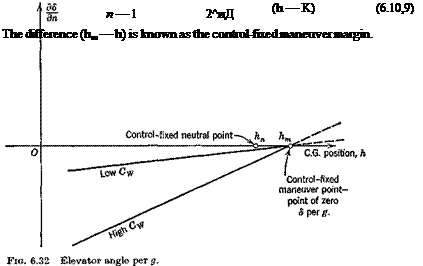
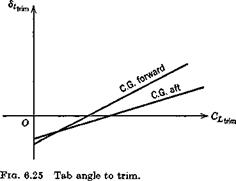
The derivatives CL and Gm both in general vary with h, the former linearly, the latter quadratically, (see Sec. 7.9). Thus (6.10,7), although it appears to be linear in h, is not exactly so. For airplanes with tails, 0L can usually be neglected altogether when compared with 2(i, and the variation of Gm^ with h is slight. The equation is then very nearly linear with h, as illustrated in Fig. 6.32. For tailless airplanes, the variation may show more curvature. The point where AdJ(n — 1) is zero is called the control-fixed maneuver point, and is denoted by hm, as shown. From (6.10,7) we see that
where Gm (hm) and CL (hm) are the values of these two derivatives evaluated for h hm. When Gm and CL^ can be assumed to be independent of h, (6.10,7) reduces to
CONTROL FORCE PER g
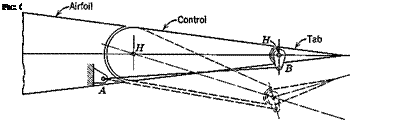
From (6.8,4) we get the incremental control force
AP = QSMpr* AGhe (6.10,10)
Ghe is given for rectilinear flight by (6.5,2). Since it too will in general be influenced by q, we write for the incremental value (Ad( = 0)
AGhe = СЫх Да + GKq + Ьг Аде (6.10,11)
The derivative Ch is discussed in Sec. 7.9. Using (6.10,4) and (6.10,66), (6.10,11) is readily expanded to give
From (6.6,4) we note that the last parenthetical factor is b2G’LJGL^ or Ъга’ ja. For Ade we use the approximation (6.10,9) in the interest of simplicity and the result for AGhe after some algebraic reduction is
= ~ Sr ~ h’m) (6.10,13)
n — 1 2(1 A
where h’m = K + 4г(тг + ) (6-10,14)
a b2CLx 2ц – CLJ
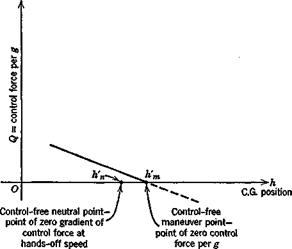
In keeping with earlier nomenclature, h’m is the control-free maneuver point and (h’m — h) is the corresponding margin. On noting that GwpVz is the wing loading w, we find the control force per g is given by
Q = ——г = ^ (2(t – CL )(h – h’n) (6.10,15)
n — 1 2(iA я
Note that this result applies to both tailed and tailless aircraft provided that the appropriate derivatives are used. The following conclusions may be drawn from (6.10,15).
1. The control force per g increases linearly from zero as the C. G. is moved forward from the control-free maneuver point, and reverses sign for h > h’m.
2. It is directly proportional to the wing loading. High wing loading produces “heavier” controls.
3. For similar aircraft of different size but equal wing loading, Q oc Sece;
i. e. to the cube of the linear size.
4. Neither 0L nor V enters the expression for Q explicitly. Thus, apart from M and Reynolds number effects, Q is independent of speed.
5. The factor fi which appears in (6.10,14) causes the separation of the control-free neutral and maneuver points to vary with altitude, size, and wing loading, in the same manner as the interval (hm — hn).
Figure 6.33 shows a typical variation of Q with C. G. position. The statement made above that the control force per g is “reversed” when h > h’m must be interpreted correctly. In the first place this does not necessarily mean a reversal of control movement per g, for this is governed by the elevator angle per g. If h’m < h < hm, then there would be reversal of Q without reversal of control movement. In the second place, the analysis given applies only to the steady state at load factor n, and throws no light whatsoever on the transition between unaccelerated flight and the pull-up condition. No matter what the value of h, the initial control force and movement required to start the maneuver will be in the normal direction (backward for a pull – up), although one or both of them may have to be reversed before the final steady state is reached.
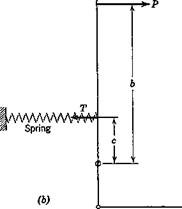 Control column-
Control column-![]()
![]() ДР = nW – Ъ
ДР = nW – Ъ![]() ДР — Tb
ДР — Tb












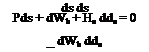
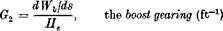 and
and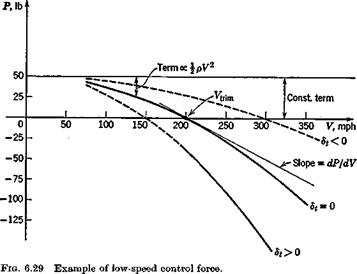

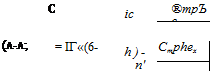
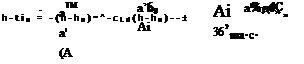
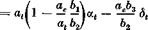 (6.6,8)
(6.6,8)