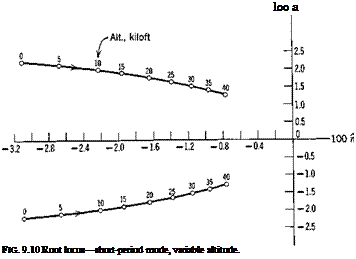
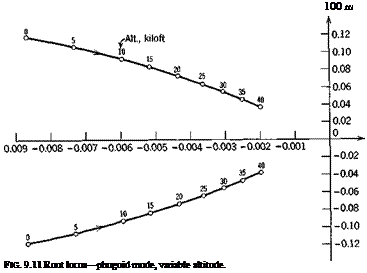
The effect of the vertical gradient in atmospheric density on the characteristic modes of horizontal flight was first discussed by Scheubel (ref. 9.1), and later in more detail by Neumark (ref. 9.2) and Walkowicz (ref. 9.3). Their principal conclusions were that the short-period motion is unchanged by the density gradient, but that the phugoid period is appreciably shortened by an amount that increases with speed. Neumark also pointed out that the characteristic equation for this case is of the fifth degree and that the extra root is a small one corresponding to the tendency of the vehicle to seek or depart from its equilibrium altitude, depending on whether or not the root is negative. Neumark concluded, based on examples in which the thrust was independent of height, that the damping of the phugoid was unaffected by dp/dz. In fact, the phugoid damping is very sensitive to the thrust law, and as shown in the example that follows, in which Toe pso that C’2,_ = 0 (a reasonable approximation for jet engines), the damping can be very much reduced at all speeds by the density gradient. Before proceeding to the numerical solutions of the complete equations however, it is instructive to present Scheubel’s extension of the simple Lanchester analysis of the phugoid period. In Sec. 9.2 we saw that with Lanchester’s approximations there is a vertical “spring stiffness” к given by (9.2,3) that governs the period. When the density varies there is a second “stiffness” k’ resulting from the fact that the increased density when the vehicle is below its reference altitude increases the lift, and vice versa. This incremental lift associated with a density change is
Д£ = Cl§V2S Др
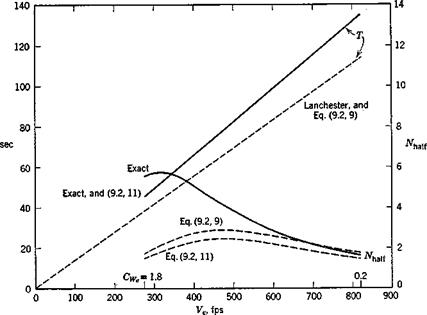
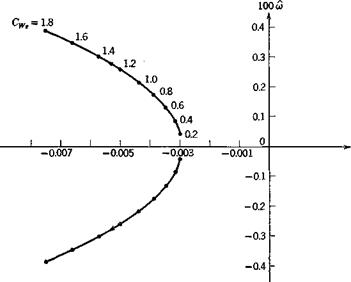
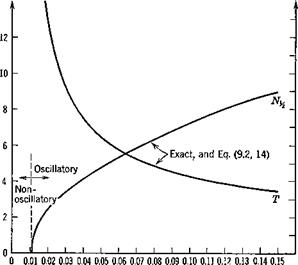
in which the principal variable is seen to be the speed, occurring in the form of the Froude’s number (V*jgc)- The reduction in phugoid period predicted by (9.4,7) for the example airplane is 14% at 500 mph, which is very close to the exact result of 13% (Fig. 9.14).
In order to provide a complete comparison with the approximation based on constant density, we use the fifth-order system (5.13,18) to make numerical calculation for the same conditions as hold in Figs. 9.4 and 9.5. All the z derivatives CT, Cn_, CL, Cmz have been assumed to he zero, and the only density-gradient effects are embodied in the dpjdz terms. Note that CTz = 0 implies a propulsion system in which the thrust is proportional to p. With all the assumptions that pertain to this example explicitly incorporated, the system matrix is
|
Ve, fps
Fig. 9.14 Effect of density gradient on phugoid characteristics. Altitude 30,000 ft.
|
The value of dp/dz was obtained from the tables for the U. S. Standard Atmosphere (ref. 9.14) as follows:
dp _ 1 c dp _ c d log p (g 4 9)
dz pe2 dz 2 dh
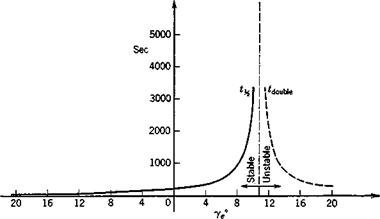
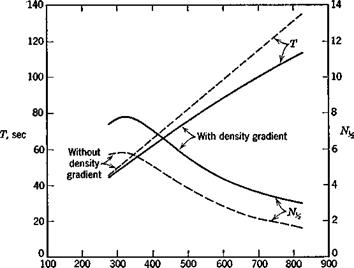
where h is the altitude. From the tabulated data, d log pjdh at about 30,000 ft altitude is found to be —4.16 X 10~5 and hence dp/dz = f(15.40)(4.16)10~5 = .000320. With this value, the eigenvalues of (9.4,8) have been calculated for the same range of speeds as used in Figs. 9.4 and 9.5. The short-period mode is found to he unchanged to three significant digits, in agreement with Neumark, the phugoid damping and period are both altered, and a new stable nonoscillatory mode of long time constant appears. Figure 9.14 shows the quite substantial effects on the phugoid. It is clear from these graphs that neglect of atmospheric density gradient can lead to considerable error. This is especially significant with respect to the damping since the constant-density approximation gives unconservative results.
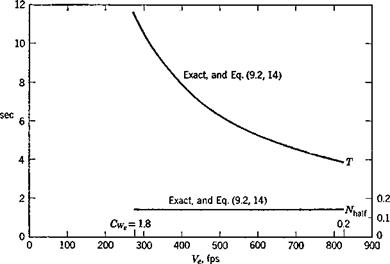
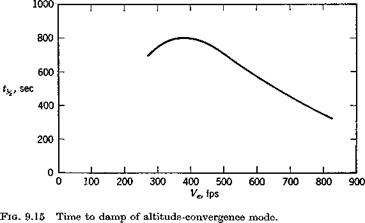
The fifth root of the characteristic equation is negative, corresponding to a stable subsidence. Its characteristic time, plotted on Fig. 9.15, is seen to be very long. This mode is related to the weak tendency of the vehicle to fly at its equilibrium altitude (note that there is no preferred altitude in the constant-density case). The eigenvector of this mode for Ve = 561 mph
is found to Ъе Д1^:Да:$:&6:zB = —.161 x 10~s:.187 x 10—7: — .398 x 10~9: .199 x 10_4:1 which shows that, like the phugoid, it is a mode with negligible Да and q. That is, it is an “arrow” mode, in which the vehicle axis is closely aligned with the velocity vector while it drifts slowly back to its equilibrium altitude. The principal degree of freedom is clearly zE. The relative magnitudes are a little deceptive however because of the small length (c/2) used to make zE nondimensional. For this vehicle, a decrease in altitude of 1000 ft in this mode would correspond to ДzE = 130 and a Д7 of —2%.
It is instructive to examine the approximation obtained by neglecting Да and the Gm equation, just as was done previously with the fourth-order system. For additional generality, to allow for other than jet engines, we retain the term СТг in the first equation. When the same procedure is followed as led to (9.2,9) the result is the cubic characteristic equation
When the thrust is independent of height and speed, as for a rocket engine, GTi is given by (7.12,1) as GTs = —GTe dp/dz and GTy = ~2GT^. The last term of (9.4,10) then disappears, one root is zero, and the remaining two are given by
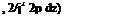 Gm
Gm
2/jl
Without the dp/dz term, this is exactly the phugoid approximation (9.2,9),
and the constant term can be identified exactly as the augmented “spring – constant” that led to (9.4,7)—note that the ratio of the last two terms is
G^dp = Vld_l
2pi dz ‘ 2p? gc d
It is clear that the approximation to the fifth root in this case is A = 0, and that the phugoid is changed only to the extent of the reduced period. The damping term CTyj2pt is unaffected by the presence of the density gradient. This is consistent with Neumark’s finding for examples in which T is constant.
When the propulsion system is comprised of jet engines, a reasonable approximation is T oc p and independent of V, in which case GTy = 2GT = —2CD’ and СТг — 0. The last term of (9.4,10) is then (GDGwJ2pi)(dpjdz), a small positive constant. An approximation to the fifth root is obtained by neglecting the s2 and. s3 terms of (9.4,10) with the result
This actually gives a very good approximation to this root for the example treated. It is seen to correspond to a stable convergence. The effect on the remaining phugoid roots can now be inferred. The coefficient of the next-to – the-highest order term in any characteristic equation is equal to the negative of the sum of the roots. f Since the imaginary parts cancel the result is the “sum of the dampings.” In this case this yields
GT CD
2 nm + *5=+-^=-—*
2 pi pi
where the phugoid roots are nph ± It follows that the “sum of the dampings” is a constant, and hence that the presence of the stable fifth root must be accompanied by a reduction in the damping of the phugoid. Specifically
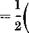
 £d.
£d.
For the example case at Cw = .20, this gives the reduction in phugoid damping from the constant-density case, Awithin about 1 %.
In summary, it is clear that even at subsonic speeds the classical “stability quartic” derived from a uniform-atmosphere model can be significantly in
f Verify by comparing l. h.s. and r. h.s. of (s — /j) (.v — /•>) • • • (s — in) — sn + cn_-^sn 1 + • • • c0. — c„-i is equal to the trace of the system matrix A, i. e. to the sum of its diagonal elements.
error with respect to the phugoid roots, and the’ design of autopilot systems to maintain speed and/or altitude may require the use of the more accurate model. At supersonic speeds the effect of density gradient is larger still. However it should be noted that the flat-Earth model itself becomes inadequate at high supersonic speeds (see Sec. 9.10).
![]() The aerodynamic transfer functions on the r. h.s well enough by (see Sec. 5.14)
The aerodynamic transfer functions on the r. h.s well enough by (see Sec. 5.14)![]() G/iia ‘ ■ Gma “I – sGm^
G/iia ‘ ■ Gma “I – sGm^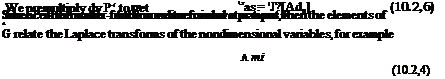











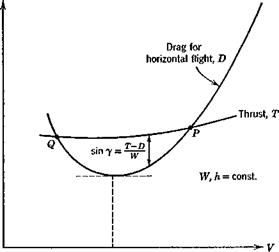
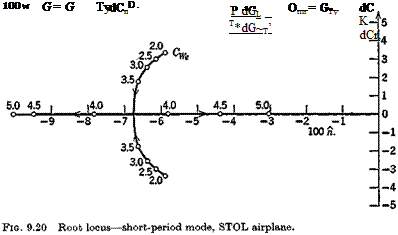
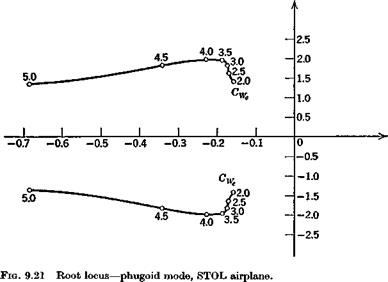
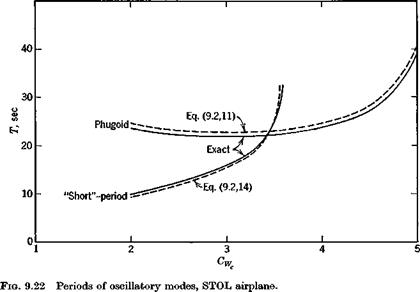
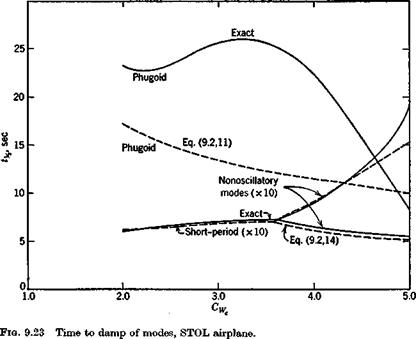
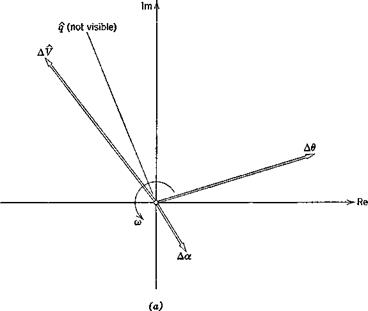
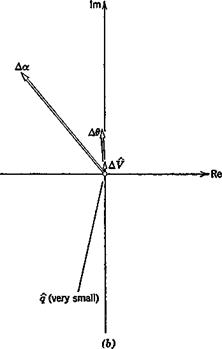
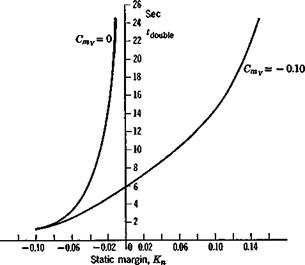
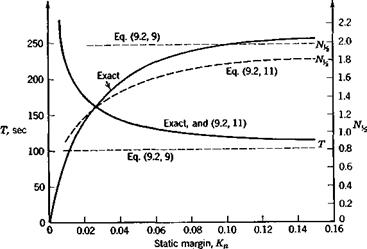
 0.24
0.24
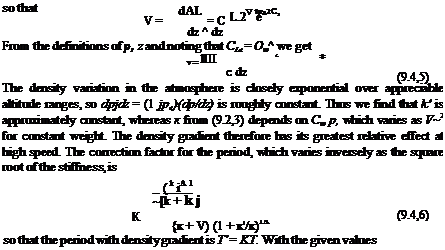

 34
34