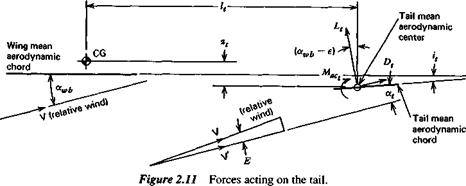
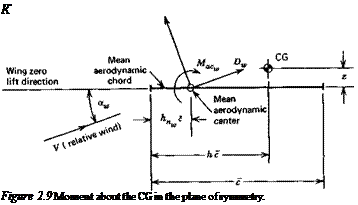
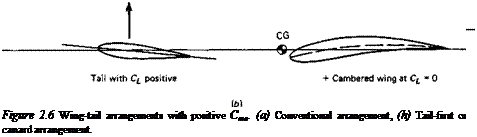
PITCHING MOMENT OF A PROPULSIVE SYSTEM
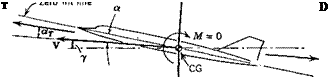
The moment provided by a propulsive system is in two parts: (1) that coming from the forces acting on the unit itself, for example, the thrust and in-plane force acting on a propeller, and (2) that coming from the interaction of the propulsive slipstream with the other parts of the airplane. These are discussed in more detail in Sec. 3.4. We assume that the interference part is included in the moments already given for the wing, body, and tail, and denote by Cmp the remaining moment from the propulsion units.
2.2 Total Pitching Moment and Neutral Point
On summing the first of (2.2,4) and (2.2,13) making use of (2.2,6) and adding the contribution Cmp for the propulsive system, we obtain the total pitching moment about the CG
Cm = Gmo<,B, k + CL(h – hnJ – VHCL, + (2.3,1)
It is worthwhile repeating that no assumptions about thrust, compressibility, or aero – elastic effects have been made in respect of (2.3,1). The pitch stiffness ( —CmJ is now obtained from (2.3,1). Recall that the mean aerodynamic centers of the wing-body combination and of the tail are fixed points, so that
If a true mean aerodynamic center in the classical sense exists, then dCmacJda is zero and
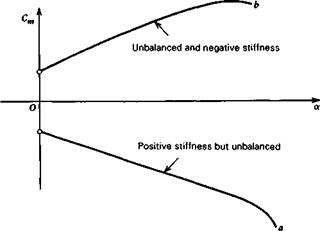
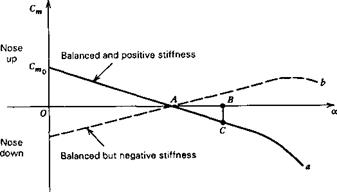
Cma as given by (2.3,2) or (2.3,3) depends linearly on the CG position, h. Since CI y is usually large, the magnitude and sign of Cma depend strongly on h. This is the basis of the statement in Sec. 2.2 that Cma can always be made negative by a suitable choice of h. The CG position hn for which Cma is zero is of particular significance, since this represents a boundary between positive and negative pitch stiffness. In this book we define hn as the neutral point, NP. It has the same significance for the vehicle as a whole as does the mean aerodynamic center for a wing alone, and indeed the term vehicle aerodynamic center is an acceptable alternative to “neutral point.”
The location of the NP is readily calculated from (2.3,2) by setting the left-hand side to zero leading to
Substitution of (2.3,4) back into (2.3,2) simplifies the latter to
Cm„ = CLa(h ~ hn) (2.3,5)
which is valid whether and Cm vary with a or not. Equation (2.3,5) clearly
provides an excellent way of finding hn from test results, that is from measurements of Cma and CL y. The difference between the CG position and the NP is sometimes called the static margin,
Kn = (hn – h) (2.3,6)
Since the criterion to be satisfied is Cnia < 0, that is, positive pitch stiffness, then we see that we must have h < hn, or Kn > 0. In other words the CG must be forward of the NP. The farther forward the CG the greater is Kn, and in the sense of “static stability” the more stable the vehicle.
The neutral point has sometimes been defined as the CG location at which the derivative dCJdCL = 0. When this definition is applied to the gliding flight of a rigid
airplane at low Mach number, the neutral point obtained is identical with that defined in this book. This is so because under these restricted conditions C, is a unique function of a, and dCJdCL = (dCJda)/(dCL/da). Then dCJdCL and dCJda are simultaneously zero. In general, however, Cm and CL are both functions of several variables, as pointed out at the beginning of Sec. 2.2. For fixed values of Se and h, and neglecting Reynolds number effects (these are usually very small), we may write
CL = f(a, M, C-n hPV2), Cm = g(a, M, CT, pV2) (2.3,7)
where CT is the thrust coefficient, defined in Sec. 3.15.
Mathematically speaking, the derivative dCJdCL does not exist unless M, C7, and pV2 are functions of C,. When that is the case, then
dCm _ 3C,„ da ЭCm ЭМ dCm dCT dCm d(hpV2) ^ ^
dCL da dCL ЭМ dCL + dCT dCL + d{pV2) dCL (2’3’8)
Equation 2.3,8 has meaning only when a specific kind of flight is prescribed: e. g.,
horizontal unaccelerated flight, or rectilinear climbing flight at full throttle. When a condition of this kind is imposed, then M, CT, and the dynamic pressure are definite functions of CL, dCJdCL exists, and a neutral point may be calculated. The neutral point so found is not an index of stability with respect to angle of attack disturbances, and the question arises as to what it does relate to. It can be shown that it relates to the trim curves of the airplane. A plot of the elevator angle to trim versus speed will have a zero slope when dCJdCL is zero, and a negative slope when the CG lies aft of the neutral point so defined. As shown in Sec. 2.4, this reversal of slope indicates a tendency toward instability with respect to speed, but only a dynamic analysis can show whether or not the airplane is stable in this condition. There are cases when the application of the “trim-slope” criterion can be definitely misleading as to stability. One such is level unaccelerated flight, during which the throttle must be adjusted every time the flight speed or CL is altered.
It can be seen from the foregoing remarks that the “trim-slope” criterion for the neutral point does not lead to any definite and clear-cut conclusions, either about the stability with respect to angle of attack disturbances, or about the general static stability involving both speed and angle of attack disturbances. It is mainly for this reason that the neutral point has been defined herein on the basis of dCJda.