Category FLIGHT MECHANICS MODELING and ANALYSIS

The subject of flight mechanics has been studied for nearly 100 years, in one or more ways. There have been many advances in the theory and approaches to understand­ing various aspects of flight mechanics, and several researchers and engineers all over the world have made contributions to this specialized field, which has emerged as an independent discipline from basic aerodynamics and applied mechanics.

We are very grateful to S. Balakrishna and S. Srinathkumar who initiated research and project activities in flight mechanics and control in NAL several decades ago. Balakrishna built the first 3DOF motion-based simulator in 1976 at the National Aerospace Laboratories (NAL) for investigating human operator modeling. The major impetus to the activity came from the country’s indigenous fighter aircraft and missile development programs, which supported the sponsored activities in the areas of modeling and identification, flight simulation, and flight control. Srinathkumar led the control-law team for a decade on the fighter aircraft development program.

We are grateful to several aeronautical and flight testing agencies in India and a few overseas (via a cooperative exchange program), which have, in some ways, supported the research and development in these areas at NAL. We are really grateful to all the past and present directors of NAL who vehemently supported in-house research activities for all these years. Thanks are also due to Professor N. K. Sinha (professor emeritus, McMaster University, Canada) and Professor R. C. Desai (M. S. University of Baroda, Vadadora, India) for their moral support.

We appreciate the constant technical support of several colleagues from flight mechanics and control disciplines, who have tirelessly and very ably furthered the cause of flight mechanics and control research and applications from NAL’s plat­form: Padma Madhuranath, Shyam Chetty, Girija Gopalratnam, R. V. Jategaonkar, Girish Deodhare, V. Parameswaran, Abhay Pashilkar, M. S. Rajamurthy, Shaik Ismail, A. Santharam, N. Shanthakumar, G. K. Singh, Amitabh Saraf, Vijay Patel, Ambalal Patel, Yogananda, P. Lathasree, Basappa, Saraswathi, Moncy Thomas, P. V.S. Murthy, K. P. Srikanth, V. S. Mohan Ram, P. Laksmi, Srikantha Rao, Sura, Vineetkumar, and B. Chakravarthy, and many others not mentioned here for the sake of brevity. We are also grateful to Professors Hamel, Doherr, Plaetschke, Levadag, Thielecke, and many other scientists of the DLR Institute of Flight Systems, who have constantly encouraged us over the years. We are also very grateful to Sudesh Kashyap and Mangal Kothari for their help with MATLAB® progams. We are grateful to Jonathan Plant, editor at CRC Press, for his continual support during this project. We are, as ever, very grateful to our spouses and children for their understanding, endurance, care, and affection.

xvn

Jitendra R. Raol received his BE and ME in electrical engineering from M. S. University of Baroda, Vadodara, in 1971 and 1973, respectively, and a PhD (in electrical and computer engineering) from McMaster University, Hamilton, Canada, in 1986. He taught for 2 years at the M. S. University of Baroda before joining the National Aeronautical Laboratory (NAL) in 1975. At NAL he was involved in activities on human pilot modeling in fix – and motion-based research simulators. He rejoined NAL in 1986 and retired on July 31, 2007, as scientist-G (and head, flight mechanics and control division at NAL). He has visited Syria, Germany, the United Kingdom, Canada, China, the United States, and South Africa on deputation/fellowships to work on research problems on parameter estimation and multisensor data fusion and to present papers at several international conferences. He became fellow of the IEE (United Kingdom) and a senior member of the IEEE (United States). He is a life fellow of the Aeronautical Society of India and a life member of the Systems Society of India. In 1976, he won the K. F. Antia Memorial Prize of the Institution of Engineers (India) for his research paper on nonlinear filtering. He was awarded a certificate of merit by the Institution of Engineers (India) for his paper on parameter estimation for unstable systems. He received the best poster paper award from Center for Environment and Explosive Safety (DRDO) for his paper on tracking and trajectory estimation. He is one of the recipients of the CSIR technology shield for the year 2003 for contributions to integrated flight mechanics and control technology for aerospace vehicles.

Dr. Raol has published 85 research papers and several reports. He was a guest editor for special issues of Sadhana on advances in modeling, system identification, and parameter estimation and on multisource, multisensor information fusion pub­lished by the Indian Academy of Sciences, Bangalore. He has guided several doctoral/masters students and has coauthored an IEE (United Kingdom) Control Series book Modeling and Parameter Estimation of Dynamic Systems. He has served as a member/chairman of several advisory, technical project review, and doctoral examination committees. His main interests are data fusion, parameter estimation, flight mechanics-flight data analysis, filtering, artificial neural networks, fuzzy systems, and genetic algorithms.

Jatinder Singh has been a senior scientist at the flight mechanics and control division of National Aerospace Laboratories, Bangalore, since 1998. He has a PhD in aerospace engineering from IIT, Kanpur. He is a recipient of the Alexander von Humboldt fellowship and has worked as a guest scientist at the DLR Institute for Flight Systems, Braunschweig, Germany. Dr. Singh is a senior member of the AIAA and a life member of the Aeronautical Society of India and Systems Society of India. He is recipient of the NAL Foundation Day Award and was a member of the team that won the CSIR technology shield for the year 2003, awarded to the flight mechanics and control division of NAL for contributions to integrated flight mechanics and control technology for aerospace vehicles. He has been extensively involved in aircraft modeling and parameter estimation work and has several conference and journal papers to his credit. He also coauthored Modelling and Parameter Estimation of Dynamic Systems, published by IEE, London, in 2004.

Flight mechanics is a difficult subject to understand, especially for nonaerospace scientists and engineers. Even aerospace scientists and engineers with a background in pure aerodynamics, propulsion, and structures would find it rather difficult to appreciate various aspects of flight mechanics, especially when applied to flight simulation, flight control, and aircraft parameter estimation. It is strongly felt, with our experience of several decades, that an approach based on systems theory would be useful for a better understanding of flight mechanics, its analysis, and applica­tions. The approach adopted here is via simple concepts of mathematical model building, introduction of flight mechanics, and mathematical representations of its concepts. This leads to the equations of motion (EOM) of an aerospace vehicle and the simplifications to arrive at linear models. Subsequently, the original nonlinear or linear models can be used for further studies and interpretations.

The problems in aircraft dynamics are, often but not always, related to flight simulation, flight control, and system identification. Modeling, identification, para­meter estimation, and simulation play a very significant role in the present-day analysis of complex dynamical systems including aerospace vehicles. The informa­tion obtained from the application of these techniques can be routinely used for flight simulation, design and development of flight-control laws, and prediction (including simulation) of dynamic phenomena of these vehicles. Application of these tech­niques to an aerospace vehicle centers on the knowledge of flight mechanics. The main aim of this book is to strengthen the foundation in flight mechanics using systems theory concepts of mathematical model building, system identification, parameter estimation, and simulation, which provide the defining principles and techniques. Clear understanding of techniques of one field enhances the understand­ing of the other field. Often flight mechanics and flight dynamics are used inter­changeably; however, the study of flight dynamics encompasses flight mechanics analysis. This book emphasizes on flight mechanics and associated studies in model building and their use in various applications that broaden the scope of flight dynamics.

The flight mechanics of an aerospace vehicle can be approached from the fundamental aspects of study of a dynamic system. The dynamics of an aircraft flight are described by aircraft EOM [1-3]. The forces that act on the aircraft are inertial, gravitational, aerodynamic, and propulsive. Aerodynamic forces make a major contribution to flight dynamics. The modeling of aircraft dynamics involves mainly the characterization of aerodynamic forces and moments. Flight motions of an aircraft can be described by nonlinear-coupled differential equations based on Newton’s laws of motion of a rigid body, with several associated constants and parameters, which are mass – and geometry-related coefficients, aerodynamic coefficients, and aerodynamic stability and control derivatives. Simplifications can be carried out using relevant assumptions.

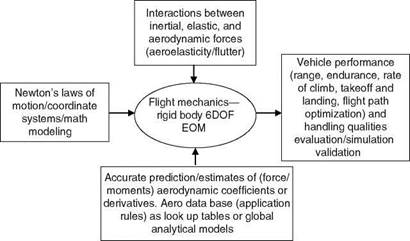
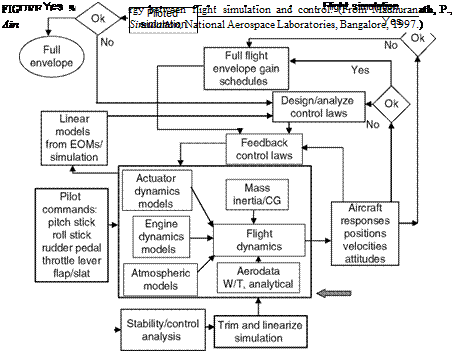
An aircraft can be considered as a dynamic system. A system can be studied directly by conducting some experiments with it or by using its mathematical model. In the case of aircraft both are possible: the former is done when the vehicle is ready for flight tests and the latter is done in the design and development stage. Flight mechanics analysis, flight simulation, and partly the handling quality analysis (HQA) are carried out using mathematical models. Subsequently, flight data are obtained from flight tests on the aircraft under several flight conditions (defined by altitude and Mach number). These data are preprocessed and analyzed by system identification/parameter-estimation methods [4] and the mathematical models (their parameters) are updated, if deemed necessary. In addition, HQs are evaluated based on flight data/flight-determined models and assessments. Thus, there is close interaction between these aspects of flight mechanics analysis, modeling, system identification, parameter estimation, and simulation. Figure 1.1 depicts the inter­action of several disciplines that form the input/output to the study of flight mech­anics. A synergy of the development process of flight control and flight simulation of an aircraft is depicted in Figure 1.2 [5]. In fact aircraft stability and control should be studied from the point of view of applied science because it utilizes information, data, and analysis tools from several disciplines: (1) mathematics, (2) control and systems dynamics, (3) aerodynamics and computational fluid dynamics (CFD), (4) wind-tunnel testing, (5) flight testing, (6) aeroelasticity, (7) flying and handling qualities, (8) flight dynamics simulation, and (9) flight control [6]. Thus, the field of aircraft stability and control has evolved as a mature tool in the design, development, and certification of atmospheric vehicles, mainly airplanes.

For system identification and estimation of aerodynamic derivatives from flight data, one needs to conduct appropriate flight tests and acquire the data. For this task certain special maneuvers are performed by a test pilot to excite the modes of the aircraft. Then one uses parameter/state estimation methods. Aerodynamic derivatives (stability and control), which are parameters in the mathematical model of an aircraft, are required for one or more of the following reasons: (1) explaining aerodynamics, stability, and control behavior of the vehicle, thereby describing its static/dynamic behavior and (2) designing flight-control systems and high-fidelity simulators. Three main approaches used in the estimation of these derivatives are (1) analytical methods (like data compendium [DATCOM], CFD), (2) wind-tunnel testing of scaled models of aircraft, and (3) flight testing and subsequent flight data analysis.

The focus here is on the third approach. The subject of flight tests is very vast and hence we will concentrate only on the flight-test techniques/experiments that are necessary to generate dynamic responses of aircraft with the objective of further analyzing these data to extract the aerodynamic derivatives of aircraft. Similar methods with certain special or degenerate experiments are applicable in the case of other atmospheric or space vehicles. For projectiles, aeroballistic test range facilities are often used. Some important principles and techniques of system iden­tification and state/parameter estimation are covered in this book. The applications
of these techniques to kinematics consistency checking and estimation of aerody­namic derivatives from flight data are discussed. The determination of aircraft performance (drag polars) and HQs from flight-test data is also of great importance. Drag polars can be successfully determined from dynamic maneuver data using parameter-estimation methods. Thus, several important concepts and aspects of flight mechanics analysis from the point of view of modeling and simulation are presented. Here, modeling is approached from the system identification and parameter-estimation point of view.

Although flight-control aspects are not fully discussed in this book, certain aspects are highlighted from the systems theory point of view to emphasize the fact that several key topics presented in the book would be useful and be utilized to appreciate certain aspects of flight-control studies. Many modern fighter aircrafts are designed with unstable configurations, which do not possess natural or inherent stability. Some of the merits of such designs are (1) improvement in performance (i. e., increased lift/drag ratio) and (2) improvement in maneuverability. Essentially, the task of stability has been partially transferred to the control task and hence the emphasis on flight control. Flight-control systems in aerospace vehicles are extended applications of the classical control methods and modern control approaches to the problem of design and development of sophisticated control laws, with one or more of the following purposes:

1. Improve the otherwise poor static stability or damping in dynamics in a given axis

2. Provide stability to inherently unstable aircraft/dynamics

3. Improve the HQs of the aircraft and pilot-aircraft interactions/coupling

4. Improve the safety and reliability of the aircraft’s functions, e. g., in the presence of certain kinds of failures

5. Reduce the workload of the pilot in handling complex flight missions and tasks, e. g., autopilot

Recently, there has been an upward surge in applications of artificial neural networks (ANNs) and fuzzy logic/systems (FL/S) to aid flight-control/autopilot systems.

Today the subject of Flight Mechanics: Modeling and Analysis has assumed great importance in the design, development, analysis, and evaluation (via flight tests) of aerospace vehicles, especially in fly-by-wire aircraft development programs. Study of flight mechanics is important since the understanding of flight dynamics of aerospace vehicles presupposes a good understanding of flight mechanics. It is proposed that this study be undertaken via a systems approach without undermining the importance of the related aerodynamics, which provides the basis of flight mechanics modeling and analysis. The point is that the approach via systems concepts and methods provides natural synergy with flight mechanics applications to design and development of flight control laws, flight simulation, aircraft system identification, parameter estimation, and handling qualities evaluation for a piloted vehicle. Interestingly, several such aspects also apply to unmanned (uninhabited) aerial vehicles and micro-air vehicles. Collectively all the above topics are generally studied and researched under the banner of flight mechanics and control.

In Flight Mechanics: Modeling and Analysis we study some of these topics and emphasize the use of flight mechanics knowledge via modeling and analysis. We illustrate several concepts and methods of flight mechanics as applied to system identification, parameter estimation, simulation, and handling qualities evaluations. We use several numerical simulation examples coded in MATLAB® (MATLAB is the trademark of MathWorks Ltd., Natick, Massachusetts, USA). The user should have access to PC-based MATLAB software and other toolboxes: signal processing, control system, system identification, neural networks, and fuzzy logic.

There are several good books on flight mechanics/dynamics but these either do not approach the subject from the systems point of view or the treatment of such aspects as outlined here is somewhat limited or specialized. Understanding of one field enhances the understanding of the other. The systems approach inherently borrows ideas and concepts from applied mathematics, for example, mathematical model building, especially based on empirical methods, control theory, and signal/data analysis methods. Also, concepts from linear algebra and matrix com­putation are widely used. These basic aspects including a fundamental course on aerodynamics are studied at the undergraduate level. Collective study of these concepts and methods with flight mechanics analysis lends itself to a synergy, which can be described in short as flight mechanics modeling and analysis. This book follows the systems theory approach, which will help readers enhance their understanding of the concepts and application of flight mechanics. It brings about the interrelatedness of various related topics of analysis and modeling. The new gener­ation paradigms of artificial neural network and fuzzy logic-based modeling are gradually making inroads into flight dynamics, modeling, and associated areas of parameter estimation, simulation, and control technologies. Hence, these topics are also discussed here, perhaps, for the first time in a book on flight mechanics.

The end users of this book on the integrated technology of flight mechanics will be those involved in aerosystems educational institutions, aerospace research and development laboratories, aerospace industries, flight test agencies, and transporta – tion/automotive industries. Interestingly, others in some industrial and mechanical engineering centers might benefit from certain aspects of this book.

Jitendra R. Raol Jatinder Singh