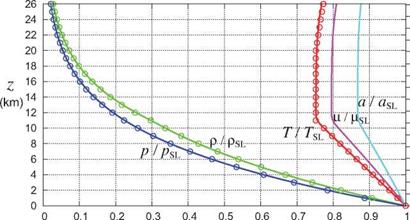
Ideal-Gas Thermodynamic Relations
The ideal gas law
p = pRT (1.7)
R = 287.04 J/kg-K (for air)
is an example of an equation of state, and is accurate for all common gases over a wide range of temperatures and pressures. The specific gas constant R is inversely proportional to the average molecular weight.
An additional important state variable is the specific internal energy e, which together with p and p also defines the specific enthalpy h.
![]() (1.8)
(1.8)
(for ideal gas) (1.9)
For a thermally perfect gas, both e and h depend only on the temperature, and are respectively defined via the specific heat at constant volume cv (T), and the specific heat at constant pressure cp (T).
fT )
e(T) = eref + cv(T’) dT
(thermally perfect gas) (1.10)
h(T) href + °p(T/) dT
Tref
The reference values are arbitrary, since only changes in e and h are physically meaningful. The ideal-gas h definition (1.9) implies the following relation between the specific heats and the specific gas constant.
For a calorically perfect gas, both cv and cp are constant, which makes e and h directly proportional to T,
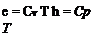 (calorically perfect gas) (1.12)
(calorically perfect gas) (1.12)
where zero reference values have been chosen. Air at ordinary temperatures is very nearly calorically perfect. Hence, definitions (1.12) are appropriate for external aerodynamic flows, and here it is more natural to work directly with the enthalpy rather than the temperature. A more convenient form of the ideal gas law (1.7) is then given in terms of the enthalpy and the specific heat ratio 7.
|
|
|
|||
|
|||||
|
|||||
|
|||||
![]()
In extreme conditions, such as those inside gas turbine hot sections, cv and cp can no longer be assumed to be independent of temperature, so the more general e(T) and h(T) definitions (1.10) must be used. Also, y then depends on temperature and thus has limited applicability. However, R is still nearly constant and the temperature form of the ideal gas law (1.7) still applies.