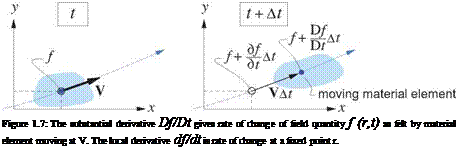
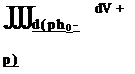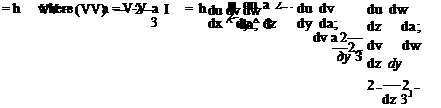High Reynolds number flows
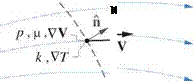
Typical aerodynamic flows of interest have very large Reynolds numbers, or Reref ^ 1, when based on a typical body dimension and freestream velocity and viscosity. Because the viscous-stress and heat conduction terms involving t and q in equations (1.46),(1.47) are scaled by 1/Reref, these terms must therefore be negligible over most of the flow-field. The exception occurs very close to a body surface where V ^ 0 because of the no-slip condition. Here, in the momentum equation (1.46) only Vp remains to balance the viscous term, so the latter must remain significant sufficiently close to a wall. The result is that the action of viscosity and heat conductivity is confined to boundary layers and wakes, collectively termed the “shear layers” or “viscous regions.”
 |
The viscous regions will be examined in much more detail in Chapters 3 and 4. For now, it will suffice to say that at the high Reynolds numbers of typical aerodynamic flows, the viscous regions, distinguished by significant t and q, are very thin compared with the body size, as sketched in Figure 1.9. This allows the assumption that the outer flow is inviscid, which is the basis of most aerodynamic models.
1.5.2 Standard coefficients
For the description of aerodynamic flows, a convenient non-dimensional form of the pressure is the pressure coefficient Cp. This is equivalent to the dimensionless pressure variable p used in Section 1.5.2, except
that Cp is shifted by some reference pressure pref, and its normalizing dynamic pressure qref contains the traditional factor of 3.
Cp = ^ , 9ref = ^PrefK-ef (1-53)
qref
In external aerodynamics applications, the reference quantities are normally chosen to correspond to freestream
flow, pref — Рж, VTef — , pref — Рж,
p рж 1 2
Cp = ——————— , <?oo = ^ржУж (1.54)
Яж
so that in the freestream we have Cp — 0. Since Cp measures the deviation of the pressure from pref, it is unaffected by any constant offset in all the pressures.
The skin friction coefficient, which is a non-dimensional wall shear stress, is normalized the same way.
Cf = — (1.55)
f Яж
An alternative normalization which uses the local dynamic pressure at a specific surface location gives the local skin friction coefficient Cf, which is more natural in boundary layer theory and will be treated in Chapter 4.
Dimensionless coefficients which quantify aerodynamic forces and moments are also extensively used in aerodynamics. These will be introduced in Chapter 5.











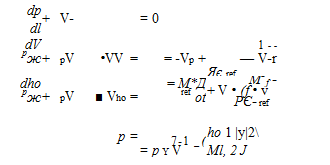


 pV, the integral mass equation (1.27) can be restated in terms of only a volume integral.
pV, the integral mass equation (1.27) can be restated in terms of only a volume integral.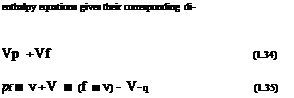 – Pt-
– Pt-