We have studied, so far, how high the temperatures can get at the stagnation point of a hypersonically flying vehicle because of a strong shock forming before the nose. At very high temperatures and low pressures of high altitudes, the chemical composition of air cannot remain the same. Before the chemical composition change, first the change in the specific heats with temperature occurs. Therefore, the air is no longer a calorically perfect gas. Since the change in the specific heats depends on the temperature, we can assume the air as a thermally perfect gas, and use the temperature dependent specific heat ratios instead of constant у = 1.4. On the other hand, the gas constant R has the same dependence on the specific heats both for the calorically or thermally perfect gas, i. e. cp — cv = R still holds.
At high temperatures, the temperature dependent behavior of the specific heats of the air can be determined with the aid of ‘gas kinetics’. The chemical composition of the air at normal conditions contains 79% molecular nitrogen N2, 20% molecular oxygen O2, and 1% other gases. In this composition, neglecting the other gases the air is mainly composed of molecular nitrogen and oxygen. For di-atomic gases, the internal energy of the molecule is composed of the translational and the rotational energies. This internal energy increases linearly with temperature, and is expressed as: e = etr + erot. Using statistical methods for di-atomic gases the translational energy depending on temperature T reads as ete = 3/2 RT, and the rotational energy becomes: erot = RT (Lee et al. 1973). This gives the total internal energy in terms of temperature, and the specific heat constant at constant volume as follows
5 Oe 5 , .
e = RT, cv = = R (7.69a, b)
2 v OT 2 v ;
At higher temperatures, temperatures above 800 K, the bond between the di-atomic molecules starts to vibrate to further increase the internal energy. This increase in the internal energy is called the vibration energy of a molecule. The change in the vibration energy of the molecule is non-linear with the temperature, and the classical thermodynamics is insufficient to calculate the temperature dependence of vibration energy. The quantum mechanical approach with the concept of partition function is necessary to express the vibration energy as follows (Appendix 8):
Here, h = 6.625 x 10 34 Js is the Planck constant, v is the fundamental frequency of the molecule, and k = 1.38 x 10-23 J/K is the Boltzmann constant. The fundamental frequencies for the nitrogen and the oxygen molecules are different, and they are for N2: vN2 = 7.06 x 1013s_ and for O2: vo2 = 4.73 x
1013s_ (Anderson 1989). Accordingly, the specific internal energy at high temperatures reads as
Hence, the derivative of the Eq. 7.71 with respect to temperature gives us the specific heat constant at constant volume with the following temperature dependence
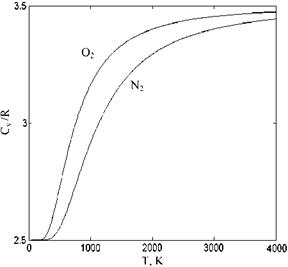
Shown in Fig. 7.18 is the variation of cv/R with temperature for the nitrogen and the oxygen molecules having vibrational energies.
According to Fig. 7.18, when 4,000 K is reached the value of cv/R approaches 7/2 as its limit value for di-atomic molecules. The limiting value of the exponential term in Eq. 7.72 approaches unity as temperature goes to infinity.
On the other hand, the classical statistical theory gives the value of vibrational energy as evib = RT which is true only for T approaching infinity. For the values of temperature which are of interest to us, the evaluation of vibration energy with classical theory is not correct. At temperatures above 2,000 K the oxygen molecules disassociate and above 4,000 K the same thing happens to the nitrogen molecules so that the chemical composition of the air changes, and the relevant chemical reactions must be include at such high temperatures. The necessary reaction energies for the partial or full disassociations of the species are provided by the aerodynamic heating generated by high speeds and the ambient pressure.
 |
 |
Under normal room pressure, the full disassociation of oxygen molecules is complete at 4,000 K, and the nitrogen molecules are fully disassociated at 9,000 K (Anderson 1989). The disassociation of molecules starts at smaller temperatures at low ambient pressures of high altitudes. At higher temperatures than 9,000 K, both oxygen and nitrogen atoms start to ionize. For this reason, it becomes necessary to construct a graphical representation for a hypersonic vehicle subjected to aerodynamic heating because of its high speed at different altitudes having different ambient pressure in which the continuum approach still holds, Fig. 7.19 (adapted from Riedelbauch et al. 1987; Anderson 1989).
According to Fig. 7.19, the vibration energy starts before the speed of 1 km s-1, and continues up to 2.6 km s-1 which is indicated by a solid vertical line. Above 3 km s-1, the oxygen molecules disassociate at sea level and disassociation starts at 2 km s-1 at high atmospheric levels. The range of oxygen disassociation, indicated with dashed dotted line, occurs between 3.2 and 6.5 km h-1, at the upper levels it happens at 2.0-5.0 km h-1. As the speed increases the nitrogen molecules disassociation range changes in the speed range of 6-10 km s-1, whereas this range drops down to 5-8 km s-1 at higher altitudes as shown with dashed vertical curves. At even higher speeds and altitudes higher than 20 km, the ionization of oxygen and nitrogen, as shown with a solid curve starts. This speed is above 10.5 km s-1 at the top levels of the atmosphere. Also shown in Fig. 7.19 is the approximate re-entry orbit of the space shuttle. According to this orbit, the shuttle cruises aerodynamically and ballistically in disassocited atoms with M = 28 at altitude of 100 km, and descends down to the 50 km altitude as its speed goes down to M = 8 while moving in air molecules full of vibrational energy. At the left side of the Fig. 7.19, shown with a single dashed curve is the approximate ascending path of the space shuttle. On its way up, the
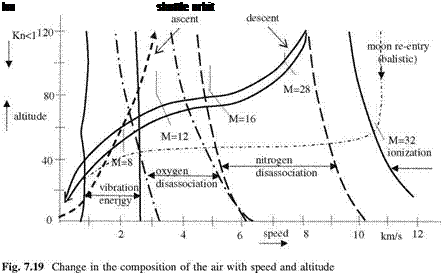 |
shuttle moves through the air molecules put into vibration by its motion, and after the altitude of 70 km it goes through a region of the atmosphere where the oxygen molecules are disassociated. After the level of 80 km the air is no longer continuous medium since the Knudsen number is above 0.1, and no-slip condition no longer prevails.
At the far right side of Fig. 7.19, shown is the path line of a space capsule, like Apollo capsule, making a re-entry at a speed of 11 km s-1 in an environment that consists of ionized oxygen and nitrogen atoms. The path of the capsule is totally ballistic, i. e., only the drag force is acting to slow it down. At altitude of 52 km, the capsule has a very high Mach number, M = 32, which creates a very strong shock to increase the temperature to the order of 9,000 K. Since the temperatures are sufficiently high, we can study the chemical reactions involved in the disas – sociation of air molecules assuming that the reactions are occurring in equilibrium, and can determine the relations for pressure, density and the temperature of the air which is no longer a perfect gas. Now, we write the law of mass action for each species involved in chemical reactions with equilibrium constants K and the stoichiometric coefficients depending on temperature (Denbigh 1978) as follows
|
O2 $
|
2O
|
Kp, O2 (T) =
|
(PO)2
PO2
|
(7.73a)
|
|
N2 $
|
2N
|
KpN2 (T) =
|
(PN)2
PN2
|
(7.73b)
|
|
N + O <
|
$ NO
|
Kp, NO (T)
|
_ PNO PNPO
|
(7.73c)
|
N + O $ NO+ + e – Kpnq+(T) = Pnq+Pe – (7.73d)
PnPo
Here, the total pressure p in terms of the partial pressures of six species is written as
p = po2 + Pn2 + Pn + Pq + Pnq + Pno+ + Pe – (7.73e)
Since the equilibrium constant for each specie involved in Eq. 7.73a is given in terms of the temperature, we can obtain the total pressure for a given temperature. We know the density from the solution of the continuity equation. Then, we can express the equation of state as a polynomial for the air at high temperatures in terms pressure, density and the temperature. There are various forms of these polynomials in open literature, however, we will be making use of the one which is prepared by Tannehill and Mugge and provided by Anderson for its convenient usage in our next example.
ExamPle 7.4 The re-entry speed of Apollo capsule is 11 km s-1 which corresponds to M = 32.2 at 52 km altitude. Compute the temperature behind the shock assuming (a) calorically perfect gas, (b) the chemical equilibrium is reached so that new equation of state can be used.
Solution: (a) Assuming calorically perfect gas and у = 1.4; from the temperature ratio we get To/T = 1 + (у — 1)/2M2 = 208. Here, the temperature before the shock at 52 km altitude T1 = T = 270.7 gives us T2 = To = 208 x 270.7 = 56,305 K! This temperature is so high and so wrong! Because, under these conditions the air is not calorically perfect and there is a considerable decrease in the temperature behind the shock because of energy used by the formation energy of the new species formed.
(b) The pressure and density ratios for after and before the shock are to be computed as p2/pi = 1,387 and p2/p1 = 15.19, respectively. In order for Tannehill and Munge’s polynomial approximations to be used at 52 km altitude we express the pressure and density with respect to sea level values. Accordingly, we find
p2/psl = p2/pj x pj /psl = 1,387 x 0.0007874 = 1.092 and P2/Ps = Pi/P x P/Ps = 15.19 x 0.0008383 = 0.01273
From those values and reading from the graph gives us T2/Tsl = 40 and T2 = 11,520 K. This gives us a more realistic temperature behind the shock. If we calculate the pressure behind the shock with equilibrium chemistry the result obtained with the calorically perfect gas does not change.
However, for the density there is a difference of 2.5-fold!
In the orbit of the re-entering capsule from moon mission shown in Fig. 7.19, argon is the only gas whose concentration, 1%, remains the same. Apart from this ionized nitrogen oxide, NO+, and electron, e—, molal concentrations do not exceed 10—3. This concentration affects the gas dynamic behavior insignificantly. However, the ionization amount is sufficient to destruct the electronical communication between the capsule and earth (Anderson 1989).
Another ballistic orbit is the re-entry path of the Mars mission, which lies outside of Fig. 7.19, and which has the approximate re-entry speed of 15 km s-1. The order of aerodynamic heating generated and problems created at this speed, naturally, require special design and analysis.
In order to obtain meaningful lift during the descent of the space shuttle, the flight path inside of the narrow enveloping curve shown in Fig. 7.19 must be followed. In the lower path of the enveloping curve the descent is fast and the lift is high to give m/(CLS) = 5,000 kg/m2, where m is the total mass, CL is the total lift and S is the lifting surface area of the shuttle. The upper route on the other hand gives m/(CLS) = 50 kg/m2. The actual intermediate path followed by the shuttle provides us approximately m/(CLS) = 500.
Obviously, the addition of chemical reactions and the equilibrium chemistry to the equations we consider further complicates the analysis, however, at high temperatures it provides us with more realistic solutions.
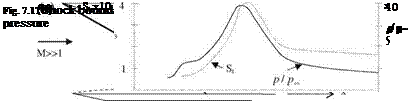
The difference between the solutions based on equilibrium chemistry and the calorically perfect gas assumption at high free stream Mach numbers at high altitudes not only yields different values for temperature and density but also it gives very different flow features and characteristics. Shown in Fig. 7.20 are the different shock locations in front of a circular cylinder which are obtained with the assumption of calorically perfect gas and with chemical equilibrium assumptions.
According to Fig. 7.20, the shock location obtained with the equilibrium chemistry is much closer to the body. Naturally, with the chemical reactions behind the shock, the composition of the air also changes. The changing composition of the air alters the total pressure and the gaseous properties of the air; therefore, the analysis needs to be aerothermochemical rather than aerothermo – dynamic. In addition, in our aerothermochemical analysis fast chemical composition changes may force us to resort to chemical kinetics which considers the non equilibrium chemistry in flow analysis. Now, we can calculate the shock position assuming different flow conditions in front of a blunt body.
So far we have seen the effect of the equilibrium chemistry on the air composition at high temperature in hypersonic flow. The equilibrium chemistry
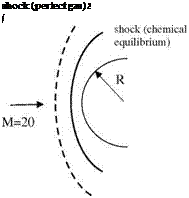 Fig. 7.20 At M = 20 free stream and 20 km altitude shock forming before a circular cylinder with assuming a perfect gas, b chemical equilibrium
Fig. 7.20 At M = 20 free stream and 20 km altitude shock forming before a circular cylinder with assuming a perfect gas, b chemical equilibrium
assumes that throughout the flow the composition of the air changes instantly under equilibrium. At high flow speeds there are two different procedures to determine the composition of the air. These assumptions are (1) frozen flow, and (2) flow under finite chemical rates.
In frozen flow, because of high speeds, the air molecules are assumed to continue to flow without undergoing chemical reaction. Because its composition does not change, the flow is assumed to be frozen. In reality, however, the chemical reactions take place with a finite rate that is the flow composition is between the frozen and the equilibrium chemistry. For this reason we resort to chemical kinetics, which deals with the chemical reactions happening with finite rates and finding the rates of reaction experimentally and/or theoretically. As we have done before, let us start from the vibrational energy of a diatomic gas like oxygen molecule O2 which becomes effective above 800 K. Equation 7.70 gave us the vibrational energy of a diatomic gas as follows
The physical model which explains the reason for the vibrational energies of diatomic gas molecules is the collision between the enough number of molecules as the temperature rises to make Eq. 7.74 to become active. In practice, however, the air molecules behind the shock do not start to vibrate immediately. There has to be some time to pass for a molecule to be in complete state of vibration. The previous vibration state of the molecule affects the vibrational energy of the molecule at current time t. Therefore, we need to model the time dependent vibrational energy change for the molecule with a first order differential equation as follows
Here, s is the relaxation time which depends on the pressure and the temperature of the air as follows (Vincenti and Kruger 1965).
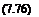 _ cexp(K2/T )1/3
_ cexp(K2/T )1/3
s — C
p
The values of C and K2 are determined experimentally. These values are provided for the oxygen, and nitrogen molecules for various temperature ranges by Vincenti and Kruger and summarized in Table 7.1.
|
Table 7.1 Relaxation time constants for vibration energies
|
Specie
|
C (atm-ps)
|
K2, K
|
Temperature range (K)
|
|
O2
|
5.42 x 10-5
|
2.95 x 106
|
800-3,200
|
|
N2
|
3.58 x 10-4
|
1.91 x 106
|
800-6,000
|
|
NO
|
4.86 x 10-3
|
1.37 x 105
|
1,500-3,000
|
|
On the other hand, the solution of the first order differential equation, Eq. 7.75, as an initial value problem with initial condition for the vibrational energy: evib = evo at t = 0 gives us the following
evib = eVib + (ev0 – eVib) exp(-t/x) (7.77)
According to Eq. 7.77, this simple physical model allows us to solve the time dependent vibration energy for the same specie with two different initial conditions. The first possibility is to start with an initial vibration energy which is smaller than the equilibrium vibration energy and to reach the equilibrium vibration energy. In this first case, during acceleration or ascending of the vehicle the temperature increases with the shock strength increase; therefore, the small value of the initial vibration energy increases to reach the equilibrium vibration energy. The second case, on the other hand, is encountered by a re-entering vehicle at very high temperatures, which makes the initial vibration energy higher than the equilibrium vibration energy which is reached by slowing down of the vehicle together with the decrease in temperature.
Now, we can analyze the time dependence of vibration energy given by Eq. 7.77 as a graph provided in Fig. 7.21. According to Fig. 7.21, in the case of re-entry very high speeds create very high temperatures with high initial vibration energy reaching its equilibrium by time. On the other hand, during ascend and before leaving the atmosphere the species around the vehicle first have low vibrational energy and with speed up process the ambient temperature rises and the equilibrium vibration energy is reached in time. Here, in both cases reaching the equilibrium vibration energy happens in micro seconds because of the character of the chemical reactions as demonstrated in the following example.
Example 7.5 Obtain the time dependent expression for the vibration energy of pure oxygen molecules at 1 atmosphere pressure and 3,000 K. Find the time elapsed for the difference between the initial vibration energy and the equilibrium vibration energy to drop to value of 1%.
Fig. 7.21 Time dependence of vibration energy
Solution: From Table 7.1 the relaxation time s = 1.13 x 10 6 s. Equation 7.77 the gives
e-t/s = 0.01
and,
t = 1.13 x 10-6 x 4.60 = 5.20 x 10-6s.
As seen in the example, the passage from higher energy levels to equilibrium energy level takes place in micro seconds. This means non equilibrium vibration energy changes take place 2 or 3 order of magnitude faster than the solution of unsteady flow equations. This in practice means that the one step time resolution of the unsteady flow solvers is more than enough to reach equilibrium in time dependent treatment of non equilibrium chemical reactions using chemical kinetics.
Now, we can look at the rate of chemical reactions taking place at high temperatures, and compare the differences between the results obtained for the flow field with equilibrium chemistry.
Previously, we have given the equilibrium chemistry equations, Eq. 7.73a, d used for air at high speeds. Now, we can construct a new set of equations in which catalyzing effects of M molecules will be used. In the reactions considered here the catalysis is possible either with the reacting molecules themselves, or molecules from outside can act as catalisors. When we give the chemical reactions for the air molecules, we also provide the relevant catalisors in the form of a table. Naturally, with the aid of different catalisors the chemical reaction speeds will be quite different. The following four reactions will take place with different catalyzing agents as follows
(1)

 dd°! = 2kf 1 [O2][M]- 2kb1 [O]2[M] ^N1 = 2kf2 [N2][M]- 2kb2[N]2[M] d[NO! = kf 3 [N][O][M]- kb3 [NO][M] ®+] = kf4 [N][O]- kb4 [NO+]
dd°! = 2kf 1 [O2][M]- 2kb1 [O]2[M] ^N1 = 2kf2 [N2][M]- 2kb2[N]2[M] d[NO! = kf 3 [N][O][M]- kb3 [NO][M] ®+] = kf4 [N][O]- kb4 [NO+]

The coefficients kf and kb, the forward and backward reaction rate coefficients of Eq. 7.78a-d are obtained experimentally. In addition, in reactions ranging from (1) to (3), the different M atoms working as catalisor provide different reaction rate coefficients. For only Eq. 1, we can write five different equations. That is in order to obtain 2O; N, NO, O, O2 and N2 get into chemical reaction with O2. Similarly, in order to obtain 2N, reaction (2) has to undergo 5 different sub reactions, and to get NO, reaction (3) must undergo three different sub reactions.
Now, let us see how the reaction rate coefficients are calculated. The proper Arrhenius equation for the forward reactions depending on temperature T can be written (Vincenti and Kruger 1965) as follows
kf = CfT^f exp (-Kf /kT) (7.79)
Using the Vincenti and Kruger’s data, the reaction constants for reaction (1) to (4) are provided in Table 7.2
Now, we can plot the forward reaction rates for chemical reactions (1) and (3) in terms of temperature given at Table 7.2, Fig. 7.22. According to the graphs in Fig. 7.22, formation speed of 2O from O2 becomes different from the formation speed of nitrogen oxide from oxygen and nitrate above 3,500 K. At 5,000 K, this difference is as high as one order of magnitude. This means, at high temperatures the disassociation of oxygen molecules is much faster compared to the production of nitrogen oxide from disassociated oxygen and nitrogen if reactions (1) and (3) are considered alone.
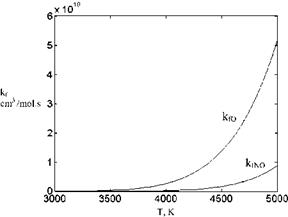 Fig. 7.22 Comparison of the forward reaction rates of dis – association of oxygen with formation of nitrogen oxide
Fig. 7.22 Comparison of the forward reaction rates of dis – association of oxygen with formation of nitrogen oxide
As we give the type of reactions with Eqs. 7.78a-d, we also give the relevant forward and backward reaction rates. The Arhenius equation, Eq. 7.79, is the formula to be used to calculate the forward reaction rate. Backward reaction rates, kb, on the other hand, can be found from equilibrium chemistry. If we write the concentrations at chemical equilibrium using Eq. 7.78a, in terms Kp we obtain
Now, we can use Eq. 7.80 in Eq. 7.78a to get
For the remaining reactions the backward reaction rates can be obtained similarly.
Now, let us formulate the one dimensional reacting flow with chemical kinetics as the simplest flow case. Let Mt be the molal weight of specie in chemical reaction. The mass rate of the same specie will be given by the aid of Eq. 7.81 as Wi = Mj-jjli. The same specie has its partial density, pt, change with the flow velocity in terms of the continuity equation as follows
0pi/0t + O(piu)/Ox = wi (7.82a)
The total sum of partial densities of the species gives the average density of air ^2 Pi = p. In terms of the mass fraction of the species c, = pjp, Eq. 7.82b
i
becomes
0ci/0t + ubci/Ox = Wi / p (7.82b)
In addition, the vibration energy in terms of mass fraction reads as
0cievib/0t + u0(cievib)/0x = ci(elqb – evib)/s (7.83)
The governing equations: continuity, momentum, and energy equations then, respectively, read as
|
0p/0t + 0(pu)/0x = 0
|
(7.84)
|
|
pOu/Ot + Op/Ox + pu0u/0x = 0
|
(7.85)
|
|
pOe/Ot + pOu/Ox + puOe/Ox = 0
|
(7.86)
|
Here, e is the total internal energy and, p is the total pressure. The relaxation time s of the chemical kinetics is used as a constraint in time discretization. During numerical solution, the time step must be one order of magnitude less than the value of s predicted for that time step.
|
Speed, km s 1
|
Alt. km
|
Shock radius, m
|
Chem kin
|
Equilb. chem.
|
Frozen Flw. Ideal Flw
|
|
5
|
66
|
0.33
|
0.0676
|
0.0625
|
0.089 0.113
|
|
7.5
|
66
|
0.21
|
0.0666
|
0.0461
|
0.0805 0.108
|
|
Table 7.3 Shock distance for different air models
|
|
Non dimensional shock distance, d/Rs
|
In this way, we can model the fastest changing energy in the time dependent reacting flow. Here, the time step taken can be very small, the reactions may take place very fast, and the reaction rate coefficients can be very large to make the differential equations ‘stiff’. We have to resort to special numerical solution techniques for the stiff differential equations (Hoffman 1992).
The system of differential equation 7.82-a-7.86 solved with the proper initial conditions gives us q, u and e values and also c, and the vibration energy of ith specie. The temperature T of the medium can be found from ^,с, е = e relation as follows
Here (Ahf)°is the effective reference energy of the specie i, and is known as the heat of formation of specie i. The heat of formation for each specie can be obtained from JANAF (Joint Army Navy Air Force) tables.
Now, we can see the two dimensional application of the theory on a blunt body with addition of 16 species equation added to Eq. 7.78a for calculating the flow field interacting with chemical kinetics (Hall et al. 1962). Hall et al. used the theory on flow about the sphere, and compared the solutions with the ideal flow solutions obtained at different altitudes and free stream conditions. The results obtained are compared in Table 7.3 for two different free stream speeds at the same altitude.
According to Table 7.3, chemical kinetics give the shortest shock distance. The time dependent reactions put the shock a little further from the body, the frozen flow pushes the shock even further. The ideal flow solution gives the maximum shock-body distance.
![]()
![]()
![]()
![]()
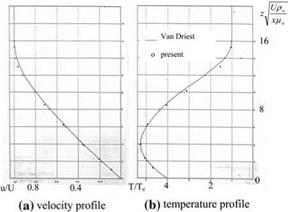
 done with Eq. 7.90a, b at x/R = 0, and the boundary layer edge to wall velocity ratio is taken as 2 for temperature profiles where the wall appears to be cold.
done with Eq. 7.90a, b at x/R = 0, and the boundary layer edge to wall velocity ratio is taken as 2 for temperature profiles where the wall appears to be cold.












 Fig. 7.20 At M = 20 free stream and 20 km altitude shock forming before a circular cylinder with assuming a perfect gas, b chemical equilibrium
Fig. 7.20 At M = 20 free stream and 20 km altitude shock forming before a circular cylinder with assuming a perfect gas, b chemical equilibrium

 Fig. 7.22 Comparison of the forward reaction rates of dis – association of oxygen with formation of nitrogen oxide
Fig. 7.22 Comparison of the forward reaction rates of dis – association of oxygen with formation of nitrogen oxide


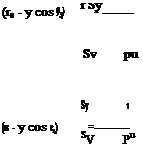
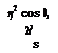
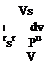
 M
M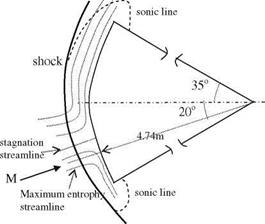 Fig. 7.9 Hypersonic flow
Fig. 7.9 Hypersonic flow rinted with permission of the American Institute of Aeronautics and Astronautics’’
rinted with permission of the American Institute of Aeronautics and Astronautics’’

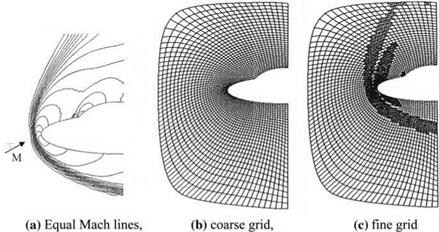
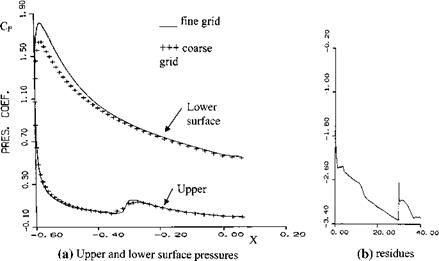
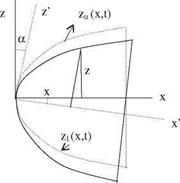
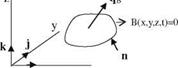 Fig. 7.5 Body B(x, y,z, t) = 0 z n„
Fig. 7.5 Body B(x, y,z, t) = 0 z n„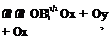 IgradB|
IgradB|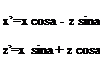
 it is possible to obtain the stagnation pressure to be used in Eq. 7.7 (see Problem 7.1). Improved Newton formula gives good results for the high angle of attack flows with high wall angles. Shown in Fig. 7.2a is the parabolic surface given by x = 0.729y2 — 1.0, and in Fig. 7.2b is the surface pressure coefficient plots obtained by Newton and improved Newton formula at M = 8.
it is possible to obtain the stagnation pressure to be used in Eq. 7.7 (see Problem 7.1). Improved Newton formula gives good results for the high angle of attack flows with high wall angles. Shown in Fig. 7.2a is the parabolic surface given by x = 0.729y2 — 1.0, and in Fig. 7.2b is the surface pressure coefficient plots obtained by Newton and improved Newton formula at M = 8.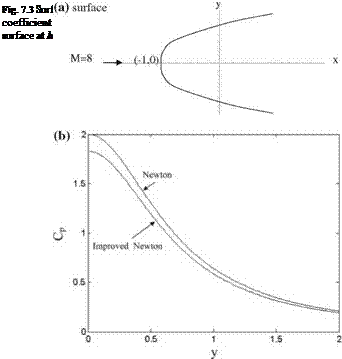
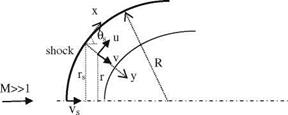
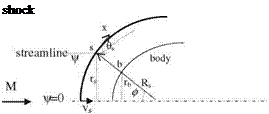
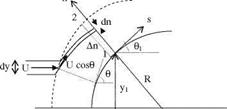 where s is the tangential and n is the normal coordinates. The centripetal force acting in a unit volume is pV2/R where V shows the flow speed and 1/R shows the radius of curvature. The pressure force gradient which balances the centripetal force can be written as
where s is the tangential and n is the normal coordinates. The centripetal force acting in a unit volume is pV2/R where V shows the flow speed and 1/R shows the radius of curvature. The pressure force gradient which balances the centripetal force can be written as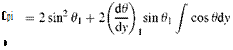
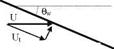 Fig. 7.1 Velocity components of the fluid particles impinging on a wall at a free stream speed of U
Fig. 7.1 Velocity components of the fluid particles impinging on a wall at a free stream speed of U