“Aeroelasticity” is the term used to denote the field of study concerned with the interaction between the deformation of an elastic structure in an airstream and the resulting aerodynamic force. The interdisciplinary nature of the field is best illustrated by Fig. 1.1, which originated with Professor A. R. Collar in the 1940s. This triangle depicts interactions among the three disciplines of aerodynamics, dynamics, and elasticity. Classical aerodynamic theories provide a prediction of the forces acting on a body of a given shape. Elasticity provides a prediction of the shape of an elastic body under a given load. Dynamics introduces the effects of inertial forces. With the knowledge of elementary aerodynamics, dynamics, and elasticity, students are in a position to look at problems in which two or more of these phenomena interact. The field of flight mechanics involves the interaction between aerodynamics and dynamics, which most undergraduate students in an aeronautics/aeronautical engineering curriculum have studied in a separate course by their senior year. This text considers the three remaining areas of interaction, as follows:
• between elasticity and dynamics (i. e., structural dynamics)
• between aerodynamics and elasticity (i. e., static aeroelasticity)
• among all three (i. e., dynamic aeroelasticity)
Because of their importance to aerospace system design, these areas are also appropriate for study in an undergraduate aeronautics/aeronautical engineering curriculum. In aeroelasticity, one finds that the loads depend on the deformation (i. e., aerodynamics) and that the deformation depends on the loads (i. e., structural me – chanics/dynamics); thus, one has a coupled problem. Consequently, prior study of all three constituent disciplines is necessary before a study in aeroelasticity can be undertaken. Moreover, a study in structural dynamics is helpful in developing concepts that are useful in solving aeroelasticity problems, such as the modal representation.
It is of interest that aeroelastic phenomena played a major role throughout the history of powered flight. The Wright brothers utilized controlled warping of the wings on their Wright Flyer in 1903 to achieve lateral control. This was essential to their success in achieving powered flight because the aircraft was laterally unstable due to the significant anhedral of the wings. Earlier in 1903, Samuel Langley made
|
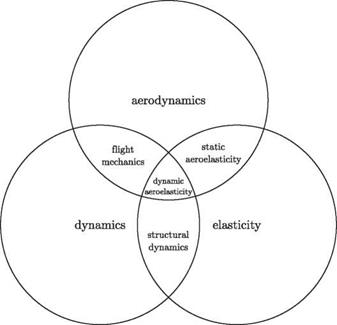
Figure 1.1. Schematic of the field of aeroelasticity
|
two attempts to achieve powered flight from the top of a houseboat on the Potomac River. His efforts resulted in catastrophic failure of the wings caused by their being overly flexible and overloaded. Such aeroelastic phenomena, including torsional divergence, were major factors in the predominance of the biplane design until the early 1930s, when “stressed-skin” metallic structural configurations were introduced to provide adequate torsional stiffness for monoplanes.
The first recorded and documented case of flutter in an aircraft occurred in 1916. The Handley Page O/400 bomber experienced violent tail oscillations as the result of the lack of a torsion-rod connection between the port and starboard elevators—an absolute design requirement of today. The incident involved a dynamic twisting of the fuselage to as much as 45 degrees in conjunction with an antisymmetric flapping of the elevators. Catastrophic failures due to aircraft flutter became a major design concern during the First World War and remain so today. R. A. Frazer and W. J. Duncan at the National Physical Laboratory in England compiled a classic document on this subject entitled, “The Flutter of Aeroplane Wings” as R&M 1155 in August 1928. This small document (about 200 pages) became known as “The Flutter Bible.” Their treatment for the analysis and prevention of the flutter problem laid the groundwork for the techniques in use today.
Another major aircraft-design concern that may be classified as a static – aeroelastic phenomenon was experienced in 1927 by the Bristol Bagshot, a twin – engine, high-aspect-ratio English aircraft. As the speed was increased, the aileron effectiveness decreased to zero and then became negative. This loss and reversal of aileron control is commonly known today as “aileron reversal.” The incident was successfully analyzed and design criteria were developed for its prevention by Roxbee Cox and Pugsley at the Royal Aircraft Establishment in the early 1930s. Although aileron reversal generally does not lead to a catastrophic failure, it can be dangerous and therefore is an essential design concern. It is of interest that during this period of the early 1930s, it was Roxbee Cox and Pugsley who proposed the name “aeroelasticity” to describe these phenomena, which are the subject of this text.
In the design of aerospace vehicles, aeroelastic phenomena can result in a full spectrum of behavior from the near benign to the catastrophic. At the near-benign end of the spectrum, one finds passenger and pilot discomfort. One moves from there to steady-state and transient vibrations that slowly cause an aircraft structure to suffer fatigue damage at the microscopic level. At the catastrophic end, aeroelastic instabilities can quickly destroy an aircraft and result in loss of human life without warning. Aeroelastic problems that need to be addressed by aerospace system designers can be mainly static in nature—meaning that inertial forces do not play a significant role—or they can be strongly influenced by inertial forces. Although not the case in general, the analysis of some aeroelastic phenomena can be undertaken by means of small-deformation theories. Aeroelastic phenomena may strongly affect the performance of an aircraft, positively or negatively. They also may determine whether its control surfaces perform their intended functions well, poorly, or even in the exact opposite manner of that which they are intended to do. It is clear then that all of these studies have important practical consequences in many areas of aerospace technology. The design of modern aircraft and space vehicles is characterized by the demand for extremely lightweight structures. Therefore, the solution of many aeroelastic problems is a basic requirement for achieving an operationally reliable and structurally optimal system. Aeroelastic phenomena also play an important role in turbomachinery, in wind-energy converters, and even in the sound generation of musical instruments.
The most commonly posed problems for the aeroelastician are stability problems. Although the elastic moduli of a given structural member are independent of the speed of the aircraft, the aerodynamic forces strongly depend on it. It is therefore not difficult to imagine scenarios in which the aerodynamic forces “overpower” the elastic restoring forces. When this occurs in such a way that inertial forces have little effect, we refer to this as a static-aeroelastic instability—or “divergence.” In contrast, when the inertial forces are important, the resulting dynamic instability is called “flutter.” Both divergence and flutter can be catastrophic, leading to sudden destruction of a vehicle. Thus, it is vital for aircraft designers to know how to design lifting surfaces that are free of such problems. Most of the treatment of aeroelasticity in this text is concerned with stability problems.
Much of the rest of the field of aeroelasticity involves a study of aircraft response in flight. Static-aeroelastic response problems constitute a special case in which inertial forces do not contribute and in which one may need to predict the lift developed by an aircraft of given configuration at a specified angle of attack or determine the maximum load factor that such an aircraft can sustain. Also, problems
of control effectiveness and aileron reversal fall in this category. When inertial forces are important, one may need to know how the aircraft reacts in turbulence or in gusts. Another important phenomenon is buffeting, which is characterized by transient vibration induced by wakes behind wings, nacelles, or other aircraft components.
All of these problems are treatable within the context of a linear analysis. Mathematically, linear problems in aeroelastic response and stability are complementary. That is, instabilities are predictable from examining the situations under which homogeneous equations possess nontrivial solutions. Response problems, however, are generally based on the solution of inhomogeneous equations. When the system becomes unstable, a solution to the inhomogeneous equations ceases to exist, whereas the homogeneous equations and boundary conditions associated with a stable conguration do not have a nontrivial solution.
Unlike the predictions from linear analyses, in actual aircraft, it is possible for self-excited oscillations to develop, even at speeds less than the flutter speed. Moreover, large disturbances can “bump” a system that is predicted to be stable by linear analyses into a state of large oscillatory motion. Both situations can lead to steady – state periodic oscillations for the entire system, called “limit-cycle oscillations.” In such situations, there can be fatigue problems leading to concerns about the life of certain components of an aircraft as well as passenger comfort and pilot endurance. To capture such behavior in an analysis, the aircraft must be treated as a nonlinear system. Although of great practical importance, nonlinear analyses are beyond the scope of this textbook.
The organization of the text is as follows. The fundamentals of mechanics are reviewed in Chapter 2. Later chapters frequently refer to this chapter for the formulations embodied therein, including the dynamics of particles and rigid bodies along with analyses of strings and beams as examples of simple structural elements. Finally, the behavior of single-degree-of-freedom systems is reviewed along with a physically motivated discussion of stability.
To describe the dynamic behavior of conventional aircraft, the topic of structural dynamics is introduced in Chapter 3. This is the study of dynamic properties of continuous elastic configurations, which provides a means of analytically representing a flight vehicle’s deformed shape at any instant of time. We begin with simple systems, such as vibrating strings, and move up in complexity to beams in torsion and finally to beams in bending. The introduction of the modal representation and its subsequent use in solving aeroelastic problems is the main emphasis of Chapter 3. A brief introduction to the methods of Ritz and Galerkin is also included.
Chapter 4 addresses static aeroelasticity. The chapter is concerned with static instabilities, steady airloads, and control-effectiveness problems. Again, we begin with simple systems, such as elastically restrained rigid wings. We move to wings in torsion and swept wings in bending and torsion and then finish the chapter with a treatment of swept composite wings undergoing elastically coupled bending and torsional deformation.
Finally, Chapter 5 discusses aeroelastic flutter, which is associated with dynamic – aeroelastic instabilities due to the mutual interaction of aerodynamic, elastic, and inertial forces. A generic lifting-surface analysis is first presented, followed by illustrative treatments involving simple “typical-section models.” Engineering solution methods for flutter are discussed, followed by a brief presentation of unsteady – aerodynamic theories, both classical and modern. The chapter concludes with an application of the modal representation to the flutter analysis of flexible wings, a discussion of the flutter-boundary characteristics of conventional aircraft, and an overview of how structural dynamics and aeroelasticity impact flight tests and certification. It is important to note that central to our study in the final two chapters are the phenomena of divergence and flutter, which typically result in catastrophic failure of the lifting surface and may lead to subsequent destruction of the flight vehicle.
An appendix is included in which Lagrange’s equations are derived and illustrated, as well as references for structural dynamics and aeroelasticity.
Although to penetrate into the intimate mysteries of nature and thence to learn the true causes of phenomena is not allowed to us, nevertheless it can happen that a certain fictive hypothesis may suffice for explaining many phenomena.
—Leonard Euler
As discussed in Chapter 1, both structural dynamics and aeroelasticity are built on the foundations of dynamics and structural mechanics. Therefore, in this chapter, we review the fundamentals of mechanics for particles, rigid bodies, and simple structures such as strings and beams. The review encompasses laws of motion, expressions for energy and work, and background assumptions. The chapter concludes with a brief discussion of the behavior of single-degree-of-freedom systems and the notion of stability.
The field of structural dynamics addresses the dynamic deformation behavior of continuous structural configurations. In general, load-deflection relationships are nonlinear, and the deflections are not necessarily small. In this chapter, to facilitate tractable, analytical solutions, we restrict our attention to linearly elastic systems undergoing small deflections—conditions that typify most flight-vehicle operations.
However, some level of geometrically nonlinear theory is necessary to arrive at a set of linear equations for strings, membranes, helicopter blades, turbine blades, and flexible rods in rotating spacecraft. Among these problems, only strings are discussed herein. Indeed, linear equations of motion for free vibration of strings cannot be obtained without initial consideration and subsequent careful elimination of nonlinearities.
The treatment goes beyond material generally presented in textbooks when it delves into the modeling of composite beams. By virtue of the inclusion of this section, readers obtain more than a glimpse of the physical phenomena associated with these evermore pervasive structural elements to the point that such beams can be treated in a simple fashion suitable for use in aeroelastic tailoring (see Chapter 4). The treatment follows along with the spirit of Euler’s quotation: in mechanics, we seek to make certain assumptions (i. e., fictive hypotheses) that although they do not necessarily provide knowledge of true causes, they do afford us a mathematical
model that is useful for analysis and design. The usefulness of such models is only as good as can be validated against experiments or models of higher fidelity. For example, defining a beam as a slender structural element in which one dimension is much larger than the other two, we observe that many aircraft wings do not have the geometry of a beam. If the aspect ratio is sufficiently large, however, a beam model may suffice to describe the overall behavioral characteristics of a wing.
„ m 1
(2.10)
K = K(fb f2, Із, • • •)
