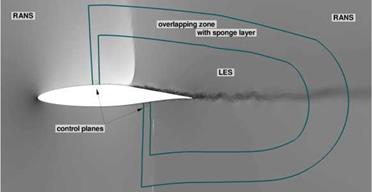
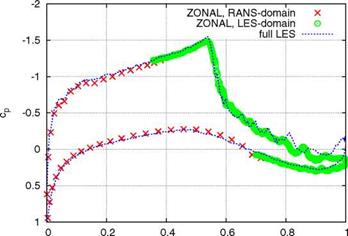
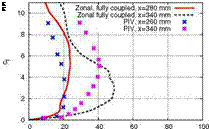
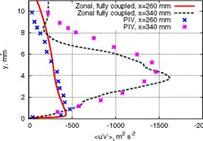
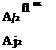The Method of Iterated Defect Correction
The defect correction approach was originally proposed by Zadunaisky ([22], [23]) for the estimation of the global discretization error in ordinary differential equations. The method was then generalized by Stetter [18] who introduced the iterative procedure which is applied in this work to partial differential equations. A number of theoretical investigations were done for ordinary differential equations by Frank ([5], [6]). Further papers of Pereyra ([15], [14]) show a different way of applying the defect correction method and gives additional analysis of the method. A nice overview on the defect correction approach can be found in Stetter [19] where he gives an overview of the different procedures. The proposed iterative defect correction method in this work is based on the procedure introduced by Stetter in [18] for ordinary differential equations. As was shown by Frank and Ueberhuber in [7] the iterated defect correction can also be applied on partial differential equations.
For the sake of simplicity we describe in the following the employed iterated defect correction on the example of a scalar one dimensional evolution equation
Mt + f {M)x = (1)
keeping in mind that the whole procedure can be extended to multi dimensions and to diffusion fluxes which additionally depend on Vm, as it is the case for the Navier-Stokes equations. As mentioned before, we focus on steady solutions, i. e., ut = 0. The time dependence in (1) is used only for the iteration of the approximate solution to a steady state. Conform with the convention in the cited papers we write the equation (1) in the abstract form
where the operator L is the exact linear or nonlinear differential operator and Lh is the discretized operator with the mesh width parameter h. For Lh we impose a stable, consistent and fast invertible operator, which is easily achieved by an operator with a low consistency order of one or two. For the theory of the iterated defect correction the operator Lh can also be of higher order. For practical calculations it is more interesting to correct a first or second order accurate method which is often applied in practice. Equation (2) will be called the basis method with the solution uh computed by inversion of the operator Lh:
Mh = L-1rh. (3)
Additionally we need another numerical method for the original problem (1) on the same mesh, but with a higher consistency order
![]() ShWh = rh-
ShWh = rh-
(4) . This higher order discretization will only be used to estimate the local defect and is applied once per defect iteration in that form. Instead of solving directly the higher order discrete problem which may need a lot of time and development of the solution procedure, the modified problem
LhMh rh dh (5)
is solved using the basic method (2). With dh = Shwh – Lhuh the local defect we apply equation (5) iteratively
LhM[k+1]= rh – df+1] k = 1,2,3,… ,NiDeC (6)
with the defect iteration index k and NIDeC the maximum defect correction iterations, converging towards the solution wh, the reconstruction polyomial higher order. The whole defect correction procedure can be formulated in the following step by step description.
1.
We start with a steady solution
of our basic method (2). The approximated solution uh is then reconstructed with the weighted essentially non oscillatory scheme, which will be described in sec-
[k]
tion 3. The reconstruction produces a polynomial distribution wlh of the integral average in each grid cell.
2. Applying now the operator of higher order consistency Sh to the reconstructed
[k] [k+1]
![The Method of Iterated Defect Correction Подпись: [ k] [ k] Shwh Lhuh 7 [ k] rh- dlh ■](/img/3129/image224_1.gif) |
|||
solution wh we compute the local defect dlh J for the next defect correction iteration k +1:
3. This defect is then subtracted as a source term on the right hand side of equation
(2) and the modified equation
Lhuhk+1]= rh – df+1] (9)
= rh – (Shwh – Lhuf^
is solved with the basic method, applying the inverse operator Lh-1. One gets then the corrected solution uhk+1] after the k-th defect iteration, converging for
Lhul+l]« Lhuf. (10)
With this convergence criteria, equation (9) reduces to the method higher order (4), with wh the reconstruction polynomial.
Equation (5) is also called the "neighboring problem" with respect to the original formulation of the defect correction by Zadunaisky. For the process of iterated defect correction one must assume that (6) and (2) are neighboring mathematical problems. Since wh represents a polynomial reconstruction of the basic solution uh on the same mesh, the defect dh as defined in equation (8) is "small" and so the assumption of the "neighboring problem" is plausible.
As we use a finite volume scheme for the basic method we can write the modified equation (5) in a semi discrete form defined on the interval, xj+i]x[ftn +At] with u = uh, being the discrete state in the cell i, as
tn+Atxi+1/2
![]() R(Qi) = j J f (Qi)xdxdt,
R(Qi) = j J f (Qi)xdxdt,
tn xi-1 /2
whereas Qi is considered as a placeholder for uf u[k+1] and wf^. As common for a finite volume approach the unknown physical flux f (Qi) is replaced by an appropriate numerical flux approximation g. і on the cell border of two adjacent cells. The numerical flux depends only on the states left and right of the cell interface:
g.+1 = #(=£?“ і, і), with defining the state on the interface in the cell itself
and Q+ being the state on the interface in the neighboring cell. If we choose as a simple example a basic method of first order in time and space, equation (11) yields
[k+i],+ )^_dk+i] (13)
with
At f , [k]
![]() — Spli
— Spli
an approximation of the corrected state uf+1] in the cell i. We point out that the
integral of the higher order fluxes f (wf) have to be computed with an appropriate numerical integration of accuracy higher than the one of the basic method. In the case of 1D there is no need of such an integration, the interface being the only integration point. For 2D or 3D discretizations an efficient integration scheme is necessary. In our case we use Gauss quadrature. This leads to an approximation of the flux integral in cell i as
where noP and rnj denote the number and the weights of the Gauss integration points j on the interface K, respectively, SK is the length or the surface and nK is the outward pointing unit normal vector. If the polynomial degree of the reconstruction is chosen to be p’ > p, with p, being the polynomial degree of the basic method, we take nop = p-^- for the 2D case, which is accurate up to a polynomial degree of p’. In the 3D case we use a rather sub-optimal number hgp = (p^)2 of Gauss points which is nevertheless accurate up to a polynomial degree p’.











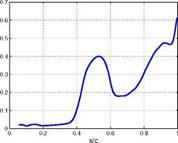
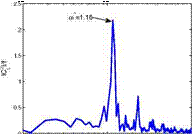
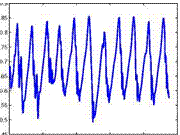
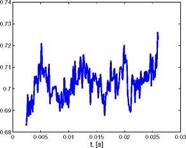
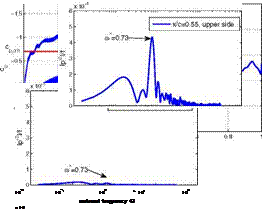


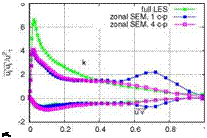
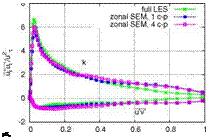
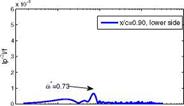 – x/c=0.90, upper side I
– x/c=0.90, upper side I