Sensor Controlled Zonal RANS-LES Method
Benedikt Roidl, Matthias Meinke, and Wolfgang Schroder
Abstract. A sensor was developed to detect aerodynamic regions in the computational domain of aerodynamic relevant flows where a common RANS simulation does no longer provide physically reliable results. These regions of the computational domain were then treated with a higher order turbulence model to suppress the modeling error being introduced by standard turbulence models inherent to RANS simulations. The sensor evaluates flow characteristics such as pressure gradients, Reynolds shear stress, and wall shear stress to detect model susceptible regions and to decompose the flow domain in RANS and LES regions. The subsequent approximate integration is performed by a zonal RANS/LES approach which combines the various RANS and LES areas. The sensor and the zonal method are validated by computing the flow over a flat plate, a shock boundary-layer interaction case and a transonic flow over an airfoil.
1 Introduction
To efficiently and accurately determine turbulent flows is still one of the major challenges in computational fluid dynamics. To develop a turbulence model which on the one hand is simple enough to allow an efficient solution and on the other hand, is general and susceptible to describe highly intricate flow phenomena sounds like a contradiction. Numerous classes of turbulence models (algebraic-, one-, two – equation-, RS-models) have been developed until today since the exact description of rotational, fully three-dimensional and time dependent flow is highly complex.
The introduction of the Reynolds averaging process to the Navier-Stokes equations presents the first step of simplification. The complete time-averaged
Benedikt Roidl • Matthias Meinke • Wolfgang Schroder Institute of Aerodynamics, RWTH Aachen University, WullnerstraBe 5a, 52062 Aachen, Germany e-mail: b. roidl@aia. rwth-aachen. de http://www. aia. rwth-aachen. de
B. Eisfeld et al. (Eds.): Management & Minimisation of Uncert. & Errors, NNFM 122, pp. 101-126. DOI: 10.1007/978-3-642-36185-2_5 © Springer-Verlag Berlin Heidelberg 2013
equation of the Reynolds stress tensor consists of different terms describing local and convective parts, production due to the Reynolds stress tensor, dissipation, pressure shear-correlation and diffusion [27]. A closed solution of these transport equations is not possible since they also consist of unknown correlation functions. Thus, semi-empirical equations for turbulent closure are employed. Simplifying the complete contracted time averaged balance equation for boundary layers decreases its complexity since the pressure shear correlation and higher-order terms vanish. This presents a significant simplification of the transport equations. When the second – order normal stress contribution in the production terms and the viscosity linked contributions to the dissipation terms are neglected the final simplified form of the transport equation for the kinetic energy is derived.
The simplifications mentioned above which are applied in one – and two-equation turbulence models will not give a physical answer in complex flows independent of the corresponding discretization level or grid quality. For this reason a higher order turbulence model has to be employed. It can be stated that by applying turbulence models – algebraic, one-equation, two-equation or Reynolds stress models – which include a higher order Boussinesq ansatz – no generally valid trend can be given concerning the prediction quality of specific flow phenomena such as flow separation and reattachment in aerodynamic applications. Moreover, the insufficient quality of the transition prediction constitutes another major uncertainty. A correlation between the quality of turbulence modeling and the variation of flow parameters cannot be provided in a general sense.
These general requirements and limitations in turbulence modeling restrict the applicability of RANS/URANS-methods to simple flow structures. The simulation of attached airfoil flow gives reliable results on skin friction and and pressure distributions, however, when high frequency transient flow phenomena occur the quality of the results is questionable. This was the motivation for the development of a sensor which is capable of detecting flow regions of a RANS simulation, where the reliability of the quality of the solution cannot be ensured. In these very regions, a higher order turbulence modeling is necessary leading to the idea of a zonal RANS – LES approach [9].
The development of this sensor requires an exact knowledge of possible physical errors in RANS turbulence models. In this study a sensor was developed to identify the flow regions where RANS simulations produce inaccurate results. These identified flow regions can be treated by a zonal RANS-LES approach.
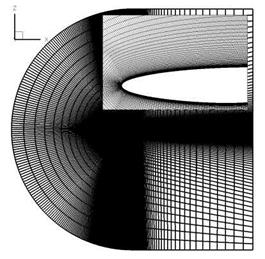
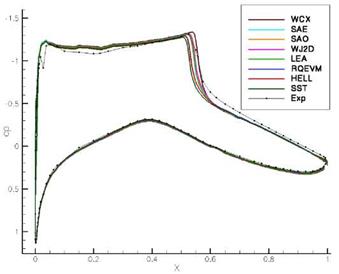
The article is organized as follows: In section 2, the numerical methods of the flow solver, the sensor and synthetic turbulence generation methods (STGM) are described. Subsequently, in section 3 the results are presented. First, the sensor is validated for three different flows and the susceptibility to critical parts of the sensor is discussed. Then, the various STGM are compared for different configurations in zero-pressure gradient boundary layers. Finally, the fully coupled zonal RANS-LES approach is compared with corresponding full domain LES and RANS solutions for two different cases. First, the case where an oblique shock impinging on a compressible turbulent boundary layer of a flat plate, i. e. the classical shock boundary-layer
interaction problem, is discussed. Second, a transonic flow over an airfoil causing buffet is considered.













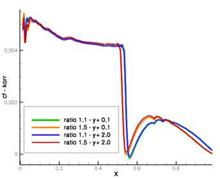
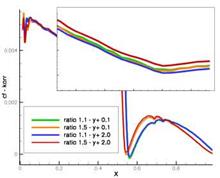
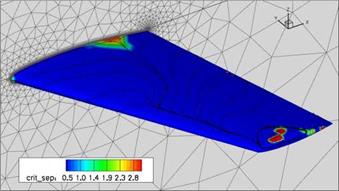

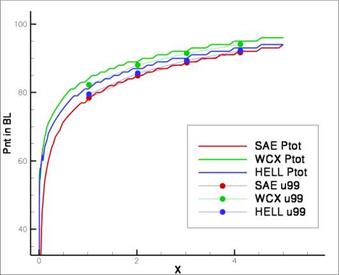
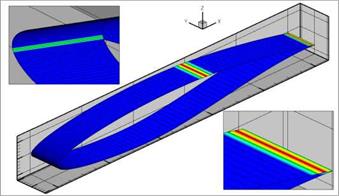
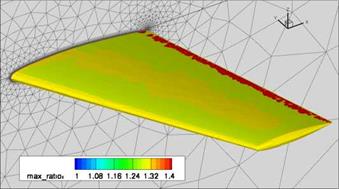



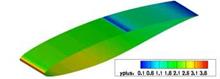

 After activation of the best practice output and declaration of the directory containing the configuration files of the best practice guidelines, the functionality of the individual sensors can be switched on and off. The configuration files are necessary to estimate the errors in the friction coefficients depending on the used model. These files contain a parameterized form of the error function as a polynomial 3rd order
After activation of the best practice output and declaration of the directory containing the configuration files of the best practice guidelines, the functionality of the individual sensors can be switched on and off. The configuration files are necessary to estimate the errors in the friction coefficients depending on the used model. These files contain a parameterized form of the error function as a polynomial 3rd order