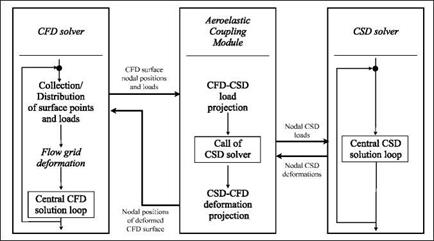
Moving-Least-Squares Interpolation (MLS)
The MLS interpolation method was first applied to spatial coupling in aeroelasticity by Quaranta et al. [23]. It exclusively uses low-order polynomials
s(x) = mT (x) a (11)
to approximate the spatial deformation distribution u(X). At each CFD surface point X, a new set of Q polynomial coefficients a(X) is computed with a moving least – squares fit. The Ng closest support points Xn provide a compact support; their influence relative to the CFD surface point is weighted with Wendland RBF (8). For each surface point X and its Ng support points inside the support radius g a functional
I(X, Xn)= 0(X, Xn) (mT (Xn) a(X) – Ux(X-n))2 dn(Xn) (12)
%
![Moving-Least-Squares Interpolation (MLS) Подпись: [m(Xn)] Ф(^, Xn) "v" =B](/img/3129/image326_1.gif) |
||||
has to be minimised for the coefficients a(X). The discrete form of this functional is reduced to the normal equation through a variation of coefficients ga:
Herein, Ф(X, Xn) = E |0(X, Xn)} is the diagonal matrix of RBF weighting factors. Inserting the interpolation function (11) yields
ux(X)= mT(X) A-1B [ux(Xn)} . (14)
‘—— V—— ‘
=P(X)
The row matrix P(X) describes the projection between a single surface point X and the Ng support points inside the support radius. Other than in the GSB method, in the MLS method the projection matrix is built row by row for each surface point separately. The final projection matrix P is assembled from the M row matrices of all surface points. For each surface point a Q x Q-matrix A has to be set up and inverted. Its condition number and thus its invertability depends on the number of support points and their spatial arrangement. Practical experience has revealed that the regularisation of the linear systems of equations (13) by left multiplication of [m(Xn)] is highly detrimental to its condition number. A more accurate and robust numerical solution can be achieved if instead for each surface point the Ng overdetermined systems of equations
Ф(^, Xn) [m(Xn)]T [a*(Xn)] = Ф(^, Xn) (15)
are solved with QR decomposition, yielding Ng tuples of polynomial coefficients a*(Xn) for unit deflections u*x(Xn) at the individual support points. The final row entry to the projection matrix then is
P(x) = mT (X)[a*(xn)j. (16)
Because the interpolation function (11) has only local support, the projection matrix is sparse, greatly reducing memory requirements in comparison with the GSB method.
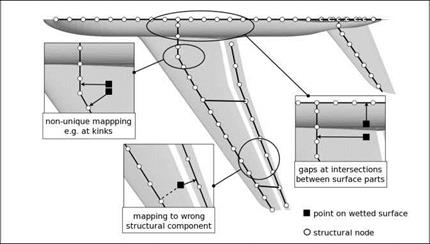
Investigations using configurations with multiple components revealed that even with these new projection methods explicitly based on interpolation schemes additional interpolation in intersection regions between assemblies cannot be avoided. If the whole configuration is treated as a single assembly during the projection, the resulting deformed wetted surface is contiguous, but extremely distorted. (With the GSB method, its global polynomial term in the interpolation function can even result in an unfeasible propagation of deformations to assemblies not directly connected, e. g. from the main wing to the empennage.)
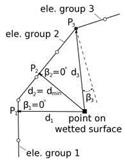
For the MLS scheme, an additional interpolation in intersection regions has been implemented that works in a similar fashion as the interpolation of the FIE method
(3) : For a surface point situated in an intersection region, as depicted on the left of Fig. 4, a row entry to the projection matrix Pk(X) is built for the element groups directly assigned. Further entries are built with the structures of each adjacent surface segment. The resulting K row entries are assigned normalised weights wk according to the surface point’s distance a to the intersection curve. Weighted averaging yields the final entry to the projection matrix for the given surface point:
KK
P(X) = £ wk(X, alimit) Pk(X) with £ wk(X, aUinit) = 1. (17)
k=1 k=1
This interpolation algorithm exploits the fact that the MLS method builds the projection matrix one surface point at a time. In the GSB method, the projection matrix is created for all points simultaneously. To realise a comparable interpolation, for each assembly a projection matrix would have to be built which relates the points of its surface segment to all neighbouring structures. Only then the average can be taken with suitable weights assigned to the row entry of each surface point. Because of the high memory requirements of just a single projection matrix resulting from the GSB method, comparable interpolation has not been implemented in the ACM.











 ucfd = X Wtot, i ucfd, i with Wtot, i
ucfd = X Wtot, i ucfd, i with Wtot, i