We do not pretend to have covered all the principles of mechanics, nor even to have explained fully those that have been covered. All we have done has been to select some aspects of the subject which seem to form the chief stumbling blocks in the understanding of how an aeroplane flies; we have attempted to remove them as stumbling blocks, and perhaps even so to arrange them that, instead, they become stepping stones to the remainder of the subject. In the next chapter we will turn to our real subject – the Mechanics of Flight.
Before continuing, try to answer some of the questions below, and the numerical questions in Appendix 3.
Can you answer these?
These questions are tests not so much of mechanical knowledge as of mechanical sense. Try to puzzle them out. Some of them are easy, some difficult; the answers are given in Appendix 5.
1 A lift is descending, and is stopping at the ground floor. In what direction is the acceleration?
2 What is the difference between –
(a) Pressure and Force?
(b) Moment and Momentum?
(c) Energy and Work?
3 Why does it require less force to pull a body up an inclined plane than lift it vertically? Is the same work done in each case?
4 Distinguish between the mass and weight of a body.
5 If the drag of an aeroplane is equal to the thrust of the propeller in straight and level flight, what makes the aeroplane go forward?
6 Is the thrust greater than the drag during take-off?
7 Can the centre of gravity of a body be outside the body itself?
8 Is an aeroplane in a state of equilibrium during –
(a) A steady climb?
(b) Take-off?
9 Are the following the same, or less, or more, on the surface of the moon as on the surface of the earth –
(a) The weight of a given body as measured on a spring balance?
(b) The apparent weight of a given body as measured on a weigh-bridge (using standard set of weights)?
(c) The time of fall of a body from 100 m?
(d) The time of swing of the same pendulum?
(e) The thrust given by a rocket?
10 In a tug-o’-war does the winning team exert more force on the rope than the losing team?
11 Are the following in equilibrium –
(a) A book resting on a table?
(b) A train ascending an incline at a steady speed?
12 A flag is flying from a vertical flag pole mounted on the top of a large balloon. If the balloon is flying in a strong but steady east wind, in what direction will the flag point?
For solutions see Appendix 5.
For numerical examples on mechanics see Appendix 3.
The moment of a force about any point is the product of the force and the perpendicular distance from the point to the line of action of the force.
Thus the moment of a force of ION about a point whose shortest distance from the line of action is 3 m (Fig. 1.11) is 10 X 3 = 30 N-m. Notice that, though both are measured by force X distance, there is a subtle but important distinction between a moment (unit N-m) and the work done by a force (unit Nm, or joules).
The distance in the moment is merely a leverage and no movement is involved; moments cannot be measured in joules.
Fig 1.11 Moment of a force (Anti-clockwise)
A moment is normally taken to be positive if it is in a clockwise direction, and negative if it is in an anti-clockwise direction.
If a body is in equilibrium under the influence of several forces in the same plane, the sum of the clockwise moments about any point is equal to the sum of the anti-clockwise moments about that point, or, what amounts to the same thing and is much shorter to express, the total moment is zero. This is called the principle of moments, and applies whether the forces are parallel or not.
When considering the forces acting on a body, the weight of the body itself is often one of the most important forces to be considered. The weight may be taken as acting through the centre of gravity, which is defined as the point through which the resultant weight acts whatever position the body may be in.
Two equal and opposite parallel forces are called a couple. The moment of a couple is one of the forces multiplied by the distance between the two, i. e. by the arm of the couple. Notice that the moment is the same about any point (Fig. 1.12), and a couple has no resultant.
Moments about O. P10Xl = 10 clock, Q10Xl = 10 clock,
Total 20 clock.
Moments about A. P zero, Q 10 X 2 = 20 clock,
Total 20 clock.
Moments about В. P 10 X 2 = 20 clock, Q zero,
Total 20 clock.
Moments about С. P 10 X 6 = 60 clock, Q 10 X 4 = 40 anti,
Total 20 clock.
P 10 newtons
Q 10 newtons
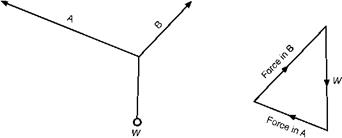
If three forces which act at a point are in equilibrium, they can be represented by the sides of a triangle taken in order (Fig. 1.10). This is called the principle of the triangle of forces, and the so-called parallelogram of forces is really the same thing, two sides and the diagonal of the parallelogram corresponding to the triangle.
If there are more than three forces, the principle of the polygon of forces is used – when any number of forces acting at a point are in equilibrium, the polygon formed by the vectors representing the forces and taken in order will form a closed figure, or, conversely, if the polygon is a closed figure the forces are in equilibrium.
A force is a vector quantity – it has magnitude and direction, and can be represented by a straight line, passing through the point at which the force is applied, its length representing the magnitude of the force, and its direction corresponding to that in which the force is acting. Forces can be added, or subtracted, to form a resultant force, or they can be resolved, that is to say, split into component parts, by drawing the vectors to represent them (Fig. 1.9).
Fig 1.9 Composition and resolution of vector quantities
Note that velocity and momentum are also vector quantities and can be represented in the same way by straight lines. Mass, on the other hand, is not; a mass has no direction, and this is yet another distinction between a force and a mass.
In the study of the flight of aircraft, we are really only interested in the behaviour of one particular gas, air. The most important relationship that we need to know is called the gas law, which can be written as:
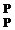 = RT = RT
where p is the pressure, p is the density, T is the temperature measured relative to absolute zero (i. e. in degrees Kelvin in the SI system), and К is a constant called the gas constant.
If the gas is compressed its density increases, so either or both the other quantities, temperature or pressure, must change. The way that they change depends on how the compression takes place. If the compression is very slow, and the gas is contained in a poorly insulated vessel so that heat is transferred out of the system, then the temperature will stay constant, and the pressure change will be directly proportional to the density change. This is called an isothermal process, and it involves a heat transfer from the gas to its surroundings. In this case the relationship between pressure and density is given by:
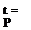 a constant a constant
If the compression takes place with no transfer of heat, which commonly occurs when compression is very rapid, then the change is said to be adiabatic. If the change also takes place without any increase in turbulence, so there is no increase in the disorder (entropy) of the system, then the process is called isentropic, and the relationship between pressure and density is given by:
P
рУ = a constant
where у is the ratio of the specific heat at constant pressure to the specific heat at constant volume, and has a value of approximately 1.4 for air.
We cannot go much further down this path without becoming embroiled in the complexities of thermodynamics, however, and as the relationships above are the only ones that are relevant to the understanding of the contents of this book, we will not pursue the subject any further.
|