Virtual Engineering
Engineers are practical people. That is the original meaning of virtual’, “being something in practice.” The Encarta World English Dictionary1 expands its meaning to “simulated by a computer for reasons of economics, convenience or performance.” We deduct that virtual engineering is computer-based engineering for the sake of increased productivity.
The computer has replaced slide rules, spirules, drawing boards, mockups, and sometimes even brassboards and breadboards. Virtual prototyping has become the Holy Grail. Engineers are challenged to design, build, and test a prototype without ever bending metal. Will we ever reach this goal of so-called simulation-based acquisition? Let the future be the judge.
Modeling and simulation are important elements of virtual engineering. They do not replace creativity, but enable the engineer to define the design and explore its performance. With our emphasis on dynamic systems, modeling means the following to us: formulating dynamic processes in mathematical language. The foundation is physics, the blocks are the vehicle components, and calculus is the mortar that joins them together. The simulation is the finished structure, programmed for computer and ready for execution.
With modeling completed and the simulation validated, we have a powerful tool to carry out these important tasks:
1) Developing performance requirements—A variety of concepts are simulated to match up technologies with requirements and to define preliminary performance specifications.
2) Guiding and validating designs—Before metal is cut, designs are tested and validated by simulation.
3) Test support—Test trajectories and footprints are precalculated, and test results are correlated with simulations.
4) Reducing test cost—A simulation, validated by flight test, is used to investigate other points in the flight envelope.
5) Investigating inaccessible environments—Simulations are the only method to check out vehicles that fly through the Martian atmosphere or land on Venus.
6) Pilot and operator training—Thousands of flight simulators help train military and civilian pilots.
7) Practicing dangerous procedures—System failures, abort procedures, and extreme flight conditions can be tried safely on simulators.
8) Gaining insight into flight dynamics—Dynamic variables can be traced through the simulation, and limiting constraints can be identified.
9) Integrating components—Understanding how subsystems interact to form a functioning vehicle.
10) Entertainment—It is fun to fly simulators.
The history of modeling and simulation spans less than a lifetime. The first flight simulator was built by Link in the 1930s. It was a mechanical device with a simple cockpit, tilting with the pilot’s stick input. The instructor used it to teach the fledgling student the three aircraft attitude motions: yawing, pitching, and rolling. When the first analog computers were introduced in the early 1960s, the linearized equations of motion of an aircraft could be solved electronically. I used a British-built Solartron computer while working on my Master’s thesis on “Stability Augmentation of Helicopters” at the Helicopter Institute in Germany.
|
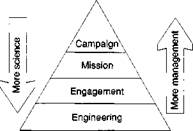
Fig. 1.1 Hierarchy of modeling and simulation. |
During that time, the first digital computers came on line, but were still incapable of solving differential equations. In the 1970s analog computers were combined with digital computers. These hybrid computers were able to simulate the nonlinear vehicle motions and any other subsystem of interest. The high-frequency motions, like body-bending, rate, and acceleration control loops, were calculated by the analog circuitry, whereas the nonlinear equations of motion were solved by the digital components. Hybrid computers dominated the simulation industry for two decades. Today, advances in digital computing have made hybrid computers obsolete.
The ever-increasing computer power is harnessed at all levels of design, testing, and management. A hierarchy of modeling and simulation (M&S) has congealed at four distinctive levels of activities: engineering, engagement, mission, and campaign (see Fig. 1.1). Though the names have military connotations, they also apply to civilian enterprises. A good exposition can be found in the book Applied Modeling and Simulation} I will just give a brief description of the four levels.
Engineering M&S provides the tools for design tradeoff at the subsystem and system level. It supports the development of design specifications, as well as test and performance evaluations. Physical laws shape the models. For instance, Newton’s and Euler’s laws generate the equations of motions, the radar range equation establishes the acquisition range, and the Navier-Stokes equation predicts aerodynamic forces. Engineering M&S establishes measures of performance for subsystem and systems. The majority of this book is devoted to its advancement.
Engagement M&S determines the effectiveness of systems. As they interact, reliability, survivability, vulnerability, and lethality are established. The scenarios are limited to one-on-one or few-on-few entities. For example, air combat simulators provide military measures of effectiveness, and air traffic simulators establish optimal approach patterns at airports. Engagement M&S is based on engineering M&S, but sacrifices fidelity to accommodate complexity. Chapter 11 covers flight simulators and in particular missile implementations in combat simulators.
Mission M&S investigates how operational goals are achieved. It broadens the scope to a greater number of players, both cooperative and adversarial. Some examples are the following: How can an airline beat the competition on the transatlantic route, or how can a carrier battle group defuse the tensions in the Persian Gulf? As various scenarios play out, measures of operational effectiveness are used to determine the best course of action.
Campaign M&S engages decision makers in broad-scale conflicts. Battle commanders practice winning strategies, and chief executive officers (CEOs) prepare for the next company takeover. Fidelity of individual models gives way to the emphasis on interplay amongst the myriad of elements, occupying large playing fields. With the emphasis on the outcome of the conflict, measures of outcome are derived to help congeal the best strategies. The ultimate campaign M&S is the war game. In Chapter 11 you have the opportunity to sample the art of wargaming.
The foundation of M&S is the engineering simulation, which establishes the performance of individual systems, based on scientific principles. As we climb the pyramid, the interplay of systems becomes more important. Synergism, tactics, and strategy exploit their performance for success. Scientific models yield to management principles, inert objects to human decision making.
With M&S penetrating so many technical and managerial disciplines, the paramount question becomes, can we trust the results. Is the simulation verified, validated, and accredited? Was the simulation built correctly according to specifications, was the right simulation built to do the job, and is it the rightfully accepted simulation for the study. These requirements are difficult to satisfy and often the time tried-and-true model wins by default.
Instead of roaming the esoteric heights of military campaigns, we will spend most of our time building the foundation of engineering models and simulations. Scientific principles will guide our venture, and high fidelity will characterize our simulations. M&S methods are like designing a model airplane, then building and flying it. You draw up specifications, lay out schematics, build the structure, and exercise the finished product.
M&S are demanding activities. Theoretical proficiency is paired with practical engineering skills. Because we are dealing with aerospace vehicles, I lay a solid foundation of flight dynamics, not shying away from some difficult modeling tasks. Chapters 2-7 are devoted to it under the umbrella of Part 1, Modeling of Flight Dynamics. Part 2, Simulation of Aerospace Vehicles, combines the dynamic equations with other engineering disciplines like aerodynamics, guidance, and control to fashion the simulations. Eight sample simulations should challenge you along the way.
As a virtual engineer you embrace the theoretical, practical, and programming challenges of M&S. Whether you are a novice or a seasoned veteran, I hope you will benefit from the following chapters. They are written to deepen your understanding of modeling of flight dynamics and to induce you to build sophisticated simulations of aerospace vehicles.
Imagine engineers without computers! It is true the great aeronautical discoveries were made without millions of transistors in pursuit of an optimal design. Heinkel used beer coasters to sketch out his famous airplanes. However, without digital computers solving the navigation equations, Neil Armstrong would not have set foot on the moon. It was in that decade, the 1960s, that I replaced my slide rule first by analog and then by digital computers. Certainly, I have no desire to return to the “good old days.”
With the blessing of computers came also the curse to feed the beasts. They are insatiable, devouring innumerable lines of code. Who feeds them? Engineers do. Today, we design a big airplane like the Boeing 777 without a scrap of paper. Yes, we develop and use computer tools lavishly, but also try to keep our identity as visionaries of air and space travel.
In the following chapters I help you to model and simulate your visions. We presume that the design already exists and is defined by its subsystems, like aerodynamics, propulsion, guidance and control. You will leam how to formulate the dynamic behavior of your vehicle in a concise mathematical form and how to convert this model into computer code. You will write your own simulations in CADAC, a PC-based set of dynamic modeling tools. With its graphic charts you can promote your design among your peers.
We will use tensors to model vehicle dynamics, independent of coordinate systems. The simplest form of Cartesian tensors will suffice. They will serve us better than the vector formulation of so-called vector mechanics. The tensor’s invariance under time-dependent coordinate transformations is a crucial characteristic in a dynamic environment that features a plethora of coordinate systems.
For programming we convert the tensor model into matrices by introducing suitable coordinate systems. Modem computers love to chew on matrices. Even the latest version of the venerable FORTRAN language features intrinsic matrix functions and instructions for parallel processing. So let us abandon the old habit of scalar coding and replace it by compact matrix expressions.
The poor man does flight testing on computers. Call it virtual testing, testing in cyberspace, or just plain computer runs. Instead of hardware, you build simulations and fly them without the whole world witnessing your new creation hitting the dirt.
Come join me in this adventure of modeling and simulation of aerospace vehicles. The ride will not be easy. There are some mathematical hairpins in the road we have to negotiate together. Once at the top, you can simulate all of the visions before you and only the sky will be the limit. Yet, what is even more important, you will have become a better engineer.
The time has come to give an account of modeling and simulation to aerospace students and professionals. What has languished in notebooks, papers, and reports should be made available to a wider audience. With modeling and simulation (M&S) penetrating technical disciplines at every level, engineers must understand its role and be able to exploit its strength. If you aspire to acquire a working knowledge of modeling and simulation of aerospace vehicle dynamics, this book is for you. It approaches modeling of flight dynamics in a novel way. covers many types of aerospace vehicles, and gives you hands-on experience with simulations.
The genesis of this text goes back to the years when the term M&S was still unknown. The challenges then were as great as today. Every new generation of computers was pressed into service as soon as it came on line. With analog computers, we could solve linear differential equations. Later, digital computers empowered us to master also nonlinear differential equations. Concurrently, flight dynamics evolved from Etkin’s linearized equations to today’s dominance of nonlinear equations of motion.
As computers became more powerful, the tasks grew more complex. The fidelity of models increased, the number of vehicles multiplied, and coordinate systems abounded. In the late 1960s, as I worked on my dissertation, it became clear that these complex models called for compact computer coding. Matrices are the conduit, and tensors are the theoretical underpinning. Thus evolved the invariant modeling of flight dynamics, my contribution to M&S.
In the late 1970s, I began to teach this approach at the University of Florida. What was first called “Advanced Flight Mechanics I and II” became in the 1990s “Modeling and Simulation of Aerospace Vehicles.” In the meantime, as I worked for the U. S. Army and Air Force, I had the opportunity to apply these techniques to rockets, missiles, aircraft, and spacecraft.
Thus matured the two tracks of this book: invariant modeling of flight dynamics and computer simulations of aerospace vehicles—theory and praxis. The first part lays out the mathematical foundation of modeling with Cartesian tensors, matrices, and coordinate systems. Replacing the ordinary time derivative with the rotational time derivative and using the Euler transformation of frames enables the formulation of the equations of motions in tensor form, invariant under time-dependent coordinate transformations. Newton’s law yields the translational equations, and Euler’s law produces the attitude equations. Perturbation equations and aerodynamic derivatives complete the modeling of flight dynamics.
The second part applies these concepts to aerospace vehicles. Simple three- degrees-of-freedom (three-DoF) trajectory simulations are built for hypersonic aircraft, rockets, and single-stage-to-orbit vehicles. Adding two attitude degrees of freedom forms the five-degrees-of-freedom (five-DoF) simulations. Cruise
During the six years of publication this book has made many friends. Some enjoyed the theoretical Part 1 of tensor flight dynamics, others jump-started their aerospace simulations with Part 2. Though I aimed to produce a perfect product, some mistakes lingered until detected either by readers or by my own scrutiny.
However, this second edition is more than just an updated reprint. It contains two new appendices. The original Appendix C, which reviewed state-of-the-art FORTRAN simulations, has been replaced by the description of three self-study CD-ROMs of aerospace simulations in C++. These CDs broaden the applications of this book by spanning from simple three-degrees-of-freedom cruise missiles to high fidelity missiles, aircraft, and hypersonic vehicles. The new Appendix D lays the theoretical foundation of tensor flight dynamics. It contains the proofs of the rotational time derivative and the Euler transformation, which the main text alludes to. Furthermore, Examples 4.4 and 5.6 have been rewritten, and Problem
7.1 was added.
Many examples in the book refer to the CADAC FORTRAN code, which is provided on the CADAC CD-ROM that also contains plotting programs. To qualify for a complimentary CD, see the instructions on the Supporting Materials page at the back of this book.
I am grateful for the feedback I received from around the world. Significant contributions were made by Gary Allen, Philippe Guicheteau, Don Koks, Mark Smith, and Martin Weiss. Most of their suggestions have been implemented. I also want to thank the AIAA publications staff, and in particular Rodger Williams, who has steered my authorship with a steady hand through a few tempests.
Above all I thank you, the reader, for giving me the honor to be your companion on your professional journey through the world of aerospace vehicle modeling and simulation. May our voyage be a pleasant one!
Peter H. Zipfel
November 2006