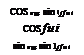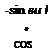As you may have suspected all along, Earth is flat, at least for many engineers who develop simulations for aircraft and short-range missiles. They make Earth
the inertial frame and unwrap the curved longitude and latitude grid into a local plane tangential to Earth near liftoff. What a helpful assumption! It eliminates several coordinate transformations, simplifies the calculation of the body rates, and eliminates the distinction between inertial and geographic velocity.
If in Chapter 5, Eq. (5.25), the terms of Coriolis and transport acceleration are neglected, we obtain a form of Newton’s second law that assumes the Earth frame E is the inertial frame. We replace in Eq. (9.4) the inertial reference frame / by E and reinterpret the inertial velocity frame U as the geographic velocity frame V. The Hat-Earth equations of motions are then
[Dvveb][2] + [fiv£]v[uf]v = ^([fa, Plv + [ЛИ (9.20)
with [vf ]v = [V 0 0], the geographic velocity of the c. m. wrt Earth expressed in geographic velocity coordinates, and [S1VEY the skew-symmetric equivalent of the angular velocity [ojve]v of the geographic velocity frame wrt Earth. The rotational time derivative is simply
On the right-hand side of (9.20), we must convert [fa, P]v = [f]BV[fa, p]B because the aeropropulsive forces are usually given in body coordinates. The gravity force is expressed best in local geographic coordinates, which for the round-Earth case were designated by ]G. With the flat-Earth assumption they are renamed local – level coordinates with the label ]L. Finally, we calculate the gravity force from [fg]v — [T]VL[fg]L with [fg]L = mB[0 0 g] and g the gravity acceleration.
Before Eq. (9.20) can be programmed, we have to convert the kinematic relationships to the flat-Earth case. We need the transformations [T]BV, T]VL, and [T]BL the angular velocity vectors [<yV£]> [caBV], and [шВЕ].
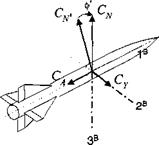
The transformation matrix [ T ]VL of the velocity wrt the local-level coordinates derives directly from Eq. (9.5). Just replace the angles фщ, вщ by the geographic heading angle фУь and flight-path angle 6Vi both referenced to the local-level coordinate axes. Alas, we are back on familiar ground. The obscure фщ, вщ angles have become the tried and true heading and flight-path angles on the Earth, which we called in Chapter 3 x and у, but prefer to designate here фг and Bvl – Figure 9.1 still applies with these changes, and Eq. (9.5) becomes cos 6VL cos фуі cos 6Vl sin фур — sin
![Equations of Motion over Flat Earth Подпись: [T]VL —](/img/3132/image717.gif)
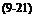 — sini/fyi COS фуі 0
— sini/fyi COS фуі 0
sin 6Vi cos фуь sin Bvl sin фуі cos Bvi
The incidence angle transformation matrix [T]vv is retained for both the skid-to – turn and bank-to-turn vehicles. They are given by Eqs. (9.8) and (9.11), respectively. The direction cosine matrix [T]BL of body wrt local-level coordinates is the composition of
|
Now we convert the angular velocity vectors to the Hat-Earth case. The angular velocity coVEv of the velocity frame wrt the Earth frame and expressed in the velocity coordinates is obtained from Eq. (9.7) by redefining the inertial frame I to become the Earth frame E and the angles фщ, Ощ to change to фуь, 6yB:
|
|
|
-фуі smeVL
6vL
tvL COS 0VL
|
|
|
|
|
|
|
The incidence angular rates are transcribed from Eq. (9.10) for skid-to-tum missiles
|
|
|
|
|
|
|
|
and for bank-to-tum aircraft from Eq. (9.13)
|
|
|
|
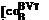 |
|
|

фВу is the bank angle of the normal load factor plane rotated about the [vB ] vector from the vertical plane. Finally, the body rates [coBE] are the vectorial addition
in body axes
[wBE]B = [coBV]B + [T]bv[cove]v (9.26)
Notice how much simpler the calculation of the body rates is with the Hat-Earth assumption than for the round rotating Earth, Eq. (9.17). The simplification occurred because geographic and inertial velocities are undistinguishable. The kinematic conversions are now complete!
For programming, the left-hand side of the dynamic equations, Eq. (9.20), must be expressed in component form. We go back to the round-Earth component equations, Eq. (9.19), and modify them for the Hat-Earth case:
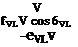 = [T]BV-^[fa, Pf + YT]VL^-[fg]L (9.27)
= [T]BV-^[fa, Pf + YT]VL^-[fg]L (9.27)
mB mB V
Let us expand the right-hand side of Eq. (9.27). The aerodynamic and propulsive term can be expressed in velocity coordinates directly. Lift and drag are referred to these coordinates, and thrust, usually parallel to the 1й axis, is projected by the angle of attack into the 1v axis. With these conventions we can adopt the three – DoF aerodynamic model of Sec. 8.2.3 to five-DoF simulations. From Fig. 8.14, A3 Forces, we borrow the formulation of the specific force:
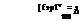 F cosa — qSCp
F cosa — qSCp
sin<t>Bv{F sina + qSCi)
—cos фву(Р sin a: +qSCL)
where F is the thrust, q the dynamic pressure, and S the aerodynamic reference area. In five-DoF simulations the lift and drag coefficients may now be more complicated functions of Mach and a than the simple parabolic flight polars of Chapter 8. More will be said about this subject in Sec. 9.2.1.
The gravity term of Eq. (9.27) is multiplied by the transformation matrix of Eq. (9.21). Combining the right-hand components with the left-hand side of Eq. (9.27) yields
|
V
|
1
III ^
|
F cosa — qSCo
|
|
-sin вуї
|
|
fVLV cos eVL
|
sin фву (F sina + qSCb)
|
+ g
|
0
|
|
1
1
s
1
|
|
—cos sina + qSCL)
|
|
COS вуї
|
(9.28)
Before you program these equations, clear the left-hand side of anything but the state variable derivatives V, ф v/ , and вуї,. You have three first-order differential equations with angle of attack a and bank angle фву as input. How this input is generated is the subject of the following sections.
![]() Ca — —Ci sina + Co cosa Сц = Ci cos a + Co sin a
Ca — —Ci sina + Co cosa Сц = Ci cos a + Co sin a![]() Cx = Ci sina — Co cos a
Cx = Ci sina — Co cos a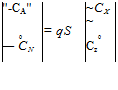
![]() (9.35)
(9.35)










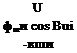 = lT]BU^[fa, P]B + [T]UG^[fgf (9.19) ma ma
= lT]BU^[fa, P]B + [T]UG^[fgf (9.19) ma ma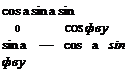
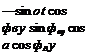
![Coordinate Transformation Matrices and Angular Rates Подпись: Fig. 9.1 [T]GI transformation.](/img/3132/image690.gif)