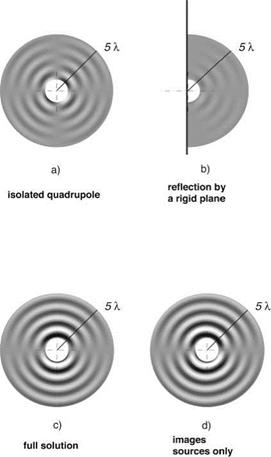
General Solution
For the sake of generality, assume a prescribed source distribution S(y, t’) radiating in a volume of space V (t’) limited by possibly moving surfaces S(t’). The local normal on the surfaces n is pointing outwards the volume. The wave equation for the scalar field variable v to be solved is written as
![]() S.
S.
Is called a Green’s function for this equation and noted G any solution in the case of an impulse point source, according to
where S is Dirac’s delta function. G depends on four variables and represents the field produced at point x and time t by an elementary source at point y and time t’. If the effect of initial conditions is ignored, which is justified for periodic or stationary random processes, the formal solution for the scalar field follows as (Goldstein (1976))
The Green’s function is not unique as long as no boundary condition is involved in its definition, but its expression must be known in order that explicit solutions are derived. The so-called tailored Green’s function would provide the field produced at point x and time t by an elementary source at point y and time t’ in the presence of the surfaces. If it can be known and introduced in the solution, then the surface integral vanishes. The corresponding explicit result generally leads to closed-form solutions. If another Green’s function is used, the result is implicit and the formal solution is an integral equation. The simplest statement is obtained with the free-space Green’s function Go for which the volume integral represents the direct field radiated by the source distribution and the surface integral represents all
effects of reflection and diffraction by the surfaces. The surface integral of course vanishes for sources radiating in free space, since no boundaries are present. This is assumed in the next and leads to the simplest solving procedure. Within the scope of the acoustic analogy, this formal simplicity is a great advantage of Ffowcs Williams & Hawkings’ equation, obtained by considering the solid surfaces not as boundary conditions but rather as equivalent sources. The general free-field solution reads
and the free-space Green’s function has the fairly simple expression
![]() S(t’ —1 + R/co)
S(t’ —1 + R/co)
4 n R
with R = |R| = |x — y|. Reduction of the time integral by the property of the delta-function leads to the formula of retarded potentials
The quantity te = t — R/c0 is the retarded time or the emission time of the source at point y, corresponding to a contribution at point x and time t. Conventionally, the evaluation of a quantity at the retarded time is denoted by squared brackets. The integral is to be performed over the actual, finite extent of the source distribution.
It is worth noting that for monochromatic fields of time dependence e—iut, the wave equation reduces to the Helmholtz equation, written below for the corresponding Green’s function as
{Д + k2} Gu = — S(x — y),
with k = ш/co. The solution reads
![]() R/co
R/co
4 n R
It is seen that Go et Gu eiut are conjugate quantities by Fourier transform.