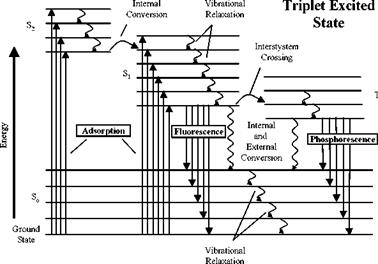
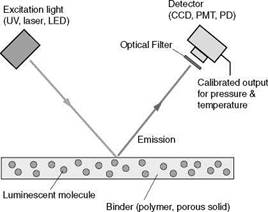
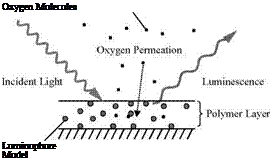
From a standpoint of engineering application, it is unnecessary to analyze all the intermediate photophysical processes and their interactions. Therefore, a lumped model for luminescence (fluorescence and phosphorescence) is given here by considering the main processes: excitation, luminescent radiation, non-radiative deactivation, and quenching. The luminophore is excited by a photon from a ground state L0 to an excited state L, i. e., L0 + hv — L. The excited state L returns to the ground state L0 by either a radiative process (emission) or a radiationless process (deactivation). In the radiative process, the luminescent
* k
emission releases energy of hv,, that is L*——- -——L0 + hv,, where kr is the rate
constant for the radiation process and v, is the frequency of the luminescent emission. In the deactivation process, L* returns to L0 by releasing heat, which
* к
is expressed as L —— -—— L0 + A, where knr is the rate constant for the combined
effect of all the non-radiative processes. If temperature around a luminophore molecule increases, the deactivation rate increases, reducing the radiative process from L*. Thus, the rate constant knr for the non-radiative processes is
temperature-dependent. The quenching process by a quencher Q is expressed as к
L* + Q——- —>L0 + Q*, where kq is the rate constant of the quenching process
and Q* denotes the excited quencher. The molecular oxygen O2 in the ground state is an efficient quencher for both the excited singlet and triplet states. The molecular oxygen is excited to O* once it quenches luminescence, i. e., L + O2 ^ L0 + O*. By combining the rates of emission, deactivation and quenching processes, the rate of change of the population of the excited state [L* ] is given by the first-order equation
= I a – (kr + knr + kq[Q])[L*] . (2.3)
dt
The rate of excitation is Ia = ks1[L0], where [L0] is the population in the ground state and ks1 is the rate constant for excitation. At a steady state d[L* ] / dt = 0, without quenching ([Q] = 0 ), we have
I a = {kr + knr )[L*] . (2.4)
The amount of luminophore molecules in a given excited state is described by the quantum yield of luminescence defined by
^ rate of luminescence
Ф =—————————— . (2.5)
rate of excitation
The quantum yield Ф for the luminescent emission from L* with the quencher Q is expressed by
ф= kr[L ] =————— hr——— = J_, (2.6)
Ia kr + knr + kq[Q] Ia
where I is the luminescent intensity. The quantum yield without quenching is
where I0 is the luminescent intensity without quenching. Dividing Ф0 by Ф , we obtain the well-known Stern-Volmer relation
where T0 = 1/(kr + k^) is the luminescent lifetime without quenching. The luminescent lifetime with the quencher is
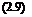 1
1
T =———————–
kr + knr + kq[ Q]
Thus, Eq. (2.8) can be written as
ф0/ Ф = т0/т. (2.10)
When the quencher is oxygen, the Stern-Volmer equation is
I т
-f =-0- = 1 + kqT0[O2]. (2.11)
I т
In general, the rate constants knr and kq for the non-radiative and quenching processes are temperature-dependent. The temperature dependency of knr can be decomposed into a temperature-independent term and a temperature-dependent term modeled by the Arrhenius relation (Bennett and McCartin 1966; Song and Fayer 1991), i. e.,
E
knr = knro + knriexp(—£~) , (2.12)
where krr0 = knr(T = 0) and knr1 are the rate constants for the temperature – independent and temperature-dependent processes, respectively, Enr is the activation energy for the non-radiative process, R is the universal gas constant, and T is the absolute temperature in Kelvin. The temperature dependency of the rate constant kq for the quenching process is related to oxygen diffusion in a
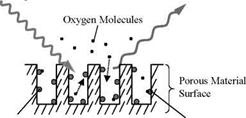
homogenous polymer layer used for a conventional PSP. According to the Smoluchowski relation, the rate constant kq for the oxygen quenching can be
described by
kq = 4nRABN0D (2.13)
where Rab is an interaction distance between the luminophore and oxygen molecules, and N0 is the Avogadro’s number. The diffusivity D has the temperature dependency modeled by the Arrhenius relation
E
D = D0 exp(—– —) , (2.14)
where ED is the activation energy for the oxygen diffusion process. Therefore, from Eq. (2.9), the reciprocal of the luminescent lifetime is
According to Henry’s law, the oxygen population [O2]polymer in a polymer binder is proportional to the partial pressure of oxygen pO or air pressure p, i. e.,
[ O 2] polymer = spo2 = s0o2p (2.16)
where S is the oxygen solubility in a polymer binder layer and ф02 is the mole fraction of oxygen in the testing gas. The mole fraction of oxygen ф02 is 21% in the atmosphere, but it varies depending on testing facilities. For example, ф0і is only a few ppm (1ppm = 10-4%) in a cryogenic wind tunnel where the working gas is nitrogen. Defining the permeability P0 = SD0, from Eq. (2.15), we have
– = ka + Kp, (2.17)
T
where the coefficients ka and K are defined as
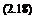
 E E
E E
ka = kr + knro + k„riexp(–E-) and K = 4nRABNoPoexp(–^)фо Rl Rl
In aerodynamic applications, it is difficult to obtain the zero-oxygen condition since the working gas in most wind tunnels is air containing 21% oxygen. Thus, instead of using the zero-oxygen condition, we usually utilize the zero-speed (wind-off) condition as a reference. Taking a luminescent intensity ratio between the wind-off and wind-on conditions, we obtain the Stern-Volmer equation suitable to aerodynamic applications
The Stern-Volmer coefficients in Eq. (2.19) are
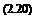 ka K
ka K
Apolymer Apolymer, ref, and Bpolymer Bpolymer, ref
karef Kref
where the reference coefficients are defined as
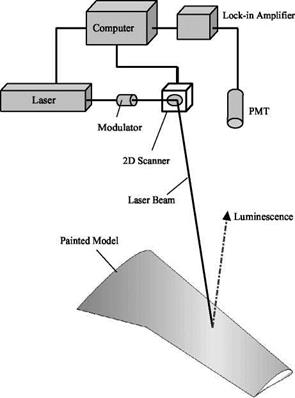
The subscript ‘polymer’ specifically denotes a conventional polymer-based PSP; it will be seen that porous PSPs have somewhat different forms of the Stern- Volmer coefficients. Eq. (2.19) indicates that a ratio between the luminescent intensities in the wind-on and wind-off conditions is required to determine air pressure. This intensity-ratio method is commonly employed in PSP and TSP measurements.
Using the expressions for ka and K, we can write Apolymer and Bpolymer as a
function of temperature
Apolymer Apolymer ,ref
1 + £exp( – Enr/RT) [1]
 |
|
|
|
|
|
B polymer B polymer, ref exp
|
|
|
|

where the factor £ is defined as £ = knr1 /(kr + knr0) . For (T – Tref ) / Tref << 1, the linearized expressions for Apolymer and Bpolymer are
where the factor n is
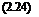 £eXp(- E„rlRTref)
£eXp(- E„rlRTref)
n =—————— – —- – —
1 + £ exp( – Enr/RTref)
Clearly, the Stern-Volmer coefficients Apolymer and Bpolymer satisfy the following
constraint
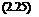 Apolymer (Tref ) + Bpolymer (Tref ) 1 ‘
Apolymer (Tref ) + Bpolymer (Tref ) 1 ‘
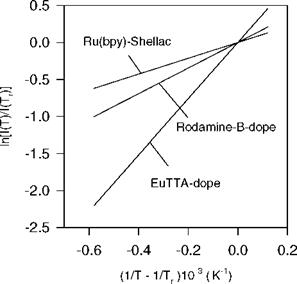
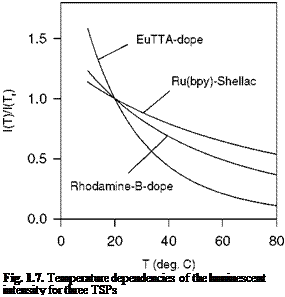
Eq. (2.23) indicates that the Stern-Volmer coefficient B polymer depends on the activity energy ED for the oxygen diffusion process; this implies that the temperature sensitivity of PSP is mainly related to the oxygen diffusion. Indeed, experiments conducted by Gewehr and Delpy (1993) and Schanze et al. (1997) for two different oxygen sensors showed that the temperature dependency of the oxygen diffusivity in a polymer dominated the temperature effect of PSP. This finding has an important implication in the design of low-temperature-sensitive PSP formulations; the low-temperature-sensitive PSP should have a polymer binder with the low activation energy for oxygen diffusion. In another special case where ED ~ Enr and n ~ 1 over a certain range of temperature, the coefficients Apoiymer(T) and Bpolymer(T) have the same temperature dependency; thus a ratio between Apolymer(T) and Bpolymer(T) becomes temperature
independent. PSP satisfying the above conditions is so-called ‘ideal’ PSP (see Section 3.6). This paint is advantageous for correcting the temperature effect since the Stern-Volmer relation becomes temperature independent when the intensity ratio scaled by a single temperature-dependent factor is used as a similarity variable.
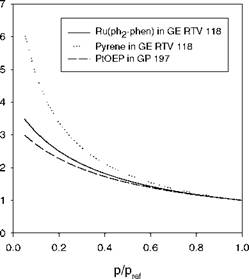
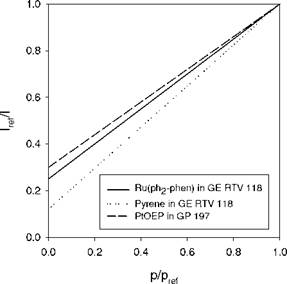
In many PSP measurements, the linear Stern-Volmer relation Eq. (2.19) is sufficiently accurate in a certain range of pressure. However, over an extended range of the partial pressure of oxygen or air pressure, the non-linear Stern-
Volmer behavior becomes appreciable for microheterogeneous PSPs (Carraway et al. 1991a; Xu et al. 1994; Hartmann et al. 1995). The main physical mechanisms behind the non-linear Stern-Volmer characteristics are associated with microheterogeneity of the environment of a probe molecule and deviation from Henry’s law. Solid-state matrices like polymers may provide numerous different kinds of environments for a probe molecule, resulting in the non-exponential decay or multiple-exponential decay of luminescence. In some cases, a double exponential model is sufficient for the decay; thus the oxygen quenching of luminescence in microheterogeneous systems is described by a two-component model
where f01 and f02 are the fractional intensity contributions of the two
components in the absence of oxygen (f01 + f02 = 1), KSV1 and KSV2 are the
where C is the Langmuir gas capacity due to adsorption and b is the Langumir affinity coefficient. Based on the dual sorption model Eq. (2.27), Hubner and Carroll (1997) suggested an extended form of the Stern-Volmer relation
Eq. (2.28) was able to give a good fit to experimental data for some PSPs. From a standpoint of aerodynamic applications, an empirical form of the non-linear Stern – Volmer relation is usually given by a polynomial
![]() 1 Geff No Фо2
1 Geff No Фо2![]() where the coefficients at the reference conditions are defined as
where the coefficients at the reference conditions are defined as










 (a)
(a)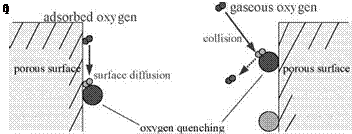
 E E
E E