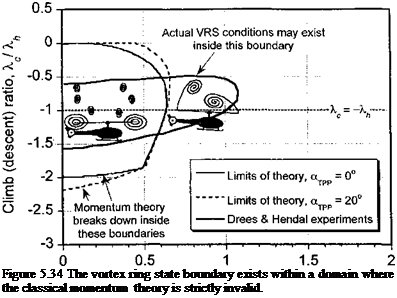
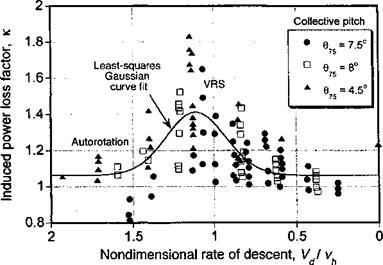
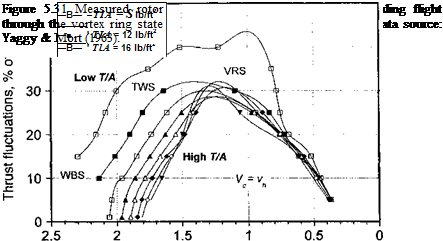
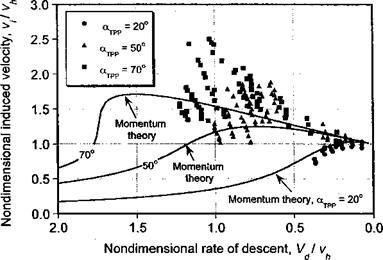
The analysis of the transient (nonsteady) maneuver of a helicopter can be approached using energy methods – see Schillings et al. (1990), Lappos (1984), and Ebert & Lappos (1985). The instantaneous energy state of the helicopter, E, can be written as a sum of its potential energy, translational kinetic energy and the rotational kinetic energy stored in the rotor, that is,
1/W і 1 9
E = wh + – l-jvl + – IRn (5.109)

where W is the weight of the aircraft, h is its altitude relative to a datum (normally the ground), Vqo is true airspeed, IR is the rotor inertia, and Q is the rotational speed of the rotor. The time rate of transfer of energy between these three different energy states of the helicopter is equivalent to the power required to change the energy level. This transfer of excess power provides a measure of maneuver capability and the rate of transfer of power is a measure of its potential agility (i. e., the quickness of the maneuver). By differentiating Eq. 5.109 with respect to time this gives
The net excess power available can be written as a contribution from the engine(s) and from the rate of change of energy level associated with changes in the flight condition, that is, the net excess power available is
AP — APengine + A Penergy level) (5.111)
where A P can be viewed as the net excess power available over and above that required for equilibrium flight at any one flight condition (i. e., at any given altitude, airspeed, rotor rpm and maneuver state). For example, any excess power available can be used to increase potential energy (gain more altitude), to increase kinetic energy (gain more airspeed), to increase the rotor energy (increase rotor rpm) or otherwise change the flight condition. The signs and magnitude of the various energy rates define the nature of the changes that are possible to the flight condition of the helicopter. For most normal flight conditions the rotor rpm is automatically governed to allow only small variations, but an overspeed (but not much of an underspeed) of the rotor can be allowed under some conditions.
The energy to produce extra rotor thrust to perform an accelerated maneuver comes from either excess shaft power available or from the conversion of one energy state to another. Rotor overspeeds can also be used for this purpose (T cx f22), but rarely is this done in practice because of the risk of overstressing the rotor. Rotor overspeeds, however, are often used during the final transient stages of an emergency autorotative maneuver, where the pilot will flare the helicopter to a steep nose-high attitude to gain excess rotor rpm to aid in a safe touchdown – see page 248.
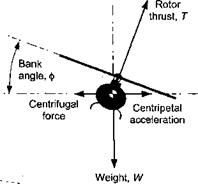
For a conventional helicopter the rotor thrust T can be estimated from the product of the gross weight of the aircraft W and the rotor load factor n. Consider a helicopter undergoing a simple pull-up maneuver, as shown in Fig. 5.40(a). The normal acceleration, a, is
a = (n – l)g =z + qVOQ. (5.112)
The potential load factor also depends partly on the ability to produce a normal (vertical) acceleration z through the application of blade pitch. The helicopter must have, therefore, an excess power available at the rotor shaft over and above that required for level, unaccelerated flight at the same conditions (i. e., at the same airspeed, weight, and density altitude). Notice that the potential load factor also depends on the energy level through the flight velocity and the ability to actually produce a pitch rate q through the application of flight control inputs.
The excess power available A P over and above that power required P at a given airspeed Too is available to produce extra rotor thrust AT and, therefore, to produce an acceleration. In horizontal flight (or conditions that may be nearly so) the equation of motion is
The load factor on the helicopter is then
(5.114)
The ability to produce this load factor depends on the stall margin of the rotor, which in this case can be defined in terms of the value of Cj I о that will produce stall relative to the lg level flight value, that is,
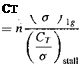 (5.115)
(5.115)
IfATsm > 1 then the rotor stall boundary will be exceeded before the power limit is reached. Therefore, an excess power available is no guarantee of maneuver capability, and both power and rotor stall margins must be addressed.
The load factors possible with a conventional helicopter are shown in Fig. 5.41, where a helicopter was flown in various transient maneuvers such as decelerating pull-ups and turns at different airspeeds in an attempt to define its transient maneuver envelope – see Lappos & Padfield (1994). The demonstrated (flight-tested) load factors are limited at low airspeeds by the low translational kinetic energy and by the relatively low excess power margin of the conventional helicopter. This type of comparison can, for now, be considered only qualitative in nature but it serves to illustrate how the shape of the measured maneuver envelope at low flight speeds mimics the excess engine power available (power margin) curve – see discussion in Section 5.5.4. It is reasonable to assume that this behavior is typical of any conventional helicopter (i. e., one without benefits of lift or thrust compounding).
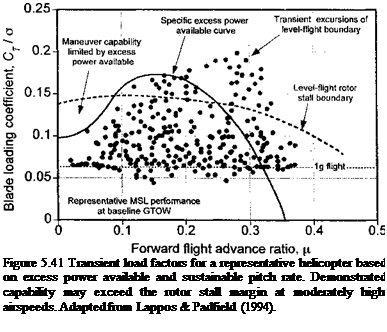 |
At intermediate forward flight speeds the transient maneuver capability is less dependent on the excess engine power available because the power margin is greater as rotor induced losses are lower, and also because the higher translational kinetic energy of the helicopter

allows for a transfer of energy (see Eq. 5.110). Flight test results indicate that in some cases these transient load factors may be of the order of 3g and are likely to well-exceed the normal static stall boundary of the rotor and approach its structural limits. Some part of these overshoots in the static stall envelope can be attributed to the delay in the onset of stall that is associated with the favorable effects of pitch rate on stall – a phenomenon recognized by Brown & Schmidt (1963) and discussed in detail in Chapter 9. There are also gyroscopic effects on the rotor during maneuvers, which affects the blade flapping response (see Section 6.9.3). The corresponding changes in blade section AoA can add or subtract from the stall margins depending on the nature of the maneuver (rolls to the left or right,
The potential maneuver capability from the excess engine power available can be estimated with reference to the engine power required versus power available curves. The excess rotor power available Д Peng can be related to the potential of increasing rotor thrust, AT. In low-speed flight (i. e., near to hovering flight), it is sufficient to assume the hover result relating rotor power required to rotor thrust using the momentum theory, that is,
/ 1 7*3/2
P =———- —=, (5.116)
FM) V2^A ’
where A is the rotor disk area, FM is the rotor figure of merit, and p is the air density at the actual operational flight conditions. Differentiating the power equation with respect to thrust gives
 (5.117)
(5.117)
Linearizing the problem by assuming the excess thrust and engine power are a fraction of those required at the level, unaccelerated flight condition means the excess power can be written as
Using the result from Eq. 5.117, and assuming that the increase in thrust is relatively small compared to the thrust required for level, unaccelerated flight at that gross weight and
density altitude gives the potential load factor as

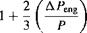 (5.122)
(5.122)
where it is assumed that all of the excess engine power available can, in fact, be used to generate an extra rotor thrust (i. e., the rotor is not stall limited before being power limited). Therefore, Eq. 5.122 confirms the hypothesis made earlier that the ability to produce a maneuver load factor on the aircraft depends on the specific excess power available. This particular result is valid at low airspeeds where the translational kinetic energy is low and where the shape of the excess power available curve closely mimics the actual maneuver capability of the helicopter.
This problem can also be examined by assuming that the power required by the rotor is approximated by the forward flight result
p = T^7T + po + Pp^ (5-123)
IpAVoo
where P0 is the profile power required and Pp is the parasitic power. The first term in Eq. 5.124 is the induced power required as given by Glauert’s approximation (Eq. 2.114). The profile and parasitic terms are primarily a function of flight speed V^. The profile term is nominally constant in low-speed flight, and the parasitic term increases only slowly when in low-speed forward speed. Therefore
By differentiation of Eq. 5.124, the approximate change in power required with respect to a change in rotor thrust can be written as
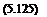 dP _ kT dT pAVoo
dP _ kT dT pAVoo
As before, linearizing the problem by assuming the excess power (and thrust) is a fraction of the power available means the excess power can be written in terms of the excess thrust. Using the result in Eq. 5.125 by assuming that the change in rotor thrust is a fraction of the thrust required at that aircraft weight, gives the potential load factor as
These results help quantify the effects of excess engine power available on the potential maneuver capability of the helicopter, which approximately mimics the curve of excess power available relative to level flight. However, it is clear that the maneuver capability depends on many interrelated parameters, including the translational kinetic energy of the helicopter, the kinematics of its flight trajectory, and the stall margins of the rotor.











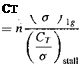 (5.115)
(5.115)

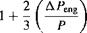 (5.122)
(5.122)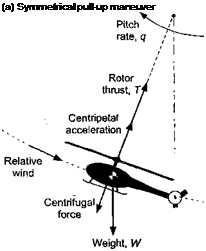

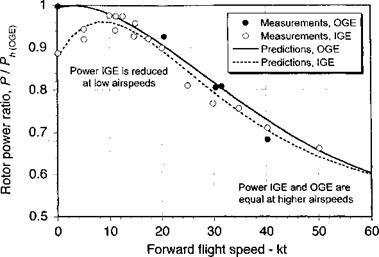
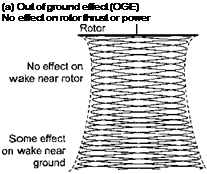
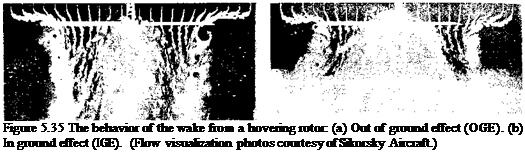
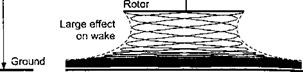
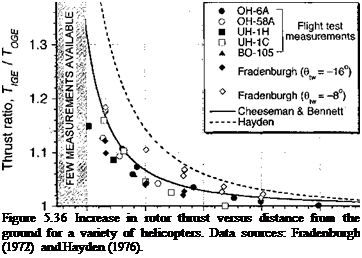 helicopters. Data sources: Fradenburgh (1972) and Hayden (1976). ” width=”362″ height=”258″/>
helicopters. Data sources: Fradenburgh (1972) and Hayden (1976). ” width=”362″ height=”258″/>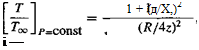
 (5.97)
(5.97)