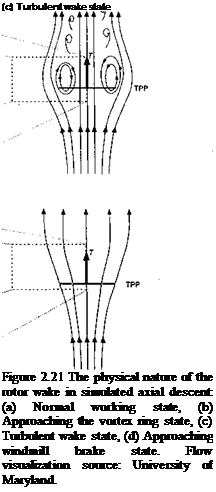
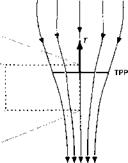
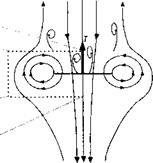
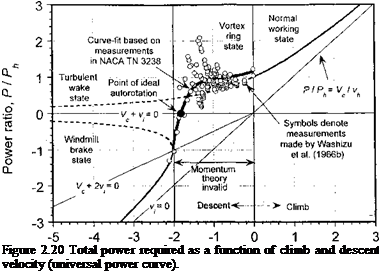
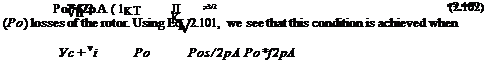Rotor Power Requirements in Forward Flight
The rotor power in forward flight is given by the equation
P = r(VooSina + Vi) = TVoosina + Tu, (2.139)
assuming no viscous losses at this stage. The first term on the right-hand side of the above equation is the power required to propel the rotor forward and also to climb. The second
term is the induced power. As for the axial flight case, we may reference the rotor power in forward flight to the hover result and so
![]() P P TfVoo sin a + VooSina + u,- X Ph T vh T vh vh Xh
P P TfVoo sin a + VooSina + u,- X Ph T vh T vh vh Xh
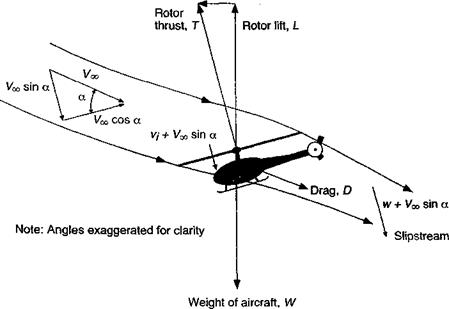
Therefore, the form of the power curve simply mimics the inflow curves shown previously in Fig. 2.26. Notice that the power requirements decrease significantly to a minimum value and then increase again. This is a fundamental characteristic of a helicopter and the behavior[12] is examined in much further detail in Chapter 5. The behavior was first noticed in early experiments by Maxim (1897), Riabouchinsky (1906), and Beliner (1908) (see page 16). The results also depend on the disk angle of attack, which must always be tilted forward slightly for propulsion (see Fig. 2.23). Recall that
Therefore,
The first term on the right-hand side of the above equation is the extra power to meet propulsion and climb requirements, whereas the second term is the induced power. As mentioned previously, the evaluation of the propulsive power requires a knowledge of the rotor disk angle of attack, which in turn requires a knowledge of the helicopter’s drag, D. Assuming straight-and-level flight, the disk angle of attack, a, can be calculated from a simple force equilibrium (see Fig. 2.23). For vertical equilibrium T cos a — W and for horizontal equilibrium T sin a = Dcosa « D. Therefore,
which is expressed in terms of the helicopter’s overall lift-to-drag ratio. Therefore, the power equation in straight-and-level flight can be written as
![]() P_ – !L (—) + kh
P_ – !L (—) + kh
Ръ xhTj Уд2 + x2
The determination of D, however, requires a knowledge of both the drag on the rotor and the drag on the airframe, the latter of which is called parasitic drag. The rotor drag must be estimated using blade element theory. The AoA of the disk relative to the oncoming flow will change in a climb or descent, thereby altering the power required. In this case, the power ratio can be written as
— = Ac cos a + — tana H—— (2.145)
Ph ^h yjpf + X2
where Xc is climb velocity ratio. In each case, the disk AoA can be solved for on the basis of a free-flight force equilibrium (even if this is only approximate).











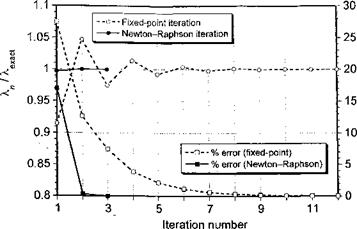

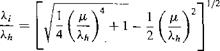 (2.130)
(2.130)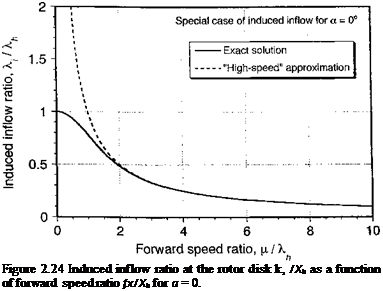
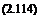 T = 2 pAviV0
T = 2 pAviV0