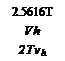The momentum theory analysis has found use in the analysis of other helicopter rotor designs, including contrarotating coaxials, tandems, and ducted fans. The former are now discussed, with the ducted fan problem being discussed later in relation to a fan-in-fin rotor or fenestron concept in Section 6.10.1.
2.15.1 Coaxial Rotor Systems
One advantage of the contrarotating coaxial rotor design is that the net size of the rotor(s) is reduced (for a given helicopter gross weight) because each rotor now provides vertical thrust. In addition, no tail rotor is required for anti-torque purposes, so that all power can be devoted to providing useful vertical lift and performance. However, the two rotors and their wakes interact with one another (e. g., Fig 1.38), producing a somewhat more complicated flow field than is found with a single rotor, and this interacting flow incurs a loss of net rotor system aerodynamic efficiency. Coleman (1993) gives a good summary of coaxial helicopter rotors and a comprehensive list of relevant citations on performance, wake characteristics and methods of analysis.
Following Payne (1959), consider a simple momentum analysis of the hovering coaxial rotor problem. Assume that the rotor planes are sufficiently close together and that each rotor provides an equal fraction of the total system thrust, 2T, where T — W/2. The effective induced velocity of the rotor system will be
Therefore, the induced power is
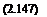 (2 Tf/2
(2 Tf/2
(Pdm = 2 T(Vi)e =
However, if we treat each rotor separately then the induced power for either rotor will be T Vi and for the two separate rotors
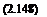 2 T3/2 +j2pA
2 T3/2 +j2pA
If the interference-induced power factor /Cint is considered to be the ratio of Eqs. 2.147 and 2.148 then
which is a 41% increase in induced power relative to the power required to operate the two rotors in complete isolation.
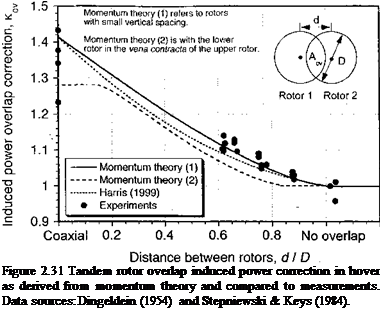
This simple momentum analysis of the problem has been shown to be overly pessimistic when compared with experimental measurements for closely spaced coaxial rotors – see Harrington (1951) and the review by Coleman (1993). The main reason for the overprediction of induced power is related to the actual (finite) spacing between the two rotors. Generally, on coaxial designs the rotors are spaced sufficiently far apart that the lower rotor operates in the vena contracta of the upper rotor. This is justified from the flow visualization results of Taylor (1950), for example. Based on ideal flow considerations, this
|
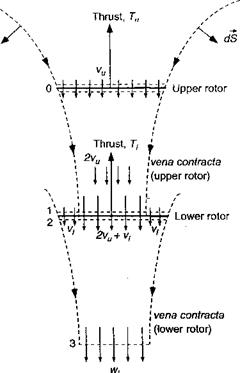
Figure 2.27 Flow model for a coaxial rotor analysis, where the lower rotor is considered to operate in the fully developed slipstream of the upper rotor.
|
means that only half of the area of the lower rotor operates in an effective climb velocity induced by the upper rotor.
This problem can be tackled by means of the simple momentum theory and the application of the mass, momentum, and energy conservation equations in integral form. We will assume that the performance of the upper rotor is not influenced by the lower rotor. The induced velocity at the upper rotor is
= ^ = (2.150)
where A is the disk area and T is the thrust on the upper rotor. The vena contracta of the upper rotor is an area of A/2 with velocity 2vu. Therefore, at the plane of the lower rotor there is a velocity of 2vu + Vi over the inner one-half of the disk area – see Fig. 2.27.
Over the outer one-half of the disk area, the induced velocity is V[. Assume that the velocity in the fully developed slipstream of the lower rotor (plane 3) is uniform with velocity wi. The mass flow rate through the upper rotor is pAvu, so that the momentum exiting in the slipstream of the upper rotor is (pAvu)2vu =2pAv%. This is the momentum of the fluid into the lower rotor. The mass flow rates over the inner and outer parts of the lower rotor are p(A/2)(2vu + V[) and p{A/2)vi, respectively. Therefore,
The momentum flow out of plane 3 is mw/, so the thrust on the lower rotor is Ti = pA(vu + Vi) wi – 2pAv2u.
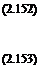
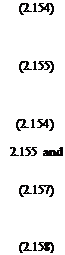 The work done by the lower rotor is
The work done by the lower rotor is
Pi = Tiivu + vt),
and this is equal to the gain in kinetic energy of the slipstream. Therefore,
1 , 1 fA
Ti(vu – f-vt) = – pA(vu + vi) wi ~ 2Pl) (2v“K2l)u
= ^pA(vu + vi)wf – 2pAv3u.
Assuming Ti — Tu = T, then T = 2pAv^, then from Eq. 2.152 we get
Tt = T = ]^pA(vu + vi)wi, and from Eq. 2.154 we get
T(2vu + vi) = ~pA(vu + vi)wf.
Using Eqs. 2.155 and 2.156 gives wt = 2vu + t’/ and substituting this into Eq. remembering that T = 2pAv^ gives
4pAv = pA (vu + vi) W[ = pA (vu 4- vt) (2vu + vt).
Rearranging as a quadratic in terms of vi and solving gives
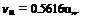 -3 + VI7′
-3 + VI7′
vi =
The power for the upper rotor is Pu = Tvu = Tvh and for the lower rotor Pi = T{vu + v{) = 1.5616Tvh. Therefore, for both rotors the total power is 2.5616ГVh – This is compared to 2T Vh when the rotors are operating in isolation. This means that the induced power factor from interference, /c;nt, is given by
which is a 28% increase compared to a 41% increase when the two rotors have no vertical separation (see Questions 2.19 and 2.20). This is closer to the values deduced from experiments for which Kmt ^ 1.16 [see, for example, Dingeldein (1954)] but the theory still overpredicts the interference value. When the coaxial is operated at equal rotor torque (see Question 2.20), it can be shown that the induced power factor is given by
which is the same result as for the thrust balanced case when compared to two isolated rotors operated at the same thrust. When compared to two isolated rotors at the thrusts needed for a torque balance, then /c;nt = 1.266.
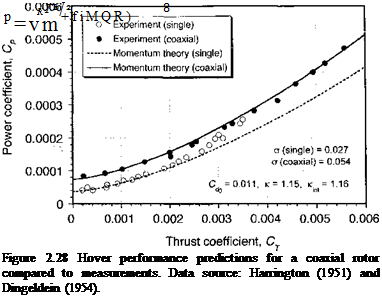
Figure 2.28 shows the power versus thrust relationship of single and coaxial rotors operating in hover; the measurements are taken from Harrington (1951) and Dingeldein
(1954). The corresponding plot of figure of merit versus Ct/o is shown in Fig. 2.29. The power for the single two-bladed rotor was calculated from momentum theory using
and for the coaxial using
with к = 1.15 and к-ш = 1.16. The agreement between momentum theory and the measurements is good and confirms that the coaxial rotor operates as two isolated rotors but with an interference effect accounted for by /qnt. In this case the performance of both the single and coaxial rotors is stall-limited because of their relatively low solidity and also the lower blade chord Reynolds numbers at this reduced tip speed test (see Chapter 7), but the momentum theory shows what would be possible if stall was not present. Clearly the coaxial achieves a somewhat lower maximum figure of merit compared to a single rotor, all other factors being equal (i. e., when compared at the same disk loading, solidity and tip speed).
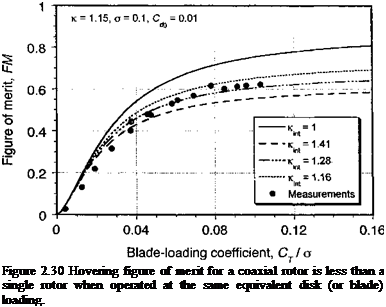
To properly compare the relative efficiency of a single and coaxial rotor system they must be compared at the same equivalent disk loading, that is, each rotor operates at the same approximate value of Т/ A (or Ст/сг for a given radius and tip speed). Under these conditions the figure of merit of the coaxial can be written as
where Kmt = 1 f°r an isolated single rotor. Because the lower rotor of a coaxial operates in the slipstream of the upper rotor its net induced velocity is always higher for a given value
0.
8 –
of thrust and /Cjnt > 1 (where the values of icmt depend on the assumptions made) and so the net system efficiency is lower. Representative results are shown in Fig. 2.30 where it is clear that at a typical operating state the FM for a coaxial when operated at the same blade loading coefficient is related approximately to the corresponding FM of a single by a factor Kint. Other physical factors that seem to affect coaxial rotor performance include a thrust recovery effect through the removal of swirl losses in the downstream wake, although this effect seems only important at very high values of disk loading such as used on propellers. See also Andrew (1981), Saito & Azuma (1981), and Zimmer (1985) for more details on coaxial rotor performance.
![]()
![]() dm = pdA(Vc + Vi) = 2np(Vc + Vi)y dy, so that the incremental thrust on the annulus is
dm = pdA(Vc + Vi) = 2np(Vc + Vi)y dy, so that the incremental thrust on the annulus is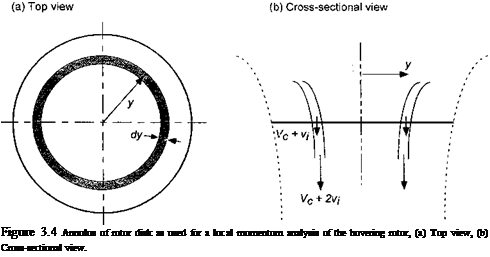
![]()













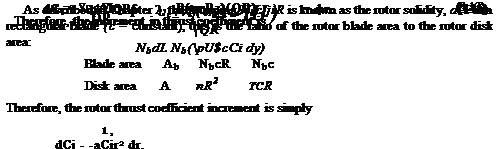
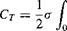 (3.17)
(3.17)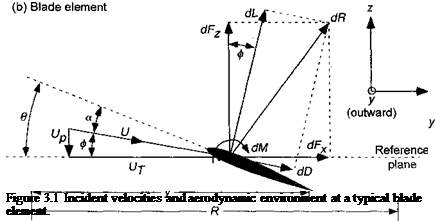
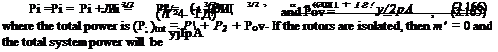

 Tu = (p Avu)(2vu)
Tu = (p Avu)(2vu)
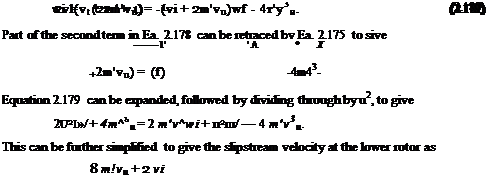

 The work done by the lower rotor is
The work done by the lower rotor is