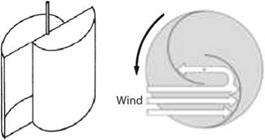
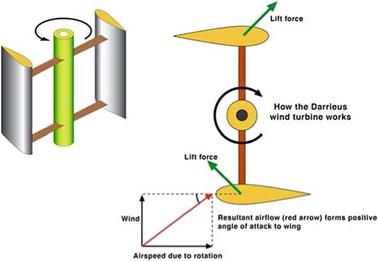
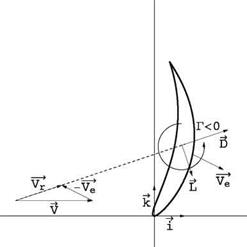
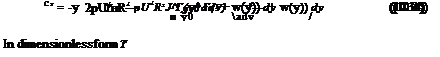Consider a rotor rotating at speed Q, placed in an incoming uniform flow with velocity V = (U, 0, 0) aligned with the turbine axis. We neglect the tower interference on the rotor flow. In a frame of reference attached to the rotor, the flow is steady. The tip speed ratio is defined as TSR = QR/U = 1/adv, which is also the inverse of the advance ratio, adv used as main parameter for propellers. Other dimensionless quantities are defined and used below:
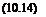
x = Rx, y = Ry, z = Rz
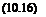
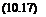 u = Uu, v = Uv, w = Uw
u = Uu, v = Uv, w = Uw
Г = URr
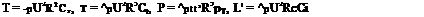 ,3 5,
,3 5,
(10.18)
The bar “-” values correspond to dimensional variables, when the same letter is used. T is the thrust on the tower (N), Ct the thrust coefficient, t is the torque (N. m), Ct the torque coefficient, P the power (W), pT a dimensionless power coefficient, L’ is the local lift force per unit span, and Cl is the local lift coefficient.
Each vortex sheet such as that in Fig. 10.8 is discretized as a lattice, shown unrolled in Fig. 10.9, to better explain the numerical scheme.
The circulation Д j is located at the grid points of the lattice (indicated by the circles). The blade is represented by a lifting line along the y-axis for blade 1 (thick solid line) and Д j represents the circulation inside the blade. The small elements of vorticity dl are located between the grid points and correspond either to trailed vorticity (in the x-direction in the presentation of Fig. 10.10) or shed vorticity (in the y-direction) that is present only when the flow is unsteady. When the flow is steady, as assumed here, the circulation is constant along a vortex filament, i. e. Г, j = Д j, Vi = 2,…, ix. The vorticity is given in terms of the differences in

Fig. 10.10 Blade 1 and two trailing vortices—Schematic of Biot-Savart calculation
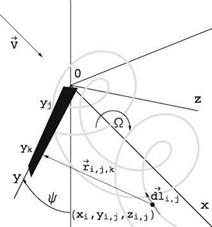
circulation as АД j = Г, j+1_Д j for the trailed vorticity and АГі, j = Г, j_Гі-1, j (=0 here) for shed vorticity. The vortex element orientation is indicated by the arrow which represents positive АД j but the vector components account for the rolling of the sheet on a perfect helix. Let xi, y, zi represent the tip vortex of blade 1
The advance ratio is made to vary linearly from adv1 = (V + u)/QR at the rotor plane і = 1 to advix = (V + 2u)/QR after a few turns of the helix, then remains constant thereafter to the Trefftz plane і = ix. The mesh distribution in the x-direction is stretched from an initial value dx1 at the blade, to some location xstr — 1, using a stretching parameter s > 1 as
xt = xt-i + dxi_i, dxi = sdxi-i, і = 2,…,ix (10.20)
Beyond x = xstr the mesh is uniform all the way to the Trefftz plane xix — 20. In the y-direction, the mesh is discretized with a cosine distribution
1 j _ 1
yj = У0 + 2 (1 _ У0) cos в j, Q j = — – n, j = 1,…, jx (10.21)
2 jx 1
The trailed vortices are located between the mesh lines according to
1 2 j _ 1
П j = У0 + 2 (1 _ У0) cos в j, в j = —— —n, j = 1,…, jx _ 1 (10.22)
2 2(jx 1)
Accounting for the rolling of the sheet on a perfect helix, a small element of trailed vorticity has components
~ctl = {dxi, dyi, j, dzi, j}
 1 1 1
1 1 1
-2(xi+1 – xi-1), -2(yi+1 – yi-1)nj, -2(zi+1 – zi-1)nj
whereas, a small element of shed vorticity has components
~dl = {dxi, dyi, j, dzi, j } = |0, 2 (yi-1 + yi )(nj – nj-1), 2(zi-1 + Zi )(nj – nj-1)
(10.24)
Application of the Biot-Savart formula provides the influence coefficients for the small elements, which are accumulated and stored in multidimensional arrays.
A particular treatment is made for the trailed elements closest to the lifting line and at the Trefftz plane. The former extend only half a cell with origin at 2 (x1 + x2) (see Fig. 10.9), and the latter extend from to to 2(xix-1 + xix), where a remainder accounts for the contribution downstream of the Trefftz plane. Note that in the case of the three-bladed rotor, the lifting lines themselves induce velocities on the other two (but not on themselves as straight blades). The same discretization applies for the calculation of the lifting line contributions for a three-bladed rotor, but now the small vortex element is located along the lifting line, having components
tl = {0, nj – n j-1, 0} , j = 2,…, jx – 1 (10.25)
in the case of blade 1, and АГ, j = A, j represents the circulation inside the blade.
![]()
![]()
![]() (10.29)
(10.29)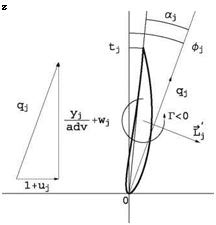 flow configuration
flow configuration