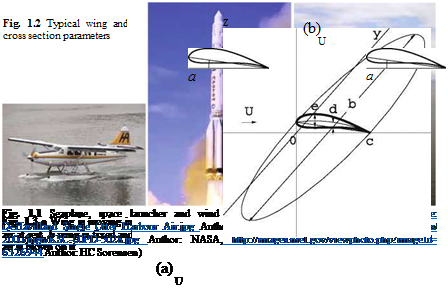
Aerodynamics is the study of the forces on a body in a relative motion with air. Aerodynamics is a subset of fluid mechanics. Other related subjects are hydrodynamics and gas dynamics where the medium is water or gas (at high temperature). In this book we are mainly interested in the aerodynamics of airplanes, also rockets, propellers and wind mills, Fig. 1.1.
Other applications include aerodynamics of cars, trains, ships, sails, buildings and bridges. Aerodynamics applications in technology are of course in turbomachinery (compressors and turbines) and in heating, drying and mixing processes (for example aerodynamics of combustion).
Aerodynamics in nature is manifested in flying birds, also in atmospheric boundary layers, storms, tornadoes and hurricanes and their effects on objects like trees as well as surface erosion and land desertification.
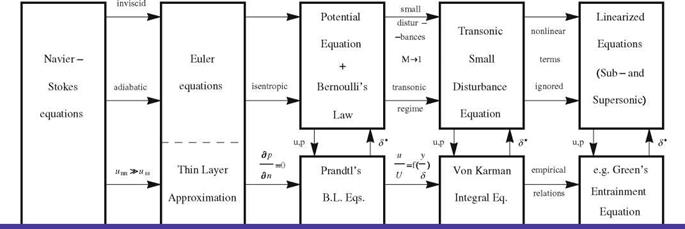
There are three ingredients in any aerodynamic analysis: the geometry of the configuration or the model, the medium or the fluid, and the relative motion or the flow.
Consider an airplane flying in the air and in particular the wing. The geometry of a typical wing can be characterized by the maximum camber d and maximum thickness e of a cross section (airfoil) with maximum chord c and span b, see Fig. 1.2.
The medium (air) can be characterized by certain properties: viscosity coefficient (p), coefficient of heat conductivity (k) and the specific heats cp and cv under constant pressure and constant volume respectively.
For steady flight, as in cruising speed conditions, the flow features including the forces on the body are the same as those obtained if the wing is fixed and air is blown on it. What counts is the relative motion between the body and the particles of the air. Figure1.3 demonstrates the two cases. This observation is the basis of wind tunnel testing. It is easier for analytical and numerical analysis to fix the body and solve the steady state equations in this frame where the variables do not change with time!
The flow can be described in terms of the local velocity vector (V) and the thermodynamic variables: pressure (p), friction (t), density (p) temperature (T)
© Springer Science+Business Media Dordrecht 2015 3
J. J. Chattot and M. M. Hafez, Theoretical and Applied Aerodynamics,
DOI 10.1007/978-94-017-9825-9_1
and pulsation (w) when oscillations are present. The velocity has magnitude and direction. Again what counts is the relative angle between the body axis and the wind (i. e. the same results are obtained if the wind is in the horizontal direction and the wing at angle of attack or the wing is horizontal and the wind inclined with the same angle as shown in Fig. 1.4). In the case of a cambered airfoil, the angle of attack and the camber ratio are the parameters indicative of the flow asymmetry.
Fig. 1.4 Wing at angle of attack
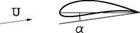 In Tablel.1, the above 13 (or 14) dimensional quantities are summarized together with the corresponding nondimensional parameters. The nondimensional parameters are identified once reference quantities are chosen. For example, the relative camber d, the thickness ratio e and the aspect ratio AR = S a b where S a bc is the area of the wing. The incoming flow velocity U is chosen as reference velocity. The ratio of the specific heats y = cp and the angle of attack a are obviously nondimensional. On the other hand the viscosity and heat conductivity coefficients have different units. A nondimensional parameter of the ratio of viscosity to heat conductivity is introduced as Pr = pr and is called the Prandtl number.
In Tablel.1, the above 13 (or 14) dimensional quantities are summarized together with the corresponding nondimensional parameters. The nondimensional parameters are identified once reference quantities are chosen. For example, the relative camber d, the thickness ratio e and the aspect ratio AR = S a b where S a bc is the area of the wing. The incoming flow velocity U is chosen as reference velocity. The ratio of the specific heats y = cp and the angle of attack a are obviously nondimensional. On the other hand the viscosity and heat conductivity coefficients have different units. A nondimensional parameter of the ratio of viscosity to heat conductivity is introduced as Pr = pr and is called the Prandtl number.
The ratio of the speed of the body (or the wind) U to the speed of sound a is called the Mach number, M = U (where a = VyRT = for a perfect gas). The Mach number represents the compressibility effects.
The ratio of the normal stress (pressure p) to the tangential stress (friction т) is related to the Reynolds number Re a —. The conventional definition is Re = PU. The Reynolds number represents the ratio of inertia to viscous stress as well. The flow oscillations are characterized by the Strouhal number St = Ц-. The result for pressure or shear stress depends on the parameters via a dimensional relationship of the form
p (or т) = f (b, c, d, e, cp, cv, k, p, T, U, p, w, a)
The study of aerodynamics is mainly to find the nondimensional stresses:
• the pressure coefficient Cp = prpr^f
• the skin friction coefficient Cf = – rL
2 pU
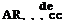
as functions of the nondimensional parameters of flight representing the geometry, the medium and the motion, i. e.
|
Table 1.1 Dimensional quantities and nondimensional parameters
|
Dimensional quantities
|
Nondimensional parameters
|
|
Model
|
b, c, d, e
|
AR, d, c
|
|
Medium
|
cp, Cv, k, p
|
Y, Pr
|
|
Motion
|
T, V, p, w, p, (or т)
|
M, Re, St, a, Cp, (or Cf)
|
|
Notice in the definition of Cp, indicates the atmospheric pressure and 1 pU2 is called the dynamic pressure. (Cp should not be confused with cp, the latter being the specific heat under constant pressure.)
The relation given above is consistent with the Buckingham PI theorem. Since we have four basic units (length, time, mass and temperature) and 13 (or 14) dimensional quantities, hence there are at least 9 (or 10) nondimensional parameters, in fact 10 (or 11) since a is already a dimensionless parameter.
Integration of surface stresses provides the moment about a point (or an axis) and the forces, the lift, and the drag (the force normal and in the flow direction respectively).
Our study is limited to small angles of attack, relative cambers and thickness ratios, i. e. |a| ^ 1, |d | ^ 1 and | ^ 1. Moreover, 7 and Pr are constants. For air, under normal conditions, 7 = 1.4 and Pr = 0.72.
Three types of wings are of interest: high and low aspect ratio wings and their limits, two dimensional and axisymmetric bodies, as well as wings of aspect ratio of order one.
The Mach number range includes constant density, incompressible flow (M = 0 not because V is zero, but because a is large) and compressible subsonic M < 1, transonic M ~ 1 and supersonic flows M > 1. A short introduction of hypersonic flows, M > 1 is presented but rarefied gas dynamics is not included in this book.
Only high Reynolds number flows are of interest in conventional aerodynamics including laminar, transitional and turbulent flows, depending on critical values of Reynolds number.
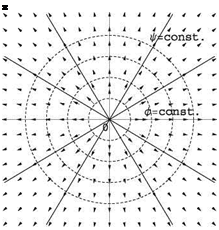
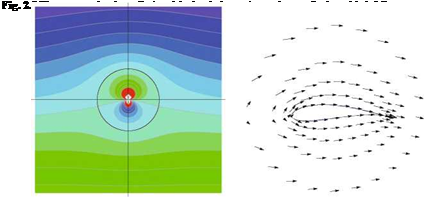
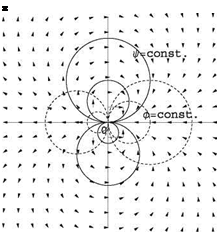 Fig. 2.6 Doublet: equipotential lines and streamlines
Fig. 2.6 Doublet: equipotential lines and streamlines![]() – D cos в – D sin в
– D cos в – D sin в![]() r
r











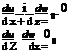 (2.1)
(2.1)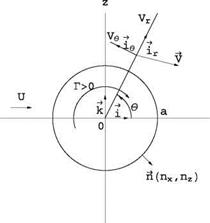 Fig. 2.2 Coordinate system and notation
Fig. 2.2 Coordinate system and notation