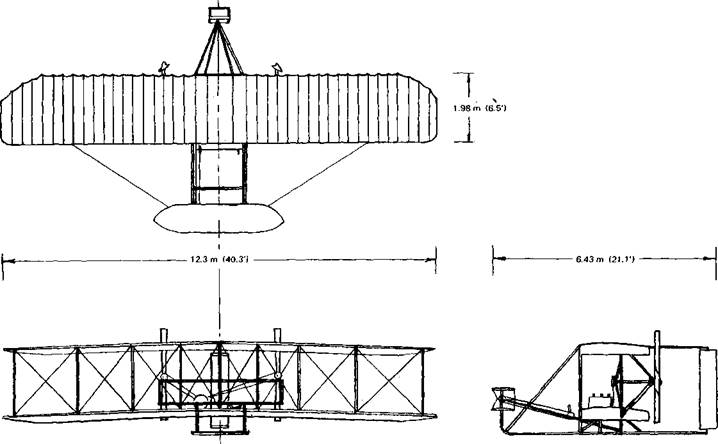
Consider the airplane in steady, climbing flight shown in Figure 1.3. The term steady means that the airplane is not accelerating; hence, all forces and moments on the aircraft must be in balance. To be more precise, one states that the vector sum of all forces and moments on the airplane must be zero. To depict the angles more clearly, all forces are shown acting through the center of gravity (eg). Although the resultant of all the forces must pass
|
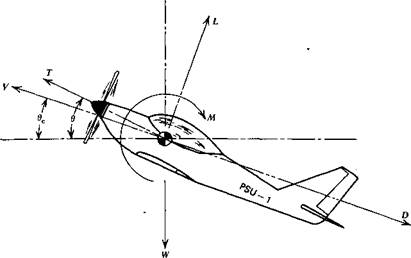
Figure 1.3 Forces and moments on an airplane in a steady climb.
|
through the center of gravity, it is not generally true that any one of the forces, with the exception of W, must satisfy this condition.
In this figure V represents the velocity vector of the airplane’s center of gravity. This vector is shown inclined upward from the horizontal through the angle of climb, 0C. The angle between the horizontal and the thrust line is denoted as 0. If this line is taken to be the reference line of the airplane, then one states that the airplane is pitched up through this angle. The angle between the reference line and the velocity vector, в – вс, is referred to as the angle of attack of the airplane. Later we will use other angles of attack referenced to the wing geometry; thus, one must be careful in interpreting lift and drag data presented as a function of the angle of attack.
The thrust, T, is the propelling force that balances mainly the aerodynamic drag on the airplane. T can be produced by a propeller, a turbojet, or a rocket engine.
The lift, L, is defined as the component of all aerodynamic forces generated by the aircraft in the direction normal to the velocity vector, V. In level flight this means principally the upward vertical force produced by the wing. Generally, however, it includes the tail and fuselage forces. For example, in landing many aircraft require a downward force on the horizontal tail in order to trim out the nose-down pitching moment produced by the wing flaps. This trimming force can be significant, requiring a wing lift noticeably in excess of the airplane’s weight.
Similar to the lift, the drag, D, is defined as the component of all aerodynamic forces generated by the airplane in the direction opposite to the
velocity vector, V. This force is composed of two principal parts, the parasite drag and the induced drag. The induced drag is generated as a result of producing lift; the parasite drag is the drag of the fuselage, landing gear, struts, and other surfaces exposed to the air. There is a fine point concerning the drag of the wing to be mentioned here that will be elaborated on later. Part of the wing drag contributes to the parasite drag and is sometimes referred to as profile drag. The profile drag is closely equal to the drag of the wing at zero lift; however, it does increase with increasing lift. This increase is therefore usually included as part of the induced drag. In a strict sense this is incorrect, as will become clearer later on.
W is the gross weight of the airplane and, by definition, acts at the center of gravity of the airplane and is directed vertically downward. It is composed of the empty weight of the airplane and its useful load. This latter weight includes the payload (passengers and cargo) and the fuel weight.
The pitching moment, M, is defined as positive in the nose-up direction (clockwise in Figure 1.3) and results from the distribution of aerodynamic forces on the wing, tail, fuselage, engine nacelles, and other surfaces exposed to the flow. Obviously, if the airplane is in trim, the sum of these moments about the center of gravity must be zero.
We know today that the aerodynamic forces on an airplane are the same whether we move the airplane through still air or fix the airplane and move the air past it. In other words, it is the relative motion between the air and airplane and not the absolute motion of either that determines the aerodynamic forces. This statement was not always so obvious. When he learned of the Wright Brothers’ wind tunnel tests, Octave Chanute wrote to them on October 12, 1901 (Ref. 1.1) and referred to “natural wind.” Chanute conjectured in his letter:
“It seems to me that there may be a difference in the result whether the air is impinged upon by a moving body or whether the wind impinges upon the same body at rest. In the latter case each molecule, being driven from behind, tends to transfer more of its energy to the body than in the former case when the body meets each molecule successively before it has time to react on its neighbors. ”
Fortunately, Wilbur and Orville Wright chose to believe their own wind tunnel results.
Returning to Figure 1.3, we may equate the vector sum of all forces to zero, since the airplane is in equilibrium. Hence, in the direction of flight,
T cos (0 — 0C) — D — W sin 0C = 0 (1.1)
Normal to this direction,
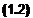 I W cos 6C – L-T sin (0 – вс) = 0
I W cos 6C – L-T sin (0 – вс) = 0
These equations can be solved for the angle of climb to give
In this form, ec appears on both sides of the equation. However, let us assume a priori that вс and (в – вс) are small angles. Also, except for very high performance and V/STOL (vertical or short takeoff and landing) airplanes, the thrust for most airplanes is only a fraction of the weight. Thus, Equation 1.3 becomes
For airplanes propelled by turbojets or rockets, Equation 1.4 is in the form that one would normally use for calculating the angle of climb. However, in the case of airplanes with shaft engines, this equation is modified so that we can deal with power instead of thrust.
First, consider a thrusting propeller that moves a distance S in time t at a constant velocity, V. The work that the propeller performs during this time is, obviously,
work = TS
Power is the rate at which work is performed; hence,
power = T —
But Sit is equal to the velocity of advance of the propeller. Hence the power available from the propeller is given by
P avail = TV (1.5)
Similarly, the power required by a body traveling through the air with a velocity of V and having a drag of D will be
Preqd = DV
Thus, returning to Equation 1.4, by multiplying through by WV, we get
W(Vec) = P a vail — Preq’d (1-6)
The quantity V0C is the vertical rate of climb, Vc. The difference between the power that is required and that available is referred to as the excess power, Pxs – Thus Equation 1.6 shows that the vertical rate of climb can be obtained by equating the excess power to the power required to lift the airplane’s weight at the rate Vc. In operating an airplane this means the following. A pilot is flying at a given speed in steady, level flight with the engine throttle only partially open. If the pilot advances the throttle while maintaining a
constant airspeed, the power from the engine will then be in excess of that required for level flight, and the airplane will climb.
Suppose, instead of keeping it constant, the pilot, while opening the throttle, allows the airspeed to increase in such a manner as to maintain a constant altitude. When a wide open throttle (WOT) condition is reached the maximum power available is equal to the power required. This is the condition for maximum airspeed, “straight and level.”
From this brief introduction into airplane performance, it is obvious that we must be able to estimate the aerodynamic forces on the airplane before we can predict its performance. Also, a knowledge of the characteristics of its power plant-propulsor combination is essential.
In addition to performance, the area of “flying qualities” is very important to the acceptance of an airplane by the customer. Flying qualities refers primarily to stability and control, but it also encompasses airplane response to atmospheric disturbances.
Let us briefly consider the pitching moment M, shown in Figure 1.3. This moment, which must be zero for steady, trimmed flight, results mainly from the lift on the wing and tail. In addition, contributions arise from the fuselage, nacelles, propulsor, and distribution of pressure over the wing. Suppose now that the airplane is trimmed in steady, level flight when it is suddenly disturbed (possibly by a gust or an input from the pilot) such that it pitches up by some amount. Before it can respond, the airplane’s path is still essentially horizontal, so that the angle between the velocity vector and the plane’s axis is momentarily increased. It will be shown later that, at a given airspeed, the moment, M, is dependent on this angle, defined previously as the angle of attack. Since the moment was initially zero before the airplane was disturbed, it follows that, in general, it will have some value other than zero due to the increase in angle of attack. Suppose this increment in M is positive. In this case the tendency would then be for the angle of attack to increase even further. This is an unstable situation where the airplane, when disturbed, tends to move even further from its steady-state condition. Thus, for the airplane to exhibit a more favorable, stable response, we desire that the increment in M caused by an angle of attack change be negative.
This is about as far as we can go without considering in detail the generation of aerodynamic forces and moments on an airplane and its components. The preceding discussion has shown the importance of being able to predict these quantities from both performance and flying qualities viewpoints. The following chapters will present detailed analytical and experimental material sufficient to determine the performance and stability and control characteristics of an airplane.
As you study the material to follow, keep in mind that it took the early aviation pioneers a lifetime to accumulate only a fraction of the knowledge that is yours to gain with a few months of study.
The primary system of units to be used in this text is the SI (Systems Internationale) system. Since this system is just now being adopted in the United States, a comparison to the English system is presented in Appendix A. l. Also, to assure familiarity with both systems, a limited number of exercises are given in the English system. For a more complete explanation of the SI system, see Reference 1.4.
PROBLEMS
1.1 Calculate the rate of climb of an airplane having a thrust-to-weight ratio of 0.25 and a lift-to-drag ratio of 15.0 at a forward velocity of 70m/s (230 fps). Express Vc in meters per second. Current practice is to express rate of climb in feet per minute. What would be your answer in these units?
1.2
Which of the systems (ball and track) pictured below are in equilibrium? Which are stable?
1.3 An aircraft weighs 45,000 N (10,117 lb) and requires 597 kW (800 hp) to fly straight and level at a speed of 80 m/s (179 mph). If the available power is 895 kW (1200 hp), how fast will the airplane climb when the throttle is advanced to the wide open position?
1.4 For an aircraft with a high thrust-to-weight ratio, the angle of climb is not necessarily small. In addition, for certain V/STOL aircraft, the thrust vector can be inclined upward significantly with respect to the direction of flight. If this angle is denoted as 0T, show that
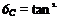 T cos 6t — D L + T sin вт
T cos 6t — D L + T sin вт
1.5 A student pushes against the side of a building with a force of 6N for a period of 4 hr. How much work was done?
1.6 An aircraft has a lift-to-drag ratio of 15. It is at an altitude of 1500 m (4921 ft) when the engine fails. An airport is 16 km (9.94 miles) ahead. Will the pilot be able to reach it?
REFERENCES
1.1 McFarland, Marvin W., editor, The Papers of Wilbur and Orville Wright, Including the Chanute-Wright Letters, McGraw-Hill, New York, 1953.
1.2 Harris, Sherwood, The First to Fly, Aviation’s Pioneer Days, Simon and Schuster, New York, 1970.
1.3 Robertson, James M., Hydrodynamics in Theory and Application, Prentice-Hall, Englewood Cliffs, N. J., 1965.
1.4 Mechtly, E. A., The International System of Units, Physical Constants and Conversion Factors, NASA SP-7012, U. S. Government Printing Office, Washington, D. C., 1969.
1.5 Cleveland, F. A., “Size Effects in Conventional Aircraft Design,” J. of Aircraft, 7(6), November-December 1970 (33rd Wright Brothers Lecture).
TWO
![]() _V_ { [[/(VcaQ/S + l^-‘^-ni1’2 Vca, Г L [f(VCil)+l](1’-Wl’-l JJ
_V_ { [[/(VcaQ/S + l^-‘^-ni1’2 Vca, Г L [f(VCil)+l](1’-Wl’-l JJ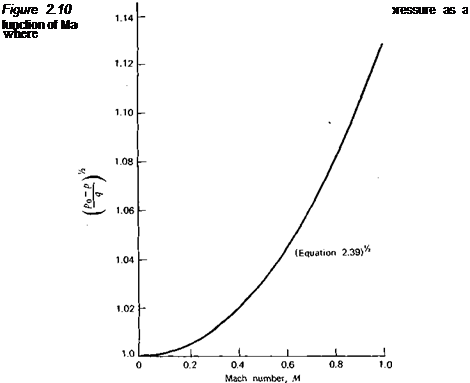
![]() p(Po-p)T/2
p(Po-p)T/2










 But, from continuity, or
But, from continuity, or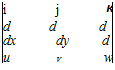 (2-25)
(2-25)
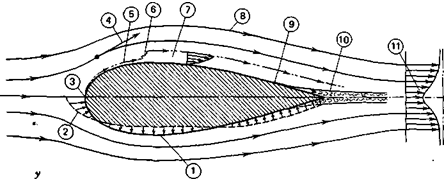
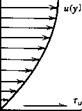 ІШШШІжшшшіш Figure 2.5 Viscous flow adjacent to a surface.
ІШШШІжшшшіш Figure 2.5 Viscous flow adjacent to a surface.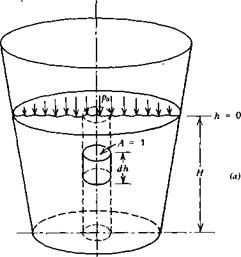


 T cos 6t — D L + T sin вт
T cos 6t — D L + T sin вт