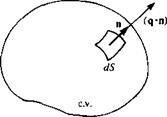
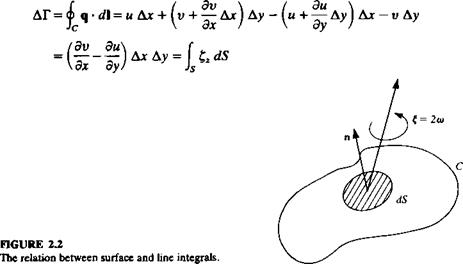
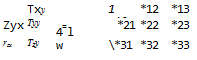Equations (1.15) and (1.19) are the integral forms of the conservation of mass and momentum equations. In many cases, though, the differential representation is more useful. In order to derive the differential form of the conservation of mass equation, both integrals of Eq. (1.15) should be volume integrals. This can be accomplished by the use of the divergence theorem (see Kellogg,13 p39) which states that for a vector q:
f n*q dS = f V*q dV (1-20)
If q is the flow velocity vector then this equation states that the fluid flux through the boundary of the control surface (left-hand side) is equal to the rate of expansion of the fluid (right-hand side) inside the control volume. In Eq. (1.20), V is the gradient operator, and, in cartesian coordinates, is
_ . 3 . 3 3
V = ‘ —+ j —+ k — Эх dy dz
і
where e; is the unit vector (i, j, k, for j = 1, 2, 3). Thus the indicial form of the divergence theorem becomes
An application of Eq. (1.20) to the surface integral term in Eq. (1.15) transforms it to a volume integral:
This allows the two terms to be combined as one volume integral: where the time derivative is taken inside the integral since the control volume is stationary. Because the equation must hold for an arbitrary control volume anywhere in the fluid, then the integrand is also equal to zero. Thus, the following differential form of the conservation of mass or the continuity equation is obtained:
 — + V • pq = 0 3t
— + V • pq = 0 3t

|
and in cartesian coordinates:
Эр Эр Эр Эр /Эи dv ЗиЛ
~si + “3/+V^+Wl~z*,’J/ + Ty+^)~0 By using the material derivative
|
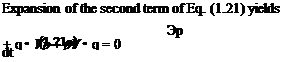 |
|
|
|
D д „ Э Э Э Э 7Г s – r + q • V = — + и — + v — + tv — Dt dt dt dx dy dz
|
|
|
|
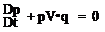 |
|
|

The material derivative D/Dt represents the rate of change following a fluid particle. For example, the acceleration of a fluid particle is given by
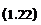 Dq dq
Dq dq
a = -3 = -3 + q • Vq Dt dt 4 4
An incompressible fluid is a fluid whose elements cannot experience volume change. Since by definition the mass of a fluid element is constant, the fluid elements of an incompressible fluid must have constant density. (A homogeneous incompressible fluid is therefore a constant-density fluid.) The continuity equation (Eq. (1.21)) for an incompressible fluid reduces to
Note that the incompressible continuity equation does not have time derivatives (but time dependency can be introduced via time-dependent boundary conditions).
To obtain the differential form of the momentum equation, the divergence theorem, Eq. (1.20a), is applied to the surface integral terms of Eq.
(1.19) :
|
f РЯіІЧ • n) dS = І V • pqtq dV
■*C. S. Jc. v.
[ HjTij ds=[ dV
■’c. s. Л v. dX-j
|
Substituting these results into Eq. (1.19) yields
Since this integral holds for an arbitrary control volume, the integrand must be zero and therefore
jt(pqi) + V’pqiq = pfi+^ 0 = 1,2,3) (1.25)
Expanding the left-hand side of Eq. (1.25) first, and then using the continuity equation, will reduce the left-hand side to
Jf (Mi) + V * (РЧіЧ) = <?«[^ + V • pqj + p|+ q • Vq,] = p^
(Note that the fluid acceleration is
which according to Newton’s second law when multiplied by the mass per volume must be equal to E fi )
So, after substituting this form of the acceleration term into Eq. (1.25), the differential form of the momentum equation becomes pa, = E Ft or:
P^ = p/; + |f 0 = 1.2,3) (1.26)
and in cartesian coordinates:
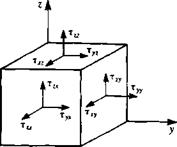
 (Эи Эм,3м, Эи v дтхх дтху дтх2
(Эи Эм,3м, Эи v дтхх дтху дтх2
РI + и Т + v + w Т – = 2. F* = Pf* + Т~ + а +
V dt Эх ду dzl Эх ду Эг
(dv dv dv dv v-, г – .. дтху дХуу Зт
Р Ьг + и — + v — + ^ — = 2,Fy = Pfy+-^- + ~т – + -^г£
H5t Эх Эу dzJ ^ у у Эх ду Эг
(dw 3w dw ЗиЛ v дтХ2 дГу2 дтгг
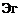 Ча+“* + "* + "й)-2р-‘*- + -аГ+*-+
Ча+“* + "* + "й)-2р-‘*- + -аГ+*-+
For a Newtonian fluid the stress components т, у are given by Eq. (1.10), and by substituting them into Eqs. (1.26a-c), the Navier-Stokes equations are obtained:
(/ = 1, 2, 3)
and in cartesian coordinates:
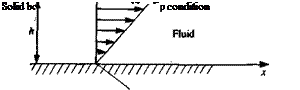
FIGURE 1.9
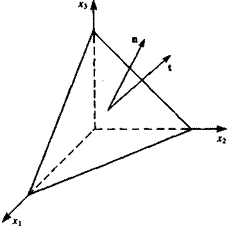
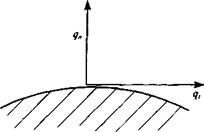 Direction of tangential and normal velocity components near a solid boundary.
Direction of tangential and normal velocity components near a solid boundary.
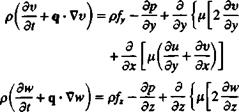
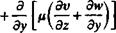 dy> (1.27b)
dy> (1.27b)
(1.27c)
Typical boundary conditions for this problem require that on stationary solid boundaries (Fig. 1.9) both the normal and tangential velocity components will reduce to zero:
q„-0 (on solid surface) (1.28a)
q, = 0 (on solid surface) (1.28b)
The number of exact solutions to the Navier-Stokes equations is small because of the nonlinearity of the differential equations. However, in many situations some terms can be neglected so that simpler equations can be obtained. For example, by assuming constant viscosity coefficient p, Eq. (1.27) becomes
p(^ + 4 • Vq) = pf – Vp + juV2q +1 V(V • q) (1.29)
Furthermore, by assuming an incompressible fluid (for which the continuity equation (Eq. (1.23)) is V • q = 0), Eq. (1.27) reduces to
p(|j + q-Vq) = pf~Vp+ pV2q (1-30)
For an inviscid compressible fluid:
^ + q • Vq = f — — (1.31)
at p
This equation is called the Euler equation.

|
FIGURE 1.10
Cylindrical coordinate system.
|
|
|
In situations when the problem has cylindrical or spherical symmetry, the use of appropriate coordinates can simplify the solution. As an example, the fundamental equations for an incompressible fluid with constant viscosity are presented. The cylindrical coordinate system is described in Fig. 1.10, and for this example the г, в coordinates are in a plane normal to the x coordinate. The operators V, V2 and D/Dt in the г, в, x systems are (see Pai,14 p. 38 or Yuan,12 p. 132)
|
|
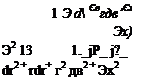 |
|
|
|
|
|
|
|
The continuity equation in cylindrical coordinates for an incompressible fluid then becomes
|
|
|
dqr ldqe, dqx | qr_Q dr г дв Эх г
The momentum equation for an incompressible fluid is r direction:
|
|
|
|
|
(Dqr q\_. dP. Jrfl„ 2 3?e
PVN~Т) = + (L36)
|
|
|
|
|
|
|
p£3±=pf il+p
У Dt И Эх И 4
|
|
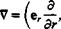
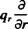

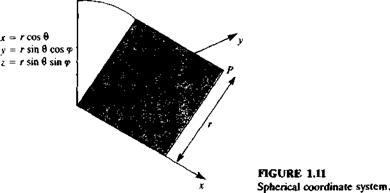
A spherical coordinate system with the coordinates г, d, <p is described in Fig. 1.11. The operators V, V2 and D/Dt in the г, d, <p system are (Karamcheti,15 chapter 2, or Yuan,12 p. 132)
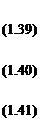 „ / э ід і э
„ / э ід і э
^ a >®e aa ’ ®,p a a )
dr r da r sin в dtp!
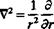 (2d 1 d ( . d 1 Э2
(2d 1 d ( . d 1 Э2
V dr) + r2 sin в dd ,n dd) + r2 sin2 в dip2
R = l + a 3 Яв 3 3
Dt dt "r dr r dd r sin d d<p
The continuity equation in spherical coordinates for an incompressible fluid becomes (Pai,14 p. 40)
1 d(r2qr) 1 d(ge sin d) | 1 Q
r dr sin d dd sin d dqp
The momentum equation for an incompressible fluid is (Pai,14 p. 40): r direction :
Щг q% + q2e. f _$P
dr
. Mr 2 9qe 2qe cot в 2 dqv
+ ———— – —— (1.43)
d direction :
(Ще, ЧгЧв ЧІcot в _ „г 1 дР р(-5Г + ~ 7 )~р1‘~~гэв
( 2 2 dqr qe 2 cos d dqЛ
+ ^ r2 dd r2sin2 0 r2sin20 3<p/
FIGURE 1.12
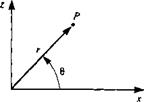 Two-dimensional polar coordinate system.
Two-dimensional polar coordinate system.
(p direction:
Dq<r qvqr qeqv cot fl ^ і Ф
£)/ /• r / ^v r sin 0 dtp
(V2 Чя> . 2 дЯг. 2 cos e dqe
‘4v^ r2 sin2 O r2 sin 0 3® r2 sin2 в dw ) (145)
When a two-dimensional flow field is treated in this text, it will be described in either a cartesian coordinate system with coordinates x and z or in a corresponding polar coordinate system with coordinates r and в (see Fig. 1.12). In this polar coordinate system, the continuity equation for an incompressible fluid is obtained from Eq. (1.35) by eliminating dqx/dx and the r – and 0-momentum equations for an incompressible fluid are identical to Eqs.
(1.36) and (1.37), respectively.
![]()
![]() (2.14)
(2.14)











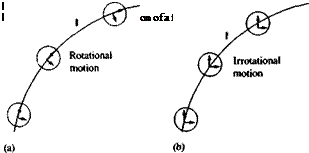
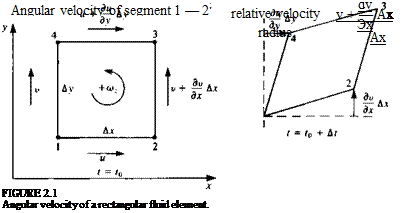
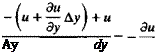
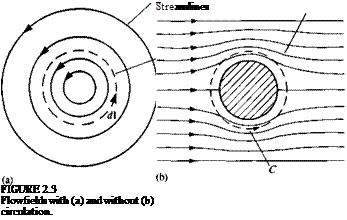
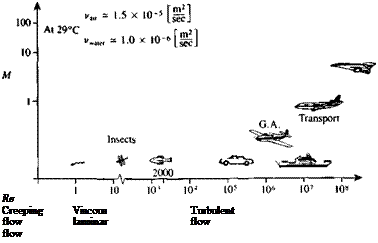
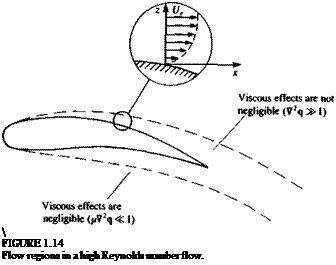
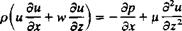 (1.64)
(1.64)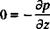 (1.65)
(1.65)
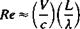
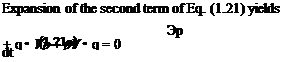
 (Эи Эм,3м, Эи v дтхх дтху дтх2
(Эи Эм,3м, Эи v дтхх дтху дтх2 Direction of tangential and normal velocity components near a solid boundary.
Direction of tangential and normal velocity components near a solid boundary.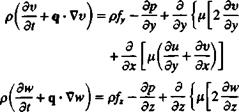
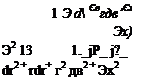



 Two-dimensional polar coordinate system.
Two-dimensional polar coordinate system.