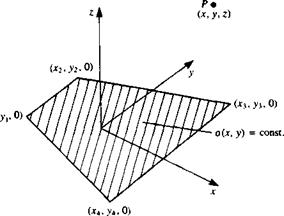
Constant-Strength Vortex Line Segment
Early numerical solutions for lifting flows were based on vortex distribution solutions of the lifting surface equations (Section 4.5). The three-dimensional solution of such a problem is possible by using constant-strength vortex line segments, which can be used to model the wing or the wake. The velocity induced by such a vortex segment of circulation Г was developed in Sections 2.11-2.12 and Eq. (2.68b) states
If the vortex segment points from point 1 to point 2, as shown in Fig. 10.23,
 FIGURE 10.19
FIGURE 10.19
Comparison between the velocity induced by a rectangular source element and an equivalent point source along a horizontal survey line (median).
FIGURE 10.20
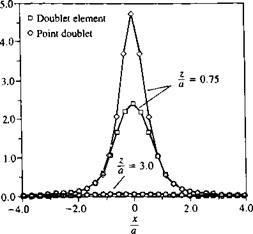
 Comparison between the velocity induced by a rectangular doublet element and an equivalent point doublet along a horizontal survey line (median).
Comparison between the velocity induced by a rectangular doublet element and an equivalent point doublet along a horizontal survey line (median).
then the velocity at an arbitrary point P can be obtained by Eq. (2.72):
![]() „ – Г Г1 X r2 (t! Г2
„ – Г Г1 X r2 (t! Г2
1,2 4я|гіХг2|2Го rj r2)
For a numerical computation in a cartesian system where the (jc, y, z) values of the points 1,2, and P are given, the velocity can be calculated by the following steps:
1. Calculate X r2:
(Гі X r2), = (yp – y,)(zp – z2) – (zp – z,)(yp – y2)
(г, X r2)y = -(Xp – X)(zp – z2) – (zp – z,)(xp – x2)
(ri x r2), = (xp – х^ІУр – y2) – (yp – Уі)(хр – x2)
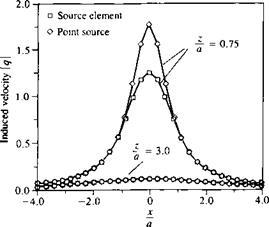 FIGURE 10.21
FIGURE 10.21
Comparison between the velocity induced by a rectangular source element and an equivalent point source along a horizontal survey line (diagonal).
FIGURE 10.22
![]()
 Comparison between the velocity induced by a rectangular doublet element and an equivalent point doublet along a horizontal survey line (diagonal).
Comparison between the velocity induced by a rectangular doublet element and an equivalent point doublet along a horizontal survey line (diagonal).
Also the absolute value of this vector product is
ki x r2|2 = (rt X r2)2 + (г, X r2)2 + (Гі X r2)2
2. Calculate the distances ru r2:
П = У/(хр – x,)2 + (yp – y,)2 + (z„ – zxf r2 = VC*p – X2)2 + (yp – y2f + (zp – Z2f
3. Check for singular conditions. (Since the vortex solution is singular when the point P lies on the vortex. Then a special treatment is needed in the vicinity of the vortex segment—which for numerical purposes is assumed to have a very small radius e)
IF (ru or r2, or Iг! X r2|2 < e)
where € is the vortex core size (which can be as small as the truncation error)
 |
THEN (M = v = w = 0)
or else u, v, w, can be estimated by assuming solid body rotation or any other (more elaborate) vortex core model (see Section 2.5.1 of Ref. 10.3).
4. Calculate the dot-product:
*b * r, = (X2 – x^iXp – Xi) + (y2 – уЖур – Ух) + (z2 – Z)(zp – Zi)
Го r2 = (x2 – Xi)(xp – x2) + (y2 ~ УїХУр – Уг) + (z2 – z^)(zp – z2)
5. The resulting velocity components are
и = X(rt x r2)x v = K(tt x i2)y w = K( rt x r2)2
where
![]()
For computational purposes these steps can be included in a subroutine (e. g., VORTXL—vortex line) that will calculate the induced velocity (и, v, w) at a point P(x, y, z) as a function of the vortex line strength and its edge coordinates, such that
![]()
As an example for programming this algorithm see subroutine VORTEX (VORTEX = VORTXL) in Program No. 12 in Appendix D.











 Survey lines for the velocity induced by a rectangular, flat element.
Survey lines for the velocity induced by a rectangular, flat element.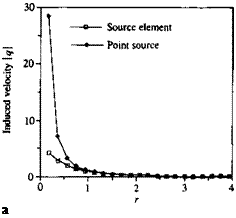 FIGURE 10.17
FIGURE 10.17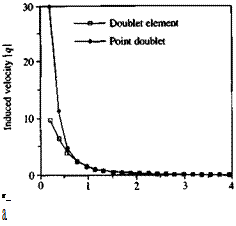 Comparison between the velocity induced by a rectangular doublet element and an equivalent point doublet versus height rja.
Comparison between the velocity induced by a rectangular doublet element and an equivalent point doublet versus height rja.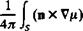 f diX
f diX
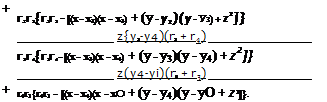

 Ф(х, у, z) = z[(x – x0f + (y – y0f + z2]-3’2
Ф(х, у, z) = z[(x – x0f + (y – y0f + z2]-3’2
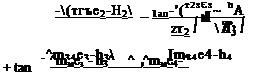
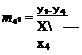

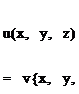 ________ oA(x – x0)________
________ oA(x – x0)________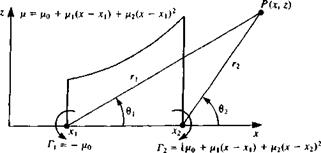

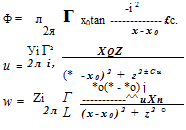 (10.68)
(10.68) Ф=±^(х2-х2)
Ф=±^(х2-х2)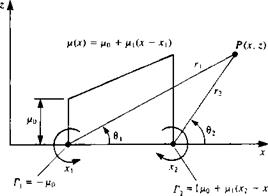 FIGURE 10.12
FIGURE 10.12


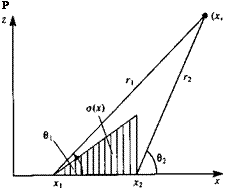 Nomenclature for calculating the influence of linearly varying strength source.
Nomenclature for calculating the influence of linearly varying strength source.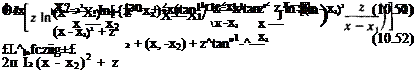
 -£<*М-г¥!-г)
-£<*М-г¥!-г)