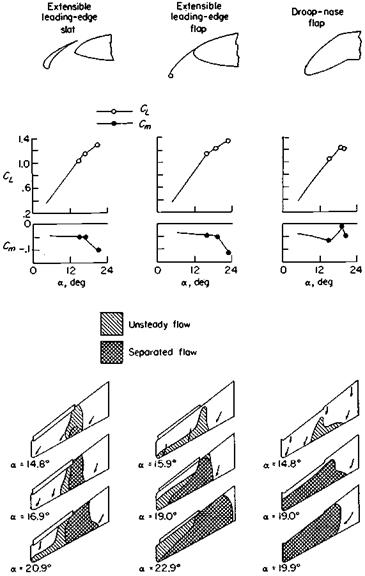
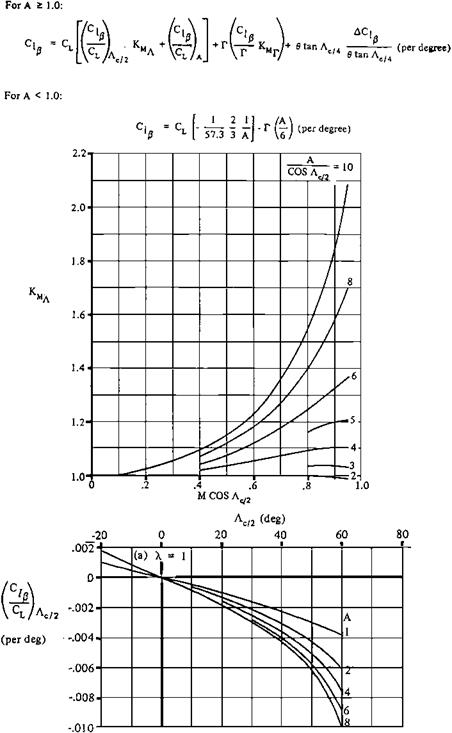
The word “departure” is used for uncontrolled flight following stalls, the first stages of spin entry. Rather violent departures appeared with the advent of swept wings and long, heavily loaded fuselages, the same features that lead to inertial coupling. Pilots reported nose slices, whirling motions, wing rock, and roll reversals and divergences. There was interest almost at once in finding aerodynamic parameters specifically tied to these anomalies.
The initial search led back to stability and control’s early days, a time of high interest in Routh’s criterion and stability boundaries. Lateral stability boundaries are formed from the lateral characteristic equation
X4 + BXi + C Xі + DX + E = 0.
A necessary condition for stability is that the constants B, C, D, and E all be positive in sign. The last two constants, D and E, are associated with real roots, or convergences or divergences, rather than an oscillation.
In the lateral stability boundaries developed by L. W. Bryant in 1932 and by Charles H. Zimmerman in 1937, sign changes in D and E plotted as functions of static lateral and directional stability define the boundaries. Zimmerman specifically associated the constant D with directional divergence.
Two later investigators, Martin T. Moul and John W. Paulson, followed in Bryant’s and Zimmerman’s footsteps, but associated directional divergence with the constant C rather than D. Robert Weissman’s name is also associated with this development (Figure 9.10). Moul and Paulson coined a new term, “dynamic directional stability,” or C„^dyn for an approximation to C. This approximation is
Cnedyn = Cne cos a – (Iz/Ix)Ch sin a.
Together with another factor called “lateral control departure parameter” or LCDP, departures and post-stall gyrations, as well as roll reversals and tendencies to spin, are
|
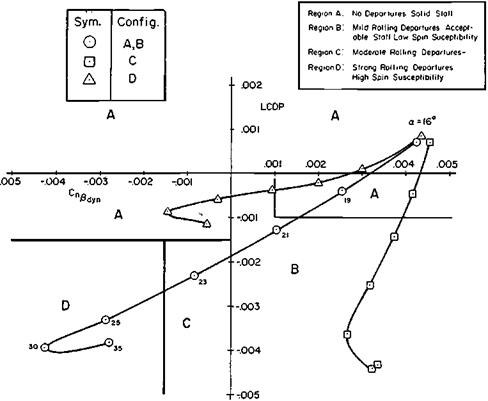
Figure 9.10 The 1972 Weissman spin susceptibility and departure boundaries. The curved lines are parametervalues forthe McDonnell Douglas F-4J and two variants (C and D) with improved departure resistance. (From Mitchell and Johnson, AFWAL-TR-80-3141, 1980)
|
correlated with stability derivatives. LCDP in particular, developed by Pinsker (1967), predicts high angle of attack nose slice departures while the pilot attempts to hold the wings level.
The pioneering work of Moul, Paulson, Pinsker, and Weissman in revisiting the Bryant – Zimmerman concept of stability boundaries for departures and post-stall gyrations was followed by several other noted investigators, who developed additional criteria for departure resistance. Figure 9.11 shows another set of departure and roll-reversal boundaries that are based completely on static aerodynamic derivatives (Bihrle and Barnhart, 1978). The advantage of using static derivatives in setting the boundaries is that they can be applied on the spot during conventional low-speed wind-tunnel tests of a complete model.
The Bihrle boundaries are based on digital simulation of a canned full control deflection maneuver involving an initial steep turn followed by full nose-up pitch control, then full opposite roll control. In papers given in 1978 and 1989, JuriKalviste and Bob Eller proposed coupled static and dynamic stability parameters that are based on separation of the full airplane equations of motion into rotary and translatory sets. These parameters amount to generalizations of the Moul-Paulson C„^dyn and LCDP parameters.
The level of sophistication of this work was raised by use of pilot-in-the-loop considerations, which are treated more fully in Chapter 21, “Flying Qualities Research Moves with the Times.” In the period 1976 to 1980, David G. Mitchell and Donald E. Johnston correlated
|
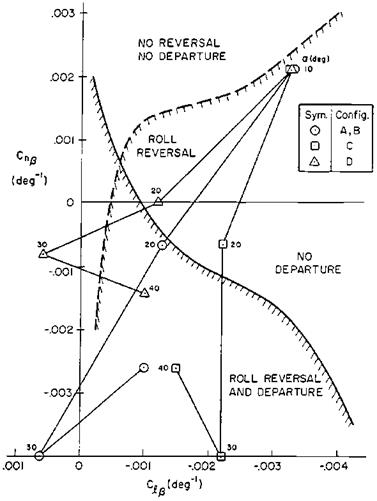
Figure 9.11 The simplified 1978 Bihrie roll reversal and departure boundaries forthe case of adverse yawing moment due to aileron deflection. These simplified boundaries involve static parameters only and can be applied during a routine wind-tunnel test. In configuration A the circles apply to the unmodified McDonnell Douglas F-4J and the other symbols are for F-4J variants. (From Mitchell and Johnston, AFWAL-TR-80-3141, 1980)
|
some departure characteristics with airplane frequency-response parameters involved with pilot loop closures. Negative values of the lateral transfer function numerator term NSa causes roll reversal, for example. Mitchell and Johnston found two additional closed-loop departure parameters for either rudder or aileron maneuvering control that correlate with nose-slice departures.
The vexing question of just how far one can go in using departure criteria based on linearized aerodynamics, or the stability derivatives, is addressed in a paper delivered by Donald Johnston at a1978 AGARD Symposium on Dynamic Stability Parameters. Although the linearized parameters clearly have some predictive value, Johnston concludes:
the more common frequency domain linear analysis techniques applied to symmetric, frozen point airframe models may produce totally erroneous answers if the aircraft exhibits significant coupling due to sideslip. These same analytic techniques provide valid predictions incases where Cm, Cl, Cn are f (а, в) providing the frozen point model represents asymmetric trim conditions and the analytic results are not applied to в excursions through zero.
Calculations on the Vought A-7 airplane provide additional evidence of the importance of sideslip coupling on departures (Johnston and Hogge, 1976). Sideslip angles up to 15 degrees have a moderate stabilizing effect on the Dutch roll and longitudinal short-period modes of motion. However, the spiral and roll modes combine to form a new low-frequency or phugoid-type lateral mode, which is unstable at the higher sideslip angles. A pitch attitude numerator factor, or zero, moves to the right half of the s-plane with sideslip, creating a potential instability with pilot loop closure.
The presence of stability augmentation, such as roll rate feedback to the ailerons, clearly affects departures. Extension of the determinant of the equations of motion to include augmentation feedbacks produces modified departure criteria (Lutze, Durham, and Mason, 1996).
Peter Mangold of Dornier reviewed departure again, to account for the trend toward higher usable angles of attack, where forebody vortices from the nose, strakes, or canards dominate lateral-directional stability. From Mangold’s paper (1991):
For the older aircraft the dynamic [rotary] data were of minor influence and the departure characteristics in Weissman’s correlation were dominated by the static derivatives. High angle of attack characteristics of modern aircraft are more dependent on dynamic derivatives which are heavily influenced by forebody geometry.
Mangold goes on to reaffirm the validity of the Bryant-Zimmerman characteristic equation approach in the modern context and offers four rules to follow to avoid departure, as follows:
1. Avoid autorotation tendency (Clp < 0) and maintain yaw damping (C„r < 0) in order to keep the B coefficient [not Zimmerman’s D or Moul’s C] of the characteristic equation greater than zero.
2. C„edyn must be kept larger than zero, since this parameter determines the C coefficient.
3. Close to maximum lift, where Cir is considerably larger than 1.0, it is essential to maintain C„edyn > 0 with negative Cie and only slightly positive C„e.
4. Nonlinearities and hysteresis effects versus sideslip have to be avoided.
The interesting reason for the fourth rule is the inaccuracy of sideslip sensors at high angles of attack, which makes it difficult to schedule control laws to cope with the problems of nonlinearities and hysteresis.
Recognizing the ingenuity and skill of the developers of departure parameters, it is still possible to question the place of these parameters in modern design practice. Departure parameters such as C„edyn and LCDP may remain of interest in preliminary design. However, in a sense, departure parameter research is working behind the curve of modern computer development. Designers responsible for the stability and control of expensive new airplanes will recognize the essential nonlinearity of the departure and spin problems and plan exhaustive digital simulations to explore the full envelope of flight and loading conditions and control inputs. Automated analysis can stack cases on cases and then winnow out those of no interest by algorithms that scan the results.
There is still the major effort required to build aerodynamic data bases for such enterprises. Furthermore, such efforts would presumably evaluate candidate stability or control augmentation schemes, as well. Augmentation schemes for fly-by-wire systems, such as
used on the Tornado, can produce care-free airplanes that cannot be made to depart under any pilot action. Departure parameters would be of interest after the fact, to help make sense of the results and as a guide to the future.