Departures in Modern Fighters
In spite of the best efforts of designers to apply the departure research lessons of Moul, Paulson, Pinsker, Weissman, and others, fighter airplanes of the F-14, F-15, F-16, and F-18 generation have departure problems. The situation was summarized by the high angle of attack researcher and test pilots, NASA veterans Seth B. Anderson and Einar K. Enevoldson, and the young NASA Langley engineer, Luat T. Nguyen (1983). This is what they reported for specific airplanes:
|
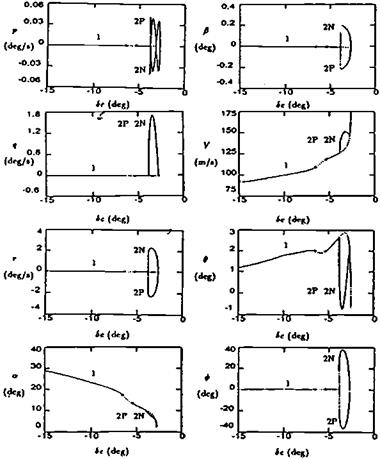
Figure 9.12 System steady states plotted as a function of stabilizer angle for the Grumman F-14A Tomcat. The solid curves, for stabilizer angles more negative (trailing edge up) than —7 degrees, indicate stable trim conditions. Dashed curves for stabilizer angles between —5.4 and —6.7 degrees represent unstable trim points and those between two Hopf bifurcations are represented by the small dots. (From Jahnke and Culick, Jour of Aircraft, 1994) |
Grumman F-14A Mild directional divergence and roll reversal start at an angle of attack of 15 degrees. Divergent wing rock and yaw excursions occur at an angle of attack of 28 degrees in the takeoff and landing configurations. A snap roll series can occur if the airplane is rolled at a high angle of attack. The pilot is located some 22 feet ahead of the airplane’s center of gravity. As a result, if yaw excursions are allowed to build up, cockpit lateral and longitudinal accelerations are high enough to interfere with the pilot’s ability to apply recovery control. A cure for F-14A departures was found by the NASA team, in a switch of roll control at high angles of attack from differential deflection of the horizontal tails to rudder deflection. This feature and foldout canards on the fuselage forebody are used on advanced, digitally controlled F-14As (Chambers, 2000).
General Dynamics F-16A and F-16B Yaw and roll departures are effectively prevented by a system that detects yaw rate above a threshold and automatically appliesspin recovery control: aileronswith and rudder against the yaw. However,
|
Figure 9.13 Transonic yaw departure obtained with a McDonnell Douglas F/A-18A by using prospin controls, or aileron against, and rudder with a turn at a medium angle of attack. (From Anderson, Enevoldson, and Nguyen, AGARD CP-347, 1983) |
an angle of attack limiting system can be defeated in a number of ways, leading to excessive angles of attack.
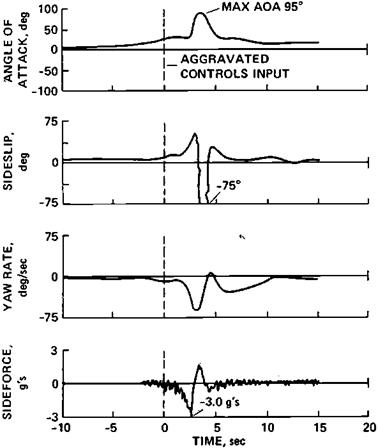
McDonnell Douglas F/A-18A An automatic spin recovery mode, providing full control authority when yaw departure is sensed, can be defeated if the airplane goes into a spin mode in which the yaw rate is relatively low. Although not a departure problem, the F/A-18A has an odd falling leaf spin mode, involving large sideslip, roll rate, and pitch rate oscillations. Response to pitch recovery control is slow. Finally, yaw departures are triggered by pro-spin control applications at medium angles of attack and high subsonic Mach numbers (Figure 9.13).
Boeing F/A-18E/F An automatic spin detection and recovery mode has been added relative to older F/A-18 models. The falling-leaf characteristic of the F/A-18A/C is still present with the bare airframe. However, a new в feedback eliminates the falling-leaf mode (Heller et al., 2001).
Grumman EA-6B This airplane was not included in the AGARD survey paper by Anderson, Enevoldsen, and Nguyen. However, its nose-slice behavior at the stall is documented in AIAA Paper 87-2361 by Frank L. Jordan, David E. Hahne,
Matthew F. Masiello, and William Gato. Approaching the stall, the EA-6B first experiences a rolloff, followed by a nose slice. Numerous EA-6B accidents in fleet service attributed to departures led to a NASA research program on the problem (Chambers, 2000). An EA-6B fitted with NASA modifications (higher vertical tail, inboard wing leading-edge droop, etc.) had departure-free performance, but budgetary constraints prevented their application to service airplanes.
McDonnell Douglas F-15E Thisairplane islikewise not included in the AGARD survey. Its departure characteristics are described in Sitz, Nelson, and Carpenter (1997). Control laws are modified for yaw rates above 42 degrees per second, to increase differential tail power in recovery. Departures are found with lateral loading asymmetry. With the left wing loaded, at angles of attack above 30 degrees, rolls to the right are rapid and hard to counter.
Rockwell/MBB X-31 Departures of this research canard fighter at angles of attack of 60 degrees were corrected by a fuselage nose strake (Chambers, 2000).
The conclusion to be drawn from this survey is that departures can still be obtained on modern fighter airplanes. Designers should concentrate on understanding and controlling the vortex flows that often underlie departures, on simple warning cues and recovery procedures, and on crew restraint systems that permit functioning in the face of strong accelerations.
CHAPTER 10