The F4D Skyray Experience
At the Douglas Aircraft Company’s El Segundo plant the F4D (later F-6) Skyray was being delivered in service test quantities at the height of the inertial coupling excitement. While it was becoming clear that the coupling problem could be eased, if not avoided, by artificial pitch and yaw damping, these devices were still heavy and unreliable. In any case, properly applied, they are placed in series into a control circuit. That is, artificial damping devices are not a parallel installation, as are many automatic pilots, but are an integral part of the control run from stick to control surface. A series-type artificial damping device cannot be easily retrofitted to a production airplane.
|
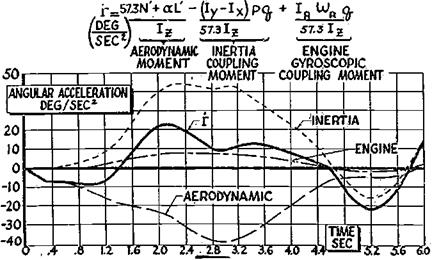
Figure 8.7 The relative importance of aerodynamic, inertial coupling, and engine gyroscopic terms in yawing acceleration during a rapid roll in the North American F-100. In this example, aerodynamic moment is the major factor initially; then inertial coupling overpowers it. (From Wykes, WADC Conf. 56WCLC-1041, 1956) |
High levels of static longitudinal and directional stability were likewise known to be helpful, increasing the roll rates that would cause coupling to occur. In the case of the tailless F4D, high levels of static longitudinal and directional stability could hardly have been designed into the basic airframe, even if the need had been known when the ship was laid out.
The only remaining option for the F4D at that stage was to determine safe maneuver limits, the points at which inertial coupling effects did not cause problems. The airplane could then be restricted by placard, with its pilots depended upon to operate within these limits. The problem of determining F4D safe maneuver operating limits fell into the hands of Robert W. Bratt, who was able to collect the large body of numerical data needed on Douglas Accounting Department digital computers.
The analog computers belonging to the Douglas Flight Controls Department could have in principle run the problem, except for two factors. First, the inertial coupling equations of motion include a large number of mathematical nonlinearities, such as trigonometric functions, needed to resolve gravity along airplane axes, and multiplications, needed to solve the Euler, or moment, equations. But representing nonlinearities on the analog computers of those days was a severe problem. The best analog trigonometric function generators and multipliers were small electromechanical servomechanism devices that were costly and somewhat slow. A few systems boasted “quarter-square” multipliers, which had no moving parts but were inaccurate.
The second drawback to having used analog computers for the F4D inertial coupling problem was that accuracy and repeatability were poor. Bratt’s problem was to cover systematically in small increments all combinations of lateral and longitudinal stick throws, including phasing or sequence between the two, trimmer settings, and airspeeds and altitudes, in order to establish the points of coupling onset. Vacuum-tube analog computers were not only subject to frequent breakdowns, but also to drifts and gain changes that could make a hash out of a systematic study. These considerations led to using the digital computer, an early use for these machines in flight dynamics.