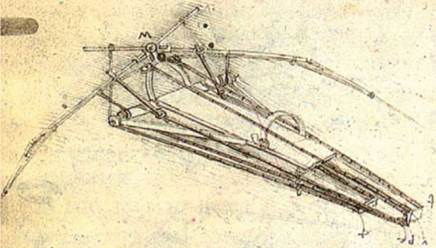
Bird, bat, and insect flight has fascinated humans for many centuries. As enthusiastically observed by Dial [1], most species of animals fly. Based on his acute observation of how birds fly, Leonardo da Vinci conceptualized flying machines, which can be seen in documents such as the Codex on the Flight of Birds, published circa 1505 [2]; some illustrations of his work are shown in Figure 1.1. Otto Lilienthal was among the most dedicated and successful creators of flying machines at the dawn of human flight. He designed and demonstrated many hang gliders (see Fig. 1.2). Unfortunately, Lilienthal lacked sufficient knowledge of the science of flight and was killed in a fatal fall. For those who wish to explore in greater detail the history and the technology of early flight, John Anderson’s Inventing Flight [3] offers interesting and well – documented information. Of course, there are ample records of humankind’s interest in natural flyers from the artistic angle. Figure 1.3 shows four examples: (Figure 1.3a) decorative art done about 2,500 years ago, in China’s Warring Period; (Figure 1.3b) a bronze crane model uncovered from the First Emperor’s grave, who died in 210 BC; a pair of bas-reliefs (Figure 1.3c, d) uncovered from the Assyrian palace in today’s Iraq, dated back to the 8th century BC; (Figure 1.3e) a stone sculpture of a standing owl from the Shang Dynasty, China, created in the 12th century BC or earlier!
There are nearly a million species of flying insects, and of the non-insects, another 13,000 warm-blooded vertebrate species (including mammals, about 9,000 species of birds, and 1,000 species of bats) take to the skies. In their ability to maneuver a body efficiently through space, birds, bats, and insects represent one of nature’s finest locomotion experiments. Although aeronautical technology has advanced rapidly over the past 100 years, nature’s flying machines, which have evolved over 150 million years, are still impressive. Considering that humans move at top speeds of 3-4 body lengths per second, a race horse runs approximately 7 body lengths per second, a cheetah accomplishes 18 body lengths per second [4], and a supersonic aircraft such as the SR-71 “Blackbird” traveling near Mach 3 (~900 m/s) covers about 32 body lengths per second, it is remarkable that a Common Pigeon (Columba livia) frequently attains speeds of 22.4 m/s, which converts to 75 body lengths per second. A European Starling (Sturnus vulgaris) is capable of flying at 120 body lengths per second, and various species of swifts are even faster, flying more than 140 body lengths per second. Whereas the roll rate of highly aerobatic aircraft (e. g., A-4 Skyhawk) is approximately 720°/s, a Barn Swallow (Hirundo rustics) has a roll
|
|
|

|
|

|
|

Figure 1.1. A drawing of a design for a flying machine by Leonardo da Vinci (c. 1488). This machine was an ornithopter, with flapping wings similar to a bird, first presented in his Codex on the Flight of Birds circa 1505 [2].
|
 Figure 1.3. Birds recorded in early human history: (a) design of a wine vessel, early Warring period (475-early fourth century BC), China (Shanghai Museum, Shanghai); (b) a bronze crane-eating fish, uncovered inside the First Emperor’s grave site, Xian, China (Museum of Emperor QinShihuang, Xian); (c, d) Assyrian bas-reliefs, circa eighth century BC (British Museum, London); (e) Stone sculpture of a standing owl, Shang Dynasty, China, around the 12th century BC or earlier (Academia Sinica, Taipei).
Figure 1.3. Birds recorded in early human history: (a) design of a wine vessel, early Warring period (475-early fourth century BC), China (Shanghai Museum, Shanghai); (b) a bronze crane-eating fish, uncovered inside the First Emperor’s grave site, Xian, China (Museum of Emperor QinShihuang, Xian); (c, d) Assyrian bas-reliefs, circa eighth century BC (British Museum, London); (e) Stone sculpture of a standing owl, Shang Dynasty, China, around the 12th century BC or earlier (Academia Sinica, Taipei).
|

Figure 1.4. According to the simplified static aerodynamics, bumblebees were proclaimed to be unfit to fly.
|
rate in excess of 5,000°/s. The maximum positive G-force permitted in most general aviation aircraft is 4-5 G, and select military aircraft withstand 8-10 G. However, many birds routinely experience positive G-forces in excess of 10 G and up to 14 G. Such superior maneuvering and flight characteristics are primarily because of the “scaling laws” with respect to a vehicle’s size, as well as intuitive but highly developed sensing, navigation, and control capabilities. As McMasters and Henderson put it, humans fly commercially or recreationally, but animals fly professionally [5].
Compared to vehicles with flapping wings, conventional airplanes with fixed wings are relatively simple; the forward motion relative to the air causes the wings to generate lift, with the thrust being produced by the engine via either propellers or exhaust gas. However, in biological flight the wings not only move forward relative to the air but they also flap up and down, plunge, and sweep [1] [4] [6]-[8], so that both lift and thrust can be generated and balanced in accordance with the instantaneous flight task. Aymar [9] and Storer [10] provide early photographs and some general observations. Although in the early days of flight studies, much of the analysis of flapping wing aerodynamics was based on an analogy to the fixed-wing counterpart, it was known that this approach encountered qualitative difficulties, especially when the size of a flyer became smaller, as in small birds, small bats, and insect regimes. In 1934, Antoine Magnan, an entomologist, discussed an analysis by Andre Sainte- Lague, an engineer, that whereas the lift generated by wings can adequately support an aircraft to stay aloft, the same is not true at equivalent speeds of a bee [11]. In other words, an airplane the size of a bee, moving as slowly as a bee, should not be able to fly [12]. Yet, of course, bumblebees, shown in Figure 1.4, can fly.
This example illustrates in simple fashion the implied conclusion – that the theory of fixed-wing aerodynamics cannot explain certain critical aspects of
|

Figure 1.5. The instantaneous flapping wing patterns can sometimes look reasonable to be analogous to stationary wings under a series of quasi-statically defined conditions.
|
flapping wing aerodynamics. The aforementioned framework of fixed wings essentially considers flapping wing dynamics as a series of “snapshots” (as illustrated by Fig. 1.5), neglecting the influence of the aerodynamics and wing motion at an earlier moment on the aerodynamics at a later time, based on the so-called quasi-steady approach. In reality, a small flyer can often benefit from manipulating unsteady fluid flows using flapping wing aerodynamics. A rich variety of natural flyers, as depicted in Figure 1.6, can be observed to characterize the instantaneous flapping wing motions. Depending on the real-time flight requirements, these complex motions and wing shapes generate the desirable lift and thrust in different flight environments.
As another example, Franco et al. [13] investigated fluid-structure interactions (FSIs) seen in jellyfish. They reported aperiodic flow despite the relative simplicity of a jellyfish’s body shape and motion, as shown in Figure 1.7. Muscle contraction reduces the volume of the subumbrellar cavity (i. e., the region underneath its umbrella-shaped body), resulting in a net downward flux of fluid. The motion of the lower margin of the bell generates vortex rings of opposite rotational sense during the contraction and relaxation phases of the swimming cycle. Franco et al. [13] observed that these vortices act to entrain fluid from above the animal into the subumbrel – lar cavity, where the feeding and sensory apparatuses of the animal are located. Furthermore, despite the approximate periodicity of the swimming motion, inspection of the flow created by the animal indicates that it is indeed aperiodic in time. Because the animal does not swim at a constant velocity, a periodic flow cannot be constructed by any Galilean transformation of frame. Instantaneous streamlines of the flow field, measured by Franco et al. [13] using digital particle image velocimetry,
|

Figure 1.6. In reality, the instantaneous flapping wing patterns are very complicated. Depending on the real-time flight requirements, necessary lift and thrust are generated by dynamic mechanisms resulting from unsteady wing movement and shape changes.
|
|

Figure 1.7. Dye visualization of jellyfish vortex wake. Time series shows vortices of clockwise and counterclockwise rotation sense generated during the contraction and relaxation phases of the swimming cycle, respectively. Bell diameter is 10 cm. Images from Franco et al. [13].
|
|

Figure 1.8. Instantaneous streamlines of flow around a jellyfish as it swims vertically. Left: End of relaxation phase of swimming cycle. Right: End of contraction phase of swimming cycle. Bell diameter is 10 cm. Images from Franco et al. [13].
|
indicate local entrainment of fluid from above the animal into the subumbrellar cavity during the entire swimming cycle. Simultaneously, as shown in Figure 1.8, a net downward momentum flux propels the animal forward. This study illustrates that (i) the flow field and force generation processes are highly time dependent and cannot be described based on a simple quasi-steady framework without substantial corrections, and that (ii) the movement and shape deformation of the body influence animal locomotion in major ways.
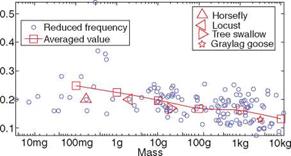
In addition to generating the aerodynamic forces, flapping wings can also significantly enhance the maneuverability of a flyer. Figure 1.9 illustrates several maneuvering characteristics of biological flyers; these capabilities are difficult to mimic by human-made machines. By combining flapping motion, wing deformation, body contour, and tail adjustment, natural flyers can track targets precisely at amazing speeds. Another issue of interest is the weight of the wings relative to the total animal weight. As summarized in Table 1.1, bat wings, depending on the species, are close to 20 percent of the wing-to-total bat weight. The wings of other natural flyers, as shown in Table 1.2, including large birds such as osprey and vultures, account for 20 percent or more of their body weight. Many butterflies (such as Scarce Swallowtail, Large White) also have relatively heavy wings, around 15 to 25 percent of body weight. The wings of a Small Heath, a small, yellow-orange butterfly that flies close to the ground, are about 5 percent of its body weight. Bees, wasps, flies, and the like all have very light wings, typically less than 1 percent of their body weight.
Heavier wings require more energy to flap; nevertheless their larger inertia enables the flyers to make turns within one or two flapping periods. Those with a higher wing-to-body mass ratio and moment of inertia, such as bats and butterflies, are more maneuverable, capable of making abrupt changes of trajectories within a time comparable to that of a flapping cycle. However, they pay a penalty for this ability because a heavier wing consumes more energy while flapping. Many small
|
(a) (b)

Figure 1.9. Maneuvering capabilities of natural flyers: (a) Canadian Geese’s response to wind gust; (b) speed control and target tracking of a seagull; (c) precision touchdown of a finch; (d) a hummingbird defending itself against a bee; (e) the asymmetric movement of wings and tail of a Black Kite while hunting.
|
flyers such as hummingbirds and insects (with many butterflies as a noticeable exception) tend to have much faster flapping time scales than their bodies’ response time scale. For the higher wing-to-body mass ratio group, with the flapping and body response time scales being comparable, the flyer’s flight dynamics and control need to be closely linked to the instantaneous aerodynamics, because the time history of the flapping wing aerodynamics directly affects a flyer’s performance characteristics. For the lower wing-to-body mass ratio group, whose flapping time scales are significantly shorter than their bodies’ response time scale, the lift, drag, and thrust variations during the flapping cycle tend to be smoothed out over the entire flight flapping cycles.
|
Table 1.1. Mass of wing and body, and wing dimensions for eight species of bats. With relatively heavier wings, bats can maneuver and make a turn within a stroke or two. On the other hand, they have to work harder to flap
|
Species
|
mb (kg)
|
mw (kg)
|
mw /mb (%)
|
b (m)
|
|
S (m2)
|
AR (-)
|
W/S
(N/m2)
|
|
Egyptian Fruit Bat
|
8.34 >
|
< 10-2
|
2.06
|
< 10-2
|
24.70
|
5.30 x
|
10-1
|
4.65 x
|
10-2
|
6.4
|
22
|
|
(Rousettus aegyptiacus) Minor Epauletted
|
4.16 >
|
< 10-2
|
8.76
|
<10-3
|
21.03
|
4.00 x
|
10-1
|
2.90 x
|
10-2
|
5.8
|
18
|
|
Fruit Bat
(Epomophorus
anurus)
Common Pipistrelle
|
4.57 >
|
< 10-3
|
7.34
|
<10-4
|
16.08
|
2.09 x
|
10-1
|
6.50 x
|
10-3
|
6.7
|
8.0
|
|
(Pipistrellus pipistrellus) Common Noctule
|
2.35 >
|
< 10-2
|
3.00
|
<10-3
|
12.76
|
3.44 x
|
10-1
|
1.61 x
|
10-2
|
7.4
|
16
|
|
(Nyctalus noctula) Northem Bat
|
8.20 >
|
<10-3
|
1.70
|
<10-3
|
20.73
|
2.77 x
|
10-1
|
1.15 x
|
10-2
|
6.7
|
8.4
|
|
(Eptesicus nilssonii) Particoloured Bat
|
1.24
|
< 10-2
|
1.72
|
<10-3
|
13.87
|
2.98 x
|
10-1
|
1.22 x
|
10-2
|
7.3
|
11
|
|
(Vespertilio
murinus)
Brown Long-Eared
|
7.83
|
<10-3
|
1.17
|
<10-3
|
14.94
|
2.70 x
|
10-1
|
1.23 x
|
10-2
|
5.9
|
7.2
|
|
Bat (Plecotus auritus) Large-Eared
|
3.01
|
< 10-2
|
5.48
|
<10-3
|
18.19
|
4.49 x
|
10-1
|
2.17 x
|
10-2
|
9.3
|
16
|
Free-Tailed Bat
(Otomops
martiensseni)
|
Notes: mb is body mass, mw is wing mass (total), b is wingspan, S is wing area (total), and AR is aspect ratio. Note the body mass is computed by the subtraction of the total wing mass from the total mass.
Source: [47].
However, this feature does not mean that the flapping wing aerodynamics of small flyers can simply be considered as quasi-steady. As is discussed in detail in Chapter 3, the time history of the wing motion is often important to flapping wing aerodynamics. Figure 1.10 shows hummingbirds conducting highly difficult and precise flight control. As illustrated in Figure 1.11, in which several photos highlight the flapping pattern along with a flow field illustration from Warrick et al. [14], hummingbird wing motion exhibits a figure-eight pattern and is highly adaptive to accommodate the challenges posed by wind gust, target tracking, and mitigation of potential interference and threat.
Natural flyers synchronize their wings, body, legs, and tail to perform many tasks. As shown in Figure 1.12, they can take off on water, from land, and off a tree, exhibiting varied and sophisticated patterns. While gliding, as shown in Figure 1.13, they flex their wings to control their speed and direction. On landing, as depicted in Figure 1.14, birds use wing-tail combinations to correct flight trajectory and to adjust for the location of the available landing area. If they need to slow down and adjust the detailed flight trajectory, they fully expand their wings to increase drag and reduce speed; otherwise, they simply fold their wings to reduce lift without slowing down.
|
Table 1.2. Mass of wing and body, and wing dimensions for some insects [48] and birds [49]. With lighter wings, which results in time scale differences between the wing movement and the body movement, flyers such as bumblebees need to flap a number of times before being able to make turns
|
Flyers/Species
|
mb (kg)
|
mw (kg)
|
mJmb (%)
|
R (m)
|
S(m2)
|
|
AR
|
W/S (N/m2)
|
|
Birds
|
|
Griffon Vulture (Gyps fulvus)
|
7.27:
|
x 100
|
1.60 x
|
<10-3
|
22.00
|
6.98
|
x 10-1
|
1.05 x
|
100
|
1.85
|
67.59
|
|
Osprey (Pandion haliaetus)
|
1.11:
|
x 100
|
3.10 >
|
<10-1
|
28.05
|
4.96
|
x 10-1
|
2.92 x
|
10-1
|
3.37
|
37.07
|
|
Pallid Harrier (Circus macrourus)
|
3.86:
|
x 10-1
|
7.51 x
|
<10-2
|
19.46
|
3.57
|
x 10-1
|
1.41 x
|
10-1
|
3.61
|
26.77
|
|
Hummingbrid (Lampornis clemenciae)
|
8.4 x
|
10-3
|
6.00 x
|
<10-4
|
7.14
|
8.5 x
|
10-2
|
3.50 x
|
10-3
|
8.26
|
25.2
|
|
Insects
Giant Peacock Moth (Saurnia pyri)
|
1.89:
|
x 10-3
|
3.00 x
|
<10-4
|
15.87
|
7.00
|
x 10-2
|
1.20 x
|
10-2
|
1.85
|
1.54
|
|
Butterflies
|
|
Scarce Swallowtail (Papilio podalirius)
|
3.00:
|
x 10-4
|
8.00 x
|
<10-5
|
26.67
|
3.70
|
x 10-2
|
3.60 x
|
10-3
|
1.52
|
0.82
|
|
Large White (Pieris brassicae)
|
1.27:
|
x 10-4
|
2.10 x
|
<10-5
|
16.54
|
3.10
|
x 10-2
|
1.84 x
|
10-3
|
2.09
|
0.68
|
|
Small Heath (Coenonympha pamphilus)
|
4.60:
|
x 10-5
|
3.50 x
|
<10-6
|
7.61
|
1.61
|
x 10-2
|
4.80 x
|
10-4
|
2.13
|
0.94
|
|
Moths, Bees, and Other Insects
Death’s-Head Hawkmoth (Acheronia atropos)
|
1.60:
|
x 10-3
|
6.70 x
|
<10-5
|
4.19
|
5.10
|
x 10-2
|
2.05 x
|
10-3
|
5.08
|
7.65
|
|
Hummingbird Hawkmoth (Macroglossum stellatarum L.)
|
2.82
|
x 10-4
|
9.18 x
|
<10-6
|
3.26
|
2.13
|
x 10-2
|
3.79 x
|
10-4
|
4.79
|
7.29
|
|
Hawkmoth (Manduca sexta)
|
1.60:
|
x 10-3
|
9.00 x
|
<10-5
|
5.63
|
4.85
|
x 10-2
|
1.80 x
|
10-3
|
5.23
|
9.20
|
|
German Wasp (Vespula germanica F.)
|
2.40
|
x 10-4
|
1.39 x
|
<10-6
|
0.58
|
1.62
|
x 10-2
|
1.33 x
|
10-4
|
7.89
|
17.68
|
|
European Hornet (Vespa crabro L.)
|
5.97:
|
x 10-4
|
5.68 x
|
<10-6
|
0.95
|
2.43
|
x 10-2
|
3.04 x
|
10-4
|
6.08
|
19.25
|
|
European Hoverfly (Eristalis tenax)
|
1.29:
|
x 10-4
|
1.13 x
|
<10-6
|
0.88
|
1.27
|
x 10-2
|
8.26 x
|
10-5
|
7.78
|
15.31
|
|
Honeybee (Apis mellifica L.)
|
9.75
|
x 10-5
|
4.25 x
|
<10-7
|
0.44
|
9.95
|
x 10-3
|
5.98 x
|
10-5
|
6.62
|
15.98
|
|
Red-Tailed Bumblebee (Bombus lapidaries)
|
4.95:
|
x 10-4
|
3.10 x
|
<10-6
|
0.63
|
1.65
|
x 10-2
|
1.65 x
|
10-4
|
6.60
|
29.40
|
|
Buff-Tailed Bumblebee (Bombus terrestris)
|
3.88:
|
x 10-4
|
2.50 x
|
<10-6
|
0.64
|
1.60
|
x 10-2
|
1.42 x
|
10-4
|
7.21
|
26.78
|
|
Blue Fly (Caliphora erythorocephala)
|
6.10:
|
x 10-5
|
5.27 x
|
<10-7
|
0.86
|
1.04
|
x 10-2
|
6.33 x
|
10-5
|
6.83
|
9.44
|
Source: Insects [48] and birds [49].
|
|

Figure 1.10. Natural flyers can track a target precisely and instantaneously. Shown here are hummingbirds using flapping wings, contoured body, and tail adjustment to conduct flight control.
|
Since the late 1990s, micro air vehicles (MAVs) have attracted substantial and growing interest in the engineering and science community. An MAV is defined as a vehicle with a maximal dimension of 15 cm or less, which is comparable to the size of small birds or bats, and with a flight speed of 10-20 m/s [15]. Equipped with a video camera or a sensor, MAVs can perform surveillance and reconnaissance, targeting, and biochemical sensing at remote or otherwise hazardous locations. With the rapid progress made in structural and material technologies, miniaturization of power plants, communication, visualization, and control devices, numerous groups have developed successful MAVs. In the process, many MAV concepts, based on the fixed wing, rotary wing, and flapping wing, have been investigated [16]. Figure 1.15a shows an inventive 15-cm MAV design by Ifju et al. [17] that uses a fixed, flexible wing concept. Figure 1.15b shows a rotary wing MAV with 8.5-cm rotary diameter designed by Muren (http://www. proxflyer. com). Figure 1.15c shows a biplane MAV designed by Jones and Platzer [18], which uses a hybrid flapping-fixed-wing design, with the flapping wing generating thrust and the fixed wing producing necessary lift. Figure 1.15d shows an MAV by Kawamura et al. [19] that relies on a flapping wing to generate both lift and thrust and possesses some flight control capabilities. Figure 1.15e shows a 16.5-cm MAV recently developed by AeroVironment (http://www. avinc. com/), which uses a hummingbird-like flapping wing design. It can hover for eight minutes without external power, fly forward with a speed of 4.9 m/s, return to hover, and then withstand a 2 m/s wind gust from the side without drifting more than 1 meter. Figure 1.15f shows a recently developed 10-cm and 3- gram flapping wing MAV (http://www. delfly. nl/?site=diii&menu=home&lang=en). It can carry a small camera and 1-gram battery and fly up to 5 m/s for 3 minutes. As
|

Figure 1.11. Flapping pattern and flow field of a hummingbird. Agile maneuvering in varied and uncertain environments is critical. The bottom image is from Warrick et al. [14].
|
|
|

Figure 1.12. During takeoff, natural flyers display larger flapping amplitudes, wider and larger wing and tail surfaces, and springing. The level of coordination between wing, tail, and body is remarkable.
|
|

Figure 1.13. Birds such as seagulls glide while flexing their wings to adjust their speed as well as to control their direction.
|
|

Figure 1.14. While landing, birds use various options. They may fold their wings to reduce the lift if the flight speed is appropriate and there are no environmental disturbances such as wind gust. They also often deliberately stall their fully stretched wings on final approach, maximizing drag to obtain quick deceleration and not being concerned about lift during the final stage of flight.
|
demonstrated by the U. S. Defense Advanced Research Projects Agency (DARPA), there is substantial interest in developing and using MAVs with robust “perch and stare” capabilities that can take off without external assistance. There are a number of possible candidates, including the aforementioned flapping-wing-based vehicles and rotorcraft such as quad-rotors [20].
Figure 1.16 highlights detailed vehicle characteristics of flexible wing MAVs designed by Ifju and co-workers. The various international MAV competition venues, initiated by the University of Florida and now widespread globally, have substantially encouraged the development of MAVs. The MAVs operate in the low
 (e)
(e)
Figure 1.15. Representative MAVs: (a) flexible fixed wing [17]; (b) small-sized rotary wing (http://www. proxflyer. com); (c) hybrid flapping-fixed wing, with the fixed wing used for lift and the flapping wing for thrust [18]; (d) flapping wing for both lift and thrust [19]; (e) hummingbird-inspired robotic Nano Air Vehicle (http://www. avinc. com/); and (f) a 5-cm wingspan flapping wing MAV (http://www. delfly. nl/?site=diii&menu=home&lang=en).
Reynolds number (characterizing the relative importance between inertia and viscous effects of the fluid) and, compared to large manned flight vehicles, experience unfavorable aerodynamic characteristics, such as low lift-to-drag ratio [21]. However, the MAVs’ small geometric dimensions result in favorable scaling characteristics, such as reduced stall speed and better structural survivability.
General references offering broad accounts of biological flight, including geometric scaling laws, power, and morphology, as well as simplified modeling, can be found in Alexander [22] [23], Azuma [24], Biewener [25], Brodsky [26], Dudley [27], Grodnitsky [28], Norberg [4], Tennekes [29], Videler et al. [30], Vogel [31],
|

(а) (Ъ)
Figure 1.16. The flexible-wing MAVs (a) can benefit from passive shape adaptation in accordance with instantaneous aerodynamic loading and (b) can be packed very easily based on need. (Courtesy Peter Ifju).
|
Ward-Smith [32], Dalton [33], Pringle [34], Henderson [35], and Floreano et al. [36]. The symposia volumes edited by Wu et al. [37], Pedley [38], and Maddock et al. [39] offer multiple aspects of biological flight as well as swimming. Lighthill [40], Wu [41], Childress [42], and Maxworthy [43] discuss swimming and flying primarily from analytical viewpoints with simplified problem definitions. Finally, the standard texts by Anderson [44], Katz and Plotkin [45], and Shevell [46] present basic knowledge of human-made aerodynamics relevant to both biological and human – made MAVs.
In the following chapters, we offer an introductory and simplified, concept – based framework on the lift – and thrust-generation mechanisms of flapping wing vehicles. Specifically, we present the scaling laws related to the mechanics and energetics of avian flight. Then, we use simple mechanics to describe gliding, forward, and hovering flight, as well as drag and power related to avian flight. The different power components are first presented separately and then summed together, giving the total power required for hovering and forward flight. The results of these different power calculations can be summarized in the form of power curves. The analyses are based on the quasi-steady approach, neglecting the time history of the wing motion. This approach, although incomplete in certain important aspects (such as coupled and multi-scale mechanics between wing and fluid and between wing and body and tail, shape deformation, and the time history of force generation), can offer useful insights into some of the important and basic issues related to flapping wing flight. More detailed and critical discussions accounting for unsteady fluid physics and fluid-structure interactions are presented in later chapters.
![]()
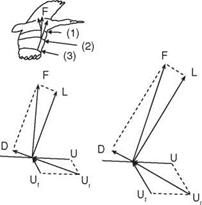
 (to reduce drag); when this occurs only the arm wing contributes to aerodynamic lift during the upstroke.
(to reduce drag); when this occurs only the arm wing contributes to aerodynamic lift during the upstroke.![]()
![]()
![]()
![]()
![]() obtained at each wing section throughout the wing stroke. Since the relative velocity determines the direction of the resultant aerodynamic force, this force is directed backward at the wing root and gradually turned forward when moving along the wingspan. At the wingtip region, the resultant aerodynamic force points toward the forward direction, giving both lift and thrust.
obtained at each wing section throughout the wing stroke. Since the relative velocity determines the direction of the resultant aerodynamic force, this force is directed backward at the wing root and gradually turned forward when moving along the wingspan. At the wingtip region, the resultant aerodynamic force points toward the forward direction, giving both lift and thrust.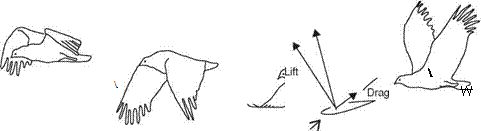











![Подпись: Figure 1.23. Wingtip paths relative to the body for a variety of flyers, as indicated by arrows. (a) albatross, fast gait; (b) pigeon, slow gait; (c) horseshoe bat, fast flight; (d) horseshoe bat, slow gait; (e) blow fly; (f) locust; (g) June Beetle; (h) fruit fly. From Alexander [22].](/img/3131/image043_4.gif)
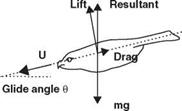 Albatross, with a wing span more than 3 m, has a reported lift-to-drag ratio of 19, whereas the fruit fly, which has a span of 6 mm, has a ratio of 1.8 [22]. If the animal has a low lift-to-drag ratio, it must glide (if it can) with a considerable increase in glide angle. For example, a lizard (the genus Draco) from Southeast Asia has a lift – to-drag ratio of 1.7 and glides at an angle of 30°, whereas a North American flying squirrel glides at the angle of about 18° to 26° with a lift-to-drag ratio of 2 or 3 [22].
Albatross, with a wing span more than 3 m, has a reported lift-to-drag ratio of 19, whereas the fruit fly, which has a span of 6 mm, has a ratio of 1.8 [22]. If the animal has a low lift-to-drag ratio, it must glide (if it can) with a considerable increase in glide angle. For example, a lizard (the genus Draco) from Southeast Asia has a lift – to-drag ratio of 1.7 and glides at an angle of 30°, whereas a North American flying squirrel glides at the angle of about 18° to 26° with a lift-to-drag ratio of 2 or 3 [22].

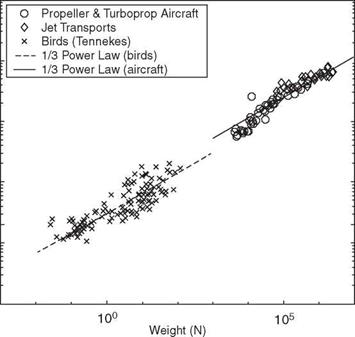
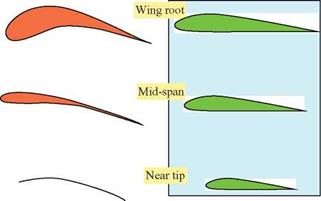
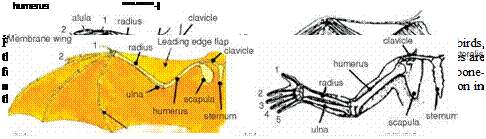





 Figure 1.3. Birds recorded in early human history: (a) design of a wine vessel, early Warring period (475-early fourth century BC), China (Shanghai Museum, Shanghai); (b) a bronze crane-eating fish, uncovered inside the First Emperor’s grave site, Xian, China (Museum of Emperor QinShihuang, Xian); (c, d) Assyrian bas-reliefs, circa eighth century BC (British Museum, London); (e) Stone sculpture of a standing owl, Shang Dynasty, China, around the 12th century BC or earlier (Academia Sinica, Taipei).
Figure 1.3. Birds recorded in early human history: (a) design of a wine vessel, early Warring period (475-early fourth century BC), China (Shanghai Museum, Shanghai); (b) a bronze crane-eating fish, uncovered inside the First Emperor’s grave site, Xian, China (Museum of Emperor QinShihuang, Xian); (c, d) Assyrian bas-reliefs, circa eighth century BC (British Museum, London); (e) Stone sculpture of a standing owl, Shang Dynasty, China, around the 12th century BC or earlier (Academia Sinica, Taipei).










 (e)
(e)