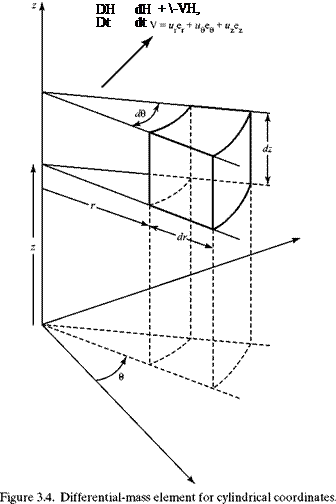
Angular Velocity and Strain
In general, as a fluid particle moves from point to point in a flow field, it rotates and its shape is distorted (i. e., strain). In this section, the rotation or angular velocity of a moving fluid particle is defined in terms of derivatives of the velocity components of the particle. Any deformation of the particle shape is due to viscous-shear effects, which are absent in the perfect-fluid model considered in this chapter. An expression for strain is needed later in the development of the viscous-flow terms in the conservation equations (see Chapter 8) and is easily obtained simultaneously with the rotation effects. Hence, the strain terms are derived here and then set aside for later use.
Rotation is defined as a property of the fluid particle and not of the global flow field. Thus, for example, a flow field with circular streamlines under certain circumstances might have zero rotation if individual particles move along the streamlines without spin. In considering the rotation of a solid body (e. g., a spinning flywheel), it is sufficient to determine angular velocity simply by making a straight line on the flywheel and a reference line on a fixed surface. The time rate of change of the angle made by the line marked on the wheel with respect to the fixed reference line is the angular velocity of the flywheel.
A more general definition is necessary for a moving fluid particle because it can deform. Of course, the general definition of rotation for a fluid particle when
 |
|
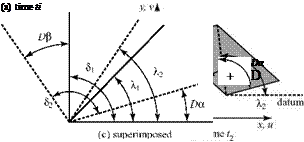
applied to a solid-body rotation problem must produce the familiar answer. Consider a moving fluid particle of infinitesimal size in a two-dimensional flow in the (x, y) plane at an arbitrary initial time t1. For example, assume that at time t1, the particle is a rectangle. The assumption of a rectangular shape is, of course, not a requirement; use of a more general shape leads to the same results. Now, imagine that the molecules making up the straight edges of the particle are painted and that a straight diagonal is drawn between two corners of the rectangle (Fig. 4.1(a)).
Take a snapshot of this particle and, on the photographic negative, define the angle 51 as the included angle in the corner (here, 90°) and the angle X to be the angle that the diagonal makes with a horizontal datum parallel to the x-axis. Now, imagine that the fluid particle moves and distorts and that a second snapshot is taken at a later time, t2 (Fig. 4.1(b)). Although the particle distorts, the lines defining the angles still may be considered straight because the element is infinitesimally small. Next, mark each negative with a dot at the lower left corner of the fluid particle, superpose the two negatives, and put a pin through the dots (Fig. 4.1(c)). Such a superposition eliminates the translation of the particle between snapshots.
Now define:
DX
1. rotation or angular velocity =
„ D5 Dt
2. strain = Dt = _£xy
Notice that the time rates of change of the angles are written with an uppercase D because these are rates of change with respect to a moving fluid particle. The subscript xy indicates that this is the strain in the x-y plane, and the subscript z indicates that this is rotation in a plane perpendicular to the z-axis. These subscripts are necessary because two other planes in three-space could be drawn and other appropriate expressions defined.
Figure 4.1 shows that:
1 П 1
X, = -5, = — and X2 =Da +—52 =Da + — — + Dp-Da I. 1 2 1 4 2 2 2 21 2 F 1
Thus, rotation wz is given by:
|
|
||
|
|||
|
|||
![]() DX. 1
DX. 1
— = w z = rotation = –
Dt z 2
Similarly, 5, = — and 52 = — + Dp – Da. Thus:
|
|
|
|
|
|
D5 Dp Da t. Da Dp
— = ———– = strain =—————– .
Dt Dt Dt xy Dt Dt
At first glance, it appears that not much was accomplished because rotation and strain were expressed in terms of other variables and in a more complicated way. However, these formulations allow rotation and strain to be expressed in terms of velocity-component derivatives.
Next, recast Fig. 4.1(c) as Fig. 4.2 and recognize why the angles Da and Dp are generated. It is because the “painted” molecules that comprise the edges of the fluid particle are moving with increasing speed in both the x – and y-directions the farther the molecule is located from the corner. (Recall that the gross translation components u and v of the particle were eliminated in the superposition in Fig. 4.1(c).)
Because Fig. 4.2 describes the limit as Dt ^ Q, the paths of the painted molecules may be represented accurately as straight lines even though they are actually circular arcs. In this short time interval, assume that the molecule farthest from the center along the x-axis has moved a distance h. Then, with the tangent of the angle being equal to the angle itself for a small angle:
|
|
|
|
|
|
![]()
De_-d£. (4.1b)
Dt dy
Note from Fig. 4.1(c) that an arbitrary counterclockwise positive sign was given to Da and Dp. Because Fig. 4.2 indicates that Dp/Dt is positive but that the rate of change of и with respect to y is negative, a compensating minus sign must be inserted into Eq. 4.1b, as shown.
Finally, substituting Eq. 4.1 into the definitions of rotation and strain, the desired result is obtained—namely, that these definitions are expressed now in terms of definable and measurable local properties of the flow field. Thus, the rotation in the x-y plane is given by:
Substituting Eq. 4.1 into the definition for strain yields:
Expressions similar to Eq. 4.3 likewise can be derived for exz and eyz. The concept of strain is discussed in more detail and applied in Chapter 8. Eq. 4.3 is not needed at this time.
Analogous expressions for rotation rax and юу can be derived similarly in the other two orthogonal planes. These three expressions for rotation represent the components of the angular velocity of a fluid particle in three-space and may be thought of as the three components of an angular velocity vector. Thus,
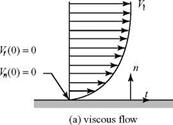
A flow is said to be irrotational if the magnitude of this angular velocity vector is identically zero; that is, all three components of the rotation vector are zero. Flows that are irrotational are demonstrated as far simpler to analyze than those that are not. It might seem that irrotational flows would be such special cases as to be of little practical importance. If we consider the velocity profile within a boundary layer in two dimensions (cf. Fig 2.3, where du/dy >> dv/dx) or realize that the large shearing action within the boundary layer causes the fluid particles present there to “spin,” then it is clear that a viscous boundary layer is a region of rotational flow. However, it happens that outside the thin boundary layer on a body, the flow can be
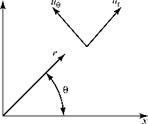
Figure 4.3. Polar-coordinate notation.
 irrotational; hence, inviscid flow is irrotational. An exception occurs when entropy gradients may be present, such as behind a curved shock wave in a supersonic flow. Of course, the entire flow field near the body can be rotational if there is a source of vorticity that causes the flow field to be rotational far upstream. The word vorticity is used often instead of rotation; it differs by only a factor of two, as discussed in the next subsection.
irrotational; hence, inviscid flow is irrotational. An exception occurs when entropy gradients may be present, such as behind a curved shock wave in a supersonic flow. Of course, the entire flow field near the body can be rotational if there is a source of vorticity that causes the flow field to be rotational far upstream. The word vorticity is used often instead of rotation; it differs by only a factor of two, as discussed in the next subsection.
The expression for angular velocity can be written readily in polar coordinates. Such coordinates are frequently of great value in analyzing flow fields, especially those involving curved streamlines. A detailed list of the fundamental fluid equations in various coordinate systems is included in the appendixes. The two velocity-vector components at a point in a polar-coordinate frame are shown in Fig. 4.3.
In polar coordinates (Fig. 4.3), the angular velocity expression is:
|
|
||
|
|||
|
|||
|
|||
|
|||
![]()
In this derivation, both sides of the benchmark fluid particle considered in Fig. 4.1 are assumed to rotate with time in a counterclockwise direction. The student should verify that the same results for ю and exy are obtained if the rotations of both sides are assumed to be clockwise or if one is taken to be clockwise and the other counterclockwise.
example 4.3 Given: A physically possible flow field is steady, incompressible, and two-dimensional and it has circular streamlines; it is also irrotational.
Required: Determine the behavior of the tangential velocity component of this flow field.
Approach: Because the flow field is physically possible, continuity must be satisfied. Thus, Eq. 3.52 is needed, as well as the irrotationality condition that ю = 0 in Eq. 4.5.
Solution: If the flow has circular streamlines, it follows that ur = 0 and that uB = Krn, where K is a constant and exponent n is to be determined. Next, write the vector continuity equation (Eq. 3.52) in polar-coordinate form:
![]() dur 1
dur 1
dr r
Then, substitute these expressions for the velocity components ur and ue into
the continuity equation. This leads to the requirement that — (Krn) = 0, which
оЄ
is true for any value of the exponent n. Thus, the use of the continuity equation
did not determine n; any value leads to a physically real flow.
In addition, we required that the flow must be irrotational, meaning that Eq. 4.4 must apply with raz= 0. Substituting the expressions for ur and ue into Eq. 4.4 and performing the differentiation, irrotationality demands that
nKr n-1 + Kr n-1 = 0 = rn-1K(n + 1).
This states that if n = -1, the flow field is irrotational but that the expression for the rotation, raz, is indeterminate at the origin (r = 0). Thus, the flow field described by ur = 0 and ue = K/r satisfies continuity and is irrotational everywhere except at the origin. To settle the question of what happens at the origin requires the development of additional building blocks (see Section 4.6). An irrotational flow with circular streamlines is an important special case called a vortex.
Appraisal: This flow has circular streamlines, yet the fluid particles in the flow exhibit zero rotation. The fluid particles are behaving like the seats on a Ferris wheel in that the angle between a horizontal datum and the diagonal in Fig. 4.1 does not vary with time. If the flow field had circular streamlines and was exhibiting solid-body rotation—as if it were instantaneously frozen and rotating like a wheel—then ue = Kr and Eq. 4.5 yields ю = K. This simply states that the general angular velocity expression, Eq. 4.4, gives the expected answer for a simpler and more familiar special case.











 both sides: u21 1 + xI y
both sides: u21 1 + xI y

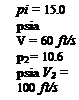
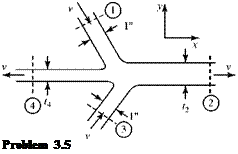
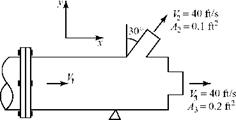
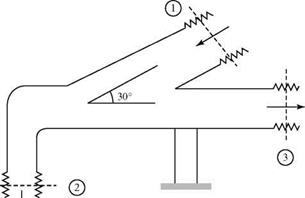 Pamb = 2,000 Psfa Pi = 3,000 psfa p2 = 2,100 psfa p3 = 1,000 psfa
Pamb = 2,000 Psfa Pi = 3,000 psfa p2 = 2,100 psfa p3 = 1,000 psfa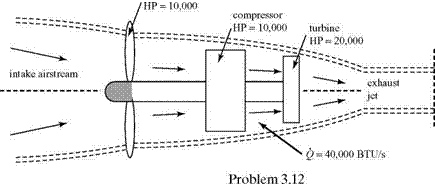
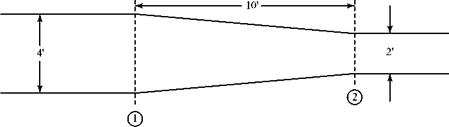
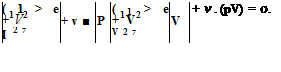

 Steady, adiabatic, inviscid flow
Steady, adiabatic, inviscid flow