Category BASIC AERODYNAMICS

It may be that compressible processes must be tested for reversibility by means of the Second Law of Thermodynamics. For completeness, we show this here in the form of the entropy-rate inequality. In differential form, the Second Law of Thermo­dynamics is:

dS, (3.11)

where S is the system entropy and T is the (absolute) temperature. S can be written in terms of the corresponding intensive property, s (entropy per unit mass) as:

S = J s dm = JJJ psdV.

system

volume

Then, the required rate equation form for the Second Law of Thermodynamics is:

— > Q (3.13)

dt T

Additional Physical Laws

The “laws” describing the physics of fluid motion in rate form usually must be supple­mented by additional information so that a complete mathematical representation is achieved. Important supplementary physical relationships may come from thermo­dynamics, chemistry, heat transfer, or additional mechanical models to fully describe the fluid medium. For example, in Chapter 2, supplementary physical relationships are introduced in the form of the equation of state (see Eq. 2.1) and Newton’s Law of Viscosity (Eq. 2.4). These laws are incorporated as needed to fully describe any given situation.

A fundamental law describes changes of the energy of a system by interaction with its surroundings. The First Law of Thermodynamics is often written in differential form in the notation of thermodynamics as:

dE = 5Q – Ш, (3.7)

where dE is the change in system energy and 5Q and 5W represent the differential flow of heat energy to and differential work done by the system. In some textbooks, the work is defined as that done on the system by the surroundings. Then, the sign on 5W is reversed. We use the more common engineering form expressed in Eq. 3.7. In rate form, the First Law of Thermodynamics may be written as:

(3.10)

where e is the internal energy due to random molecular motion at any point within the system and V 2/2 is the kinetic energy per unit mass. An additional term is often added to this expression to account for the potential energy due to position in a gravity field. This normally is not needed in the gas flows of interest in this book. It could be important in flows of liquid involving large elevation changes.

These important laws of nature specify how the system of particles moves in res­ponse to external forces or moments. For the system (described in an inertial frame of reference), we write:

dP = F

dt

dH

dt

where P and H are the linear and angular momenta of the system, respectively, and F and M are the externally applied sums of forces and moments. Because we are dealing with a system of individual particles, the force F must include the interaction forces between the particles that constitute the system. These occur in equal and opposite pairs, so that it is usually the case that only the forces acting on the boundary of the system must be considered. It may be helpful to review the treatment of systems of particles in textbooks on dynamics.

Remember that the coordinate system in which the momentum vectors, P and H, are expressed must be a Newtonian or inertial coordinate frame; that is, it cannot be accelerating or rotating. If it is necessary or convenient to use noninertial coordi­nates in describing the system motion, then it is necessary to introduce corrective terms (e. g., centripetal and Coriolis effects) into Eqs. 3.3-3.4. This normally is not required in the applications considered in this book because the emphasis is on steady flow without spin.

The linear and angular momentum for the system can be written as integrals over the mass or volume of the system as follows:

P= J V dm = JJJ pV dV (3.5)

system system

mass volume

1 /V

H= J r x V dm= JJJ p(r x V)dV, (3.6)

system system

mass volume

where V is the velocity vector at a point in the system glob and r locates the corre­sponding point in the inertial coordinate system.

Although both linear motion of the system as expressed by the linear momentum P and rotational motion expressed by the angular momentum H are defined here for completeness, only the former appears in most aerodynamics applications. Thus, we carry out further manipulation of Newton’s laws in detail only for the linear momentum changes of the system. The student should notice that completely analogous developments can be made for the angular momentum if needed in a particular application of interest, where angular motion or spin is an important feature.

If the mass of the system is m at the initial instant of time, then its mass is preserved for all time afterward unless there is a process involving this group of particles that changes part of its mass into energy. This could happen if, for instance, nuclear pro­cesses occur in which mass is converted to energy. We do not consider such processes in this book; so, for all cases of interest, we can state with confidence that the mass remains constant. Thus, in rate form, we write:

for the specified system of fluid particles. The mass can be expressed conveniently as an integral over the volume containing only the identified particles:

m= J dm = JJJ pdV, (3.2)

system system

mass volume

where system mass is always meant to identify the mass of the particular glob of par­ticles constituting the defined system; and system volume, V, is that volume of space enclosing the system glob at any given instant of time. Notice that the system volume might be required to change with time (although the mass remains constant) if the density of the glob, p, changes from point to point in the flow field. If Eq. 3.1 is satis­fied, we ensured that system mass is not created or destroyed; in other words, mass is conserved. All other required laws of motion are expressed in similar rate form in the following subsections.

Throughout the discussions in this chapter, we use the simplifications available by application of the modeling ideas discussed in Chapter 2. Thus, the medium is taken to be composed of a continuum of contiguous fluid particles rather than individual molecules. Because we are interested in the dynamics of fluid flow, it is natural to express each physical law describing the motion of these particles as a rate of change of a physical variable required to characterize the material. As examples, we may be interested in the rate at which mass flows across a cross section of a duct, how fluid particles are accelerated by external forces, and the rate at which work is done on the fluid by pressure forces.

All of the physical effects needed in representing the fluid motion can be given in rate form for a system of particles. To aid in visualization of what we are modeling, consider a flow of fluid in which we identify at some arbitrary initial time a distinct “glob” of air consisting of many individual particles. Imagine that the glob can be marked by coloring it with dye. Then, as it moves downstream, it is stretched and deformed by its interaction with the surroundings and by forces acting among the constituent particles. The identity is preserved although its shape, size, and other characteristics may be altered by the motion, by forces applied at its boundaries, or by body forces (e. g., gravity or magnetic force) that act on the entire system, or by energy flowing into or out of the surroundings. Henceforth, we refer to this marked glob as the system.

Each of the required physical laws is expressed in system form. These should be already familiar to students from the study of basic physics and thermodynamics.

The equations for mathematical representation of a moving fluid are derived here for the most general case of an unsteady, compressible, viscous flow. It is most often the case that full generality is not required in a particular application. It may not be

necessary to account for compressibility effects in the flow over an airplane if the speed of flight is sufficiently low. Similarly, viscous forces may be negligible in some applications. An important skill emphasized in this chapter is the decision-making process used to reduce the general formulation to a simpler one that accounts for only the needed physical effects. In the examples mentioned, the density can be held constant if the flow is incompressible or the viscous terms can be dropped when fric­tional effects are not crucial. Such considerations may result in vast simplification of the mathematical problem.

The approach to be followed is illustrated in Fig. 3.1. We start by briefly reviewing the basic physical laws pertaining to conservation of mass, momentum, and energy. These are naturally expressed in familiar form by representing the behavior of a well-defined system of fluid particles. In this Lagrangian form, the equations are of limited use in handling the problems we address. What usually is needed is the effect of the motion of these particles on the forces of interaction on a body immersed in the flow. It is not required to determine a detailed history of the motion of the original group of fluid particles (i. e., the system) as it moves downstream. The Eul – erian control-volume approach as introduced in Chapter 2 provides a powerful tool for determining the properties of the fluid flow at any time and any location in the domain of interest. Review the definitions in Chapter 2 to understand the distinction between a Lagrangian and a Eulerian approach.

As indicated in Fig. 3.1, the first step is to translate the physical laws into control-volume form. The Reynolds’ Transport Theorem provides the mechanism for passing from the Lagrangian-system model to the more convenient Eulerian control-volume representation. The result is a set of integral equations that pro­vide a useful way to describe the effects of fluid motion without knowledge of the details at each point in the region of interest. In other words, it gives an average or overall picture of the motion. There is a significant benefit here because the control volume can be defined in a variety of useful ways to fit the geometry of any par­ticular problem. The shape and location of the boundaries of the control volume can be chosen to accommodate the required size and shape of the problem domain. A control volume can translate, accelerate, or rotate as necessary to fit the definition of the application. Any number of control volumes can be applied in a given problem to provide information about specific parts of the flow field.

Although in most applications we apply directly the differential equations of fluid motion in solving aerodynamics problems in later chapters, there are many useful and practical benefits of the intermediate control-volume integral formula­tion. The control-volume point of view often is a valuable tool in gaining physical understanding in a given situation before undertaking to solve the applicable dif­ferential equations. For example, if we need to determine only the total force acting on an object immersed in a flow, then this information frequently can be found without establishing all the details of the local-gas motion. If, however, we need to know how the fluid-interaction force elements that lead to this net force are distributed over the body, then a “sharper” representation is needed in which the local behavior of the fluid is determined. In this example, it may be necessary to find the actual distribution of pressure and viscous-shear forces over the body sur­face. This can be done only if we pass from the control-volume integral equation form to differential equation form so that we can study how the fluid properties change locally from point to point. Again, Fig. 3.1 illustrates the “plan of attack.” We use the integral control-volume equations to determine the underlying dif­ferential equations. As these analytical steps are carried out in this chapter, it is important to follow the procedure focusing mainly on the reduction from the gen­eral form to specific applications. The final result is a set of mathematical tools that enables the eventual solution of any fluid-dynamics problem. The remainder of the book is devoted to the application of these tools to analyze a wide variety of aerodynamics problems.

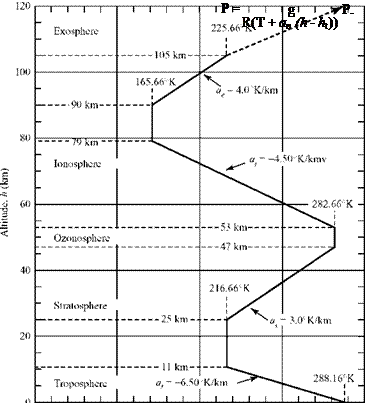
In an isothermal layer, the temperature is constant; therefore, the equation of state reduces to a relationship between pressure and density:

Thus, substituting for the density, the hydrostatics equation becomes:

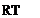
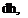dp p

where the combination in parentheses can be considered constant. This simple dif­ferential equation can be solved by direct integration, with the result:

where C2 is a constant of integration that can be evaluated by inserting the initial conditions for a particular isothermal layer from the information in Fig. 2.8 and
from results of the previous gradient layer evaluated at the initial altitude of the isothermal layer. Knowledge of the temperature allows evaluation of the speed of sound and the viscosity coefficients.

The Web site that accompanies this book includes a program labeled STDATM that evaluates the equations described in the preceding paragraphs to give atmos­pheric properties at any altitude. Running the program, the user is asked to choose the system of units (i. e., either English or SI) and to insert the altitude either in meters or feet. The program then returns the corresponding temperature, pressure, density, speed of sound, dynamic-viscosity, and kinematic-viscosity values. Also, the program can be called from within other program modules (described later) to determine automatically the required atmospheric data.

2.3 Summary

This chapter is a review of mathematical concepts for modeling fluid flows such as those experienced in most aerodynamics applications. Important ideas from con­tinuum mechanics and thermodynamics are reviewed, and modeling of the earth’s atmosphere is described using a simple application of fluid statics.

The most important part of this chapter is the introduction of the powerful method of dimensional analysis and the associated ideas of similarity. Application of these ideas reduces the basic problem of aerodynamics—namely, the estimation of the principal aerodynamic forces and moments—to its simplest form. We found that the key to solving this problem is the estimation of dimensionless coefficients such as lift and drag coefficients. An important discovery is that these coefficients are dependent on basic similarity parameters that can be identified as ratios of the fundamental set of forces that characterize the gas motion. In aerodynamics, by far the most important similarity parameters are the Mach and Reynolds numbers, which represent effects of compressibility and viscosity, respectively. Other forces frequently may enter an aerodynamics problem. By applying the examples given in this chapter, students can address such situations when they arise. The following problem set provides the opportunity for students to test their level of understanding.

Another important feature of the similarity approach is its great utility in planning efficient experiments. Understanding how the many variables interact through the dimensionless similarity parameters enables an experimenter to dras­tically reduce the number of tests needed to determine the significant interactions. It also provides a useful tool for classifying and interpreting various experimental results.

Finally, the stage is now set so that we can explore in more detail, both ana­lytically and numerically, the fascinating problem of flow over aerodynamic bodies and the attendant production of forces that can be used to design efficient flight vehicles.

REFERENCES AND SUGGESTED READING

Anderson, John D., Fundamental Aerodynamics, McGraw-Hill Book Company, New York, 1984.

Kuethe, A. M., and Schetzer, J. D., Foundations of Aerodynamics, 2nd ed., John Wiley & Sons, New York, 1961.

Liepmann, H. W., and Roshko, A., Elements of Gasdynamics, Dover Publications, Inc., New York, 1985.

Prandtl, L., and Tietjens, O. G., Fundamentals of Hydro – and Aeromechanics, Dover Publi­cations, Inc., New York, 1957.

Shevell, Richard S., Fundamentals of Flight, Prentice-Hall, Inc., NJ, 1989.

von Karman, Theodore, Aerodynamics, Selected Topics in the Light of Their Historical Devel­opment, Dover Publications, Inc., New York, 2004.

3.1 Introduction

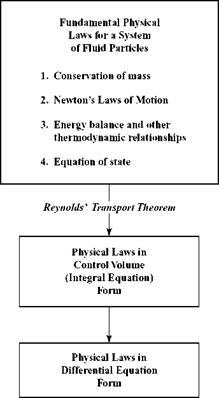
To solve the fundamental problems of aerodynamics defined in Chapter 1, it is necessary to formulate a mathematical representation of the underlying fluid dynamics. The appropriate mathematical expressions or sets of equations may be algebraic, integral, or differential in character but will always represent basic physical laws or principles. In this chapter, the fundamental equations necessary for the solu­tion of aerodynamics problems are derived directly from the basic laws of nature. The resulting mathematical formulations represent a large class of fluid mechanics problems within which aerodynamics is an important subclass.

Some problems in aerodynamics require solutions for all of the variables needed to describe a moving stream of gas—namely, velocity, pressure, tempera­ture, and density. Because velocity is a vector quantity (i. e., with magnitude and direction), in a general case there are three scalar velocity components. Thus, in many cases of interest, there is a total of six unknowns: three velocity components and the scalar thermodynamic quantities of pressure, temperature, and density.[7] This requires six independent equations to be written to solve for the six unknowns. The physical laws of conservation of mass, momentum, and energy supply five such equations (i. e., the momentum equation is a vector equation; therefore, conser­vation of momentum leads in general to three component equations). For all of the subject matter in this book, the assumption of an ideal gas is physically realistic. Thus, the perfect gas law (i. e., equation of state) p = pRT, which relates pressure, density, and temperature, supplies the final equation needed to solve for the six unknowns.

The thermodynamic properties for the various layers can be estimated by solving the appropriate equations. In a gradient layer, such as the troposphere, the tempera­ture is assumed to change linearly in such a way that:

is a constant. Therefore, by integration for a given gradient layer,

T(h) = T + a„(h – hi), (2.30)

where T is the temperature at some altitude h in the gradient layer, n (n = t, s,i, and e stand for troposphere, stratosphere, ionosphere, and so on). Then, from the ideal-gas

equation of state (Eq. 2.1), we can find a relationship among the pressure, altitude, and density:

This then can be inserted into Eq. 2.28 to replace the density so that only the pressure and altitude variables remain. Thus,

where the variables were separated. This simple differential equation can be solved easily by integration, with the result:

where C1 is the constant of integration. Rearranging,

can be evaluated by using known values of p and T at a given altitude. For example, in the troposphere, we can evaluate the constant of integration by using the fact that the sea-level pressure and temperature are pSL = 1.01325 x 105 N/m2 and TSL = 288.16°K. Then, with an = at = -6.5°K/km in the troposphere, and letting the reference point be at sea level (hi = 0, Ti = 288.16°K), the constant of integration is:

Ci = ps{Tsfg/anR).

Now, all the basic properties are available at any altitude in the troposphere gradient layer: Eq. 2.30 gives the temperature, Eq. 2.33 gives the pressure, and Eq. 2.31 gives the density.

Other properties such as the speed of sound and coefficient of viscosity that are mainly functions of temperature also can be determined. For example, the speed of sound, from Eq. 2.6, is:

a = -lyRT,

and using Sutherland’s Law, the viscosity coefficient is 3

2 T0 + S1 T + S :

where for air, S1 = 111°K, and —0 = 1.81 x 10-5 kg/m s and T0 = 273.2°K are reference values. The kinematic viscosity, v, often is needed. It is simply the ratio:

v = kinematic viscosity coefficient = — (2.35)

P

of quantities already known at a given altitude.

Notice that armed with these results, the atmospheric properties can be evalu­ated at any altitude within the layer and at the upper edge of the layer. The latter information then is used to evaluate conditions in the next layer.

Equation 2.28 is the basis of a set of atmospheric representations called standard atmospheres. In fact, there is no accepted standard. Tables of atmospheric prop­erties displayed in many aerodynamics textbooks usually are based on the Air Force ARDC = Air Research and Development Command model atmosphere published in 1959. This model, briefly described herein, is based on radiosonde balloon observ­ations of the temperature distribution in the atmosphere.

Understand that the values predicted by this approximate model represent only an average set of properties. No diurnal or seasonal changes and no geographical effects are reflected in this model. The definition of the model is shown in Fig. 2.8. The temperature distribution through the atmosphere is represented by a set of straight lines. Vertical lines represent “isothermal” layers such as the stratosphere in which temperature changes are negligible. Other layers, such as in the troposphere, are characterized by the rate at which the temperature changes with altitude in an assumed linear manner. The rate of change in a given “gradient” layer is called the lapse rate, denoted by symbols an in the figure. What is significant is that this set of lines defines the temperature, T = T(h), from which all further information can be found by means of the ideal gas equation (Eq. 2.1) and the hydrostatics equation (Eq. 2.28).

Because there is no motion, the ideas of statics yield the information that we need. That is, simple force and moment balances provide all of the necessary relation­ships among variables. In a fluid such as a gas, the forces acting on a fluid element are related to pressure or possibly to surface tension. Viscous forces do not appear because they depend on the presence of a velocity gradient.

Consider the fluid element shown in Fig. 2.7.

This rectangular element has cross-sectional area dA normal to the vertical axis, z. Only the forces in the z-direction are shown because all forces in the lateral direc­tion are mutually balanced. As the figure suggests, the weight of the element, dW, is balanced by the pressure forces acting on the faces of the element. This provides a way to determine how the pressure changes in a body of fluid such as a water tank or the earth’s atmosphere. We use the latter application to illustrate the principles involved.

For static equilbrium in the vertical directions, it is necessary that I F = 0, so that:

pdA – (p + dp)dA – dW = 0. (2.27)

Because the mass of the element is equal to the volume times the density of the material inside, we can write the differential weight as dW = dmg = (pdV)g, where g is the local acceleration due to gravity. If the height of the element is dz, then the volume is dV = dAdz, and the force balance yields dp + pgdz = 0, which can be expressed in differential-equation form as:

This result is often called the hydrostatics equation and it shows how pressure and density are interrelated when there is no motion of the fluid. If the density is known as a function of pressure and the gravitational acceleration is known as a function of z, this equation can be integrated to yield information about the pressure as a func­tion of z. In our application, we interpret z = h to be measured from the earth’s sur­face; it is referred to as the geometric altitude. There are other definitions for altitude that may be useful on occasion. For example, we refer to the pressure altitude as the altitude corresponding to a standard atmospheric value for the static pressure meas­ured outside the vehicle. Equation 2.28 indicates that if the density and gravity were constant, the pressure would decrease linearly with altitude. However, this does not account for observable features of the atmosphere; effects of temperature and den­sity changes also must be considered.