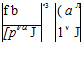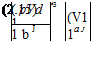Using these ideas, a helpful way to write the expression for the aerodynamic force is:
F = C(M, Re)pV2d2, (2.21)
where the effects of the dimensionless groups now have been incorporated into a coefficient of proportionality, C. For example, what is usually written in aerodynamics problems involving, for example, the lift and drag on an airplane wing is:
|
Lift = L = 1 pV2 SCL
|
(2.22)
|
|
Drag = D = 2 pV2 SCd,
|
(2.23)
|
where the coefficients CL(M, Re) and CD(M, Re) are functions of the appropriate similarity parameters. These are the well-known lift and drag coefficients, respectively. The factor of 1/2 is introduced here to take advantage of the fact that the combination
 dynamic pressure = q =[3] pV[4] [5],
dynamic pressure = q =[3] pV[4] [5],
which has the dimensions of pressure, appears throughout the book as an important aerodynamic parameter. The area, S, is introduced as a convenient substitute for the squared characteristic length, d, which clearly has units of area. Any convenient reference area can be used.
In the study of lift on three-dimensional wings, the reference area, S, usually is chosen as the projected area of the wing surface. Other choices can be made. For instance, in describing the drag of bodies of revolution, we often use the projected frontal area of the body as the reference area, S.
Notice that, by using a combination of physical and dimensional reasoning, we now have reduced the aerodynamic-force problem to a convenient and practical form, which can be applied readily in airplane design, for instance.
Consider the application of Eq. 2.22 for determining, for example, the lift on an airplane wing. Three main elements are involved. One factor, the dynamic pressure, describes the environment—that is, the flight speed and altitude as represented by air density (which, as we shall see, is strongly dependent on altitude). An important geometrical dependence is seen in the reference area, S. Finally, a coefficient, CL, implies a dependence on compressibility and viscous effects because, as demonstrated, its value is a function of the Mach and Reynolds numbers characterizing the flow field. It must be understood that aerodynamic coefficients also are dependent on geometry.
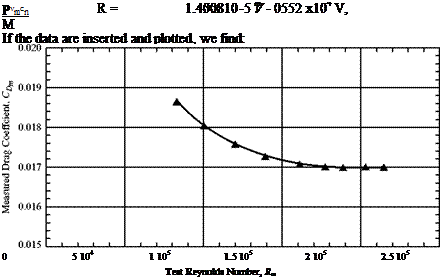
The situation would be simplified if the coefficients were thought of as constants. Then, it would be necessary to compute or measure them only once for a given shape to provide design information for using that shape in a practical application. However, our analysis shows that they vary with special parameters—in this case, the Reynolds and the Mach numbers.
To use Eqs. 2.22-2.23, for example, in a wing-design problem, we must have values for all three factors. The first two are known from the design operating conditions and the geometry. However, how can we determine the lift coefficient? Several approaches naturally come to mind:
Why are there different approaches and how do we determine which is the correct one to use in a given situation? These are important practical questions, and we endeavor to provide the answers in the following discussion. A major objective of this book is to introduce methods for accomplishing Method 1. An introduction to Method 2 also is discussed in considerable detail at approprate points. The numerical approach is rapidly gaining in popularity as large-scale computing costs drop and workstation and desktop computer capabilities improve. Method 3, experimentation, is the traditional approach and still is used extensively for reasons that will become clear. It is also important to observe the relationship between Methods 2 and 3. In many ways, Method 2 is another method of experimentally determining the required information. It represents “virtual” experimentation, which can take the place of a usually more costly physical experiment.
It is of the greatest importance that the student realizes that experimentation, either numerical or physical, cannot be used as a substitute for a thorough theoretical understanding of the problem to be solved. The flow-similarity ideas discussed in this chapter show how important this physical understanding can be. Even lacking an in-depth theory of gas flow over a body, using simple dimensional reasoning, we have identified the correct relationship between the key variables in Eqs. 2.22 and 2.23 for determining aerodynamic forces. Basically, it reduces the problem to one of finding coefficients such as CL and CD.
To illustrate how important such theoretical results can be, consider the following example: Suppose it is your job to design the wing of a new airplane. You consider yourself an experimentalist and do not have much use for theoreticians and their incessant equations. However, you fully understand the thinking that led to Eq. 2.10. You know that there are five key variables. You also understand geometrical similarity, so you proceed to build a scale model of the airplane to be tested in the wind tunnel. Now, if you are not armed with the right theoretical understanding, you probably will think that it is necessary to vary all five of the variables to obtain a full set of data describing how the forces on the wing vary with speed, density, viscosity, size, and so on. If it takes a minimum of five values of each variable over their expected range to determine how they affect the aerodynamic forces, then it is easy to see that it will require 55 = 3,125 separate test runs to acquire the needed information. Keeping in mind the high cost of laboratory space, instrumentation, and technicians, this would turn out to be an expensive and time-consuming exercise; you would most probably lose your job.
Conversely, if you base your experiments on your understanding of the theory, you will see that there are only two parameters to keep track of on a model shaped and oriented like the real prototype: the Reynolds number and the Mach number. The number of experiments needed can be reduced drastically.











 a collection of fluid particles of fixed identity. Visualize a sealed plastic bag filled with liquid or gas that is proceeding downstream in a flow. The contents of the bag constitute a system. Note that if the flow is compressible, the density of the material inside the sealed bag may change. That is, the volume enclosed by the plastic bag may change but the mass of material contained within the bag must remain constant. A system may be finite in size or infinitesimal. An infinitesimal mass of fluid of fixed identity is termed a fluid particle.
a collection of fluid particles of fixed identity. Visualize a sealed plastic bag filled with liquid or gas that is proceeding downstream in a flow. The contents of the bag constitute a system. Note that if the flow is compressible, the density of the material inside the sealed bag may change. That is, the volume enclosed by the plastic bag may change but the mass of material contained within the bag must remain constant. A system may be finite in size or infinitesimal. An infinitesimal mass of fluid of fixed identity is termed a fluid particle.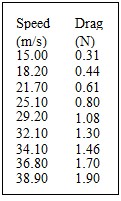 EXAMPLE 2.4 Situation: A 1:10 scale model sailplane wing is tested in a wind tunnel to determine the aerodynamic characteristics. The span of the prototype is 15 m and the average chord (width) of the wing is 0.8 m. Sea-level air is the working fluid for both the model and full-sized wings.
EXAMPLE 2.4 Situation: A 1:10 scale model sailplane wing is tested in a wind tunnel to determine the aerodynamic characteristics. The span of the prototype is 15 m and the average chord (width) of the wing is 0.8 m. Sea-level air is the working fluid for both the model and full-sized wings.