The study of the defining equations begins with the equations in vector form, as derived in Chapter 3. Thus, assuming zero body force and no viscous effects, then:
continuity: V • V = 0 (3.52)
momentum: pdjV + p(V • V)V + VP = 0 (3.66)
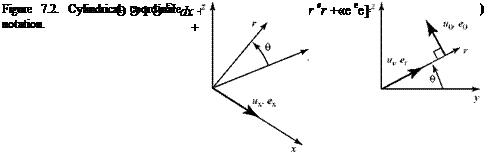
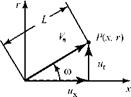
The notation to be used is illustrated in Fig. 7.2. The subscripts on the velocity components emphasize direction—they do not denote partial differentiation of the quantity, as used in some texts. The vector operations in Eqs. 3.52 and 3.66 now are expanded in cylindrical coordinates and then reduced by the assumption of axial symmetry. Because the flow is incompressible, the density, p, is assumed to be constant. We let the local velocity vector be given by:
V = ux ex + U er + ue ee, (7Л)
where ux, ur, and Ue are the velocity components in the cylindrical coordinate directions and ex, er, and ee are the unit vectors in those directions (see Fig. 7.2).
The Continuity Equation
Writing the velocity vector and the divergence operator in cylindrical coordinate notation, Eq. 3.52 becomes:
Notice that the derivatives in the first set of brackets are taken relative to three two – term products in the second set. Thus, applying the chain rule to the d/dx derivative, for example:
(e ж)’ <“■ e ■( ‘■ tf) + ‘■ • (u Жт) (7.3)
A complete expansion of Eq. 7.2 thus contains 18 terms (the student should verify this). These terms fall into the following five different categories:
(1) Three terms contain a vector-dot product of unity, which then multiplies the derivative of a velocity component relative to its own coordinate direction. For example:
3u. du„
p. p ___ x x
Єх Ex Э x Э x.
These three terms are nonzero and are written later.
(2) Six terms contain the derivative of a velocity component relative to another coordinate direction; for example, див/ dr. These six terms are nonzero, but they all appear as the coefficient of a unit vector, which then is dotted into a unit vector at right angles to itself, yielding zero. For example:
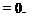 3u0
3u0
dr
Thus, all of these terms drop out in the expansion of Eq. 7.2.
(3)
Three terms contain the derivative of a unit vector relative to its own coordinate direction; namely, 3ex / dx, dee/d0, and deTldr. Because the unit vectors are all of constant length, dej dx and dej dr are zero. The exception is Зе0/ Э0. Derivatives relative to 0 denote changes in direction. Analogous to (5), it may be shown that:
However, this term then is dotted with e0 in Eq. 7.2 so that the contribution of this term is zero as well.
(4) Five terms contain the derivative of a unit vector relative to another coordinate direction. These terms are:
dex der dex de0 d e0
d r ’ dx ’ d0 ’ dx ’ d r
All of these terms are zero because for a differential change in the magnitude of the denominator, there is no change in the magnitude or direction of the numerator unit vector.
(5) One term is an exception to Category (4) namely der / d 0, This term makes a non zero contribution to the equation. To see why, examine Fig. 7.3.
deL = lim (er)2 – (er)r = [(er>1 + B] – (er)
Э0 /vSo A0 A0
У
When introduced into Eq. 7.2 the term containing this derivative then becomes:
Thus, Eq. 7.2 contains four nonzero scalar terms and the continuity equation in cylindrical coordinates becomes:
Continuity Equation—Incompressible Flow—Cylindrical Coordinates
Setting д/д0 = 0 to reduce Eq. (7.6) to axisymmetric flow:
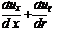
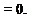
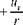 (7.7)
(7.7)
Continuity Equation—Axisymmetric Incompressible Flow
The continuity equation, Eq. 7.7, is sometimes written in a more convenient form (see Eq. 7.18). The student should expand Eq. 7.2, examine each term, and then verify Eq. 7.7.
Now, we contrast the continuity equation in cylindrical coordinates, Eq. 7.7, with the continuity equation in two-dimensional Cartesian coordinates obtained by expanding Eq. 3.52; namely:
dU + dt = 0, (7.8)
о x d z
where u and w are the velocity components in the x and z directions, respectively. The presence of the additional term in the axisymmetric case leads to important differences between two-dimensional planar and axisymmetric problems even though each problem is a function of only two independent variables. This is equally true for a compressible flow.
To verify the presence of this extra term, we rederive the continuity equation for the axisymmetric case by applying the Conservation of Mass principle to a fixed control volume of differential size. The flow is assumed to be steady but compressible for later use. The resulting equation then is simplified so as to describe incompressible flow. (Fig. 7.4).
The mass flux in through faces 1, 2, and 3 is:
(1) pux(rd0dr)
(2) pu0(dxdr)
(3) pur(rd0dx)
and the mass flux out through faces 4, 5, and 6 is:
Terms (2) and (5) are equal in axisymmetric flow because there is no change in flow properties relative to the angle 0 when axial symmetry is assumed (i. e., (p«e) = 0).
d e
Setting the sum of all of these six terms equal to zero by virtue of the conservation of mass for steady flow and then canceling Terms (2) and (5), as well as all like terms of opposite sign, the final result is:
—^(pux)rdxdrd0 – purdrdedx – r-^-(pur) – pdr2d0dx = 0. (7.9)
dr dr dr
The last term in this equation is of higher order than the other terms because it contains a product of differential magnitudes to the fourth power, whereas the three other terms in the equation contain only products of these quantities to the third power. Thus, the last term may be considered negligible (i. e., one order smaller) compared to the other terms in the equation in the limit as dx, dr, and d0 become very small. Recognizing this and then dividing by the common coefficient (i. e., – dxdrde), Eq. 7.9 becomes:
r dx(p ux>+pur+r d0(pur) = ^ (710)
which is valid for steady, compressible, axisymmetric flow. Finally, assuming p = constant, dividing by r, and rearranging:
Notice that Eq. 7.11 obtained by the application of the Conservation of Mass physical concept for an axially symmetric flow, is identical to Eq. 7.7 obtained by
expanding the vector formulation of the general Conservation of Mass equation (Eq. 3.52) for incompressible flow in cylindrical coordinates and then assuming axial symmetry.
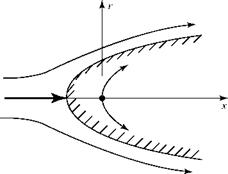 The velocity components ux and ur at any point in the flow field may be evaluated by using Eq. 7.35 in Eq. 7.20.
The velocity components ux and ur at any point in the flow field may be evaluated by using Eq. 7.35 in Eq. 7.20.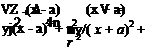
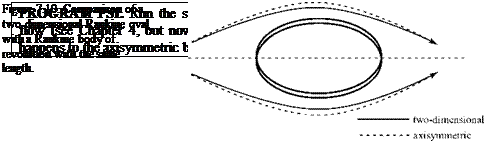











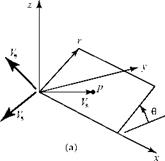

 By definition, the flow is purely radial, with a velocity given by Vs. We consider a fixed spherical control volume surrounding the origin of coordinates, with the center of the sphere at the origin (Fig. 7.6). Then, we make a calculation for the mass flux through the surface of the control volume. Recall that the surface area of a sphere of radius a is given by 4na2.
By definition, the flow is purely radial, with a velocity given by Vs. We consider a fixed spherical control volume surrounding the origin of coordinates, with the center of the sphere at the origin (Fig. 7.6). Then, we make a calculation for the mass flux through the surface of the control volume. Recall that the surface area of a sphere of radius a is given by 4na2.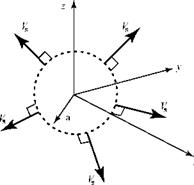 Figure 7.6. Mass flux through fixed control volume.
Figure 7.6. Mass flux through fixed control volume.