Compressible Potential Flows
Since shock waves in practical transonic flows are weak, such flows are nearly isentropic outside the viscous layers, so that their velocity field is nearly irrotational and hence can be represented by the full potential Ф.
V = УФ (8.21)
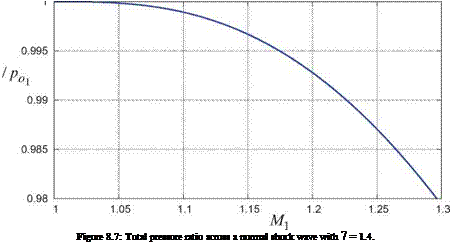
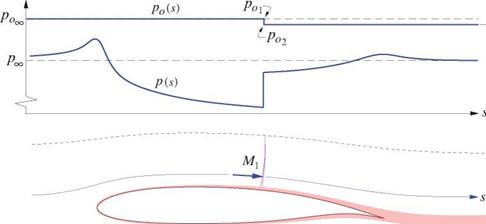
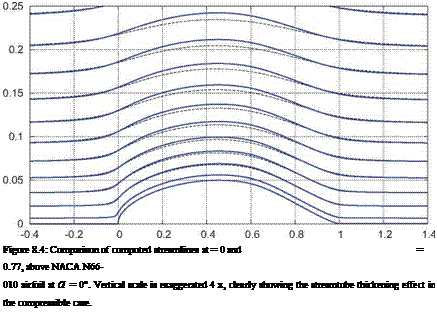
Since this V is irrotational it cannot exactly represent the slightly rotational flow in a shock wake. Specifically, defining V via the full potential will always result in exactly VWake/VL = 1 in the far-downstream shock wake. But as can be seen in Figure 8.9, in typical aerodynamic flows which have weak shock waves this error in the shock’s wake velocity is very small, and the effects on the surface pressures and hence on the lift are small as well. For this reason the slight error in the velocities will be neglected in most of the subsequent compressible potential flow analyses.
An exception is the wave drag, which by definition (8.19) is exactly zero when VWake/VL = 1. This shortcoming will be resolved in Section 8.4.3 where the wave drag is defined in an alternative manner.
8.4.1 Full potential equation – problem formulation
A general compressible potential flow is described by the full potential (FP) equation which governs the full potential field Ф(r; Мж, а,в). The overall FP analysis problem is stated as follows.
(8.22)
Г along the span are additional unknowns, and are constrained with matching Kutta conditions along the span. Only one Г and one Kutta condition is present in 2D.
8.4.2 Full potential solution
Because the isentropic density as given by (8.23) has a complicated nonlinear dependence on УФ, analytic solutions to the FP analysis problem are not possible even for very simple geometries. Instead, solutions must be obtained numerically by using either a finite-volume or finite-element discretization method formulated on a space-filling grid. Such a method is commonly called a Full Potential Solver. If transonic flows are to be computed, some type of modification is also needed in order to capture shock waves. The most common approach is to modify the density in the FP equation (8.22) by an upwinding term proportional to the streamwise gradient of the density. One example of such a modification due to Hafez et al. [57] is
p ^ p – v a£ Vp – УФ/|УФ| (8.27)
where v is the upwinding parameter (comparable to unity in magnitude), and a£ is the local grid cell size. Note that in the limit of a very fine grid we have АІ ^ 0 and the density modification term disappears, so that the equation actually solved is consistent with the analytical FP equation.
Besides the body geometry, the required input parameters to the overall problem are the freestream Mach number ML and the freestream flow angles а, в. The resulting pressure field then has the same functional form as the potential,
so that the integrated force and moment coefficients will then also depend on MTO, а, в (or MTO, a in 2D).











 hwake (A
hwake (A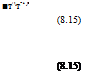

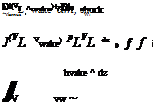
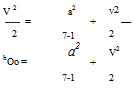
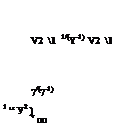

 (8.11)
(8.11)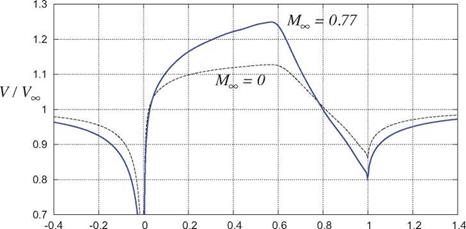

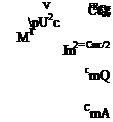
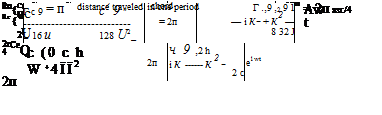
 3
3