ANGULAR VELOCITIES OF THE SEVERAL REFERENCE FRAMES
Since the formulae for velocity and acceleration given above involve the angular velocity of the moving frame, we need convenient expressions for the angular velocities of the frames we shall be using. These expressions are developed below.
ANGULAR VELOCITY и® OF FE AND FEO
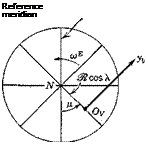
The motion of the Earth consists of a superposition of rotation on its axis, precession and nutation of its axis, rotation in its orbit around the sun, and additional motions of the solar system and the galaxy. Although any of these may be significant for problems of space flight, only the first-mentioned is likely to be of any importance for atmospheric flight, and even that one is often negligible We shall assume therefore that the Earth’s axis is fixed in inertial space, and that its motion is one of constant rotation at speed (oB on this axis. Its angular velocity vector is (see Figs. 4.2 and 5.2)
 (5.2,1)
(5.2,1)
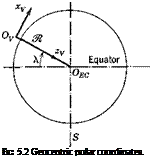
ANGULAR VELOCITY cor OF Fv
Let the origin of Fy be at (A, p) at time t, and let it, in time 8t, undergo infinitesimal displacement to (A + dA, p + dp). It can be carried from its initial to its final positions by the two rotations (i)—6A around an axis
through the Earth center parallel to 0ryr and (ii) 6/t around 0ECzEO. Hence the angular displacement relative to Earth is given approximately by the vector
<5n = —}v 6X + kEC d/i (5.2,2)
where jу and kEO are unit vectors on Ovyv and 0ECzEC, respectively. The angular velocity of Fv relative to FE is then exactly
wv _ мя = lim *5 = _.rx + kEO/i (5.2,3)
st-o 6t
On taking components of (5.2,3) in Fr, and using (5.2,1) we get
(coE + ft) cos X
![]()
 |
 |
v
tli у =
_—{mE + ft) sin A.
The components of (iiV in Fw or FB are, of course, obtained by premultiplying (5.2,4) by Lwv or LBr, respectively.
ANGULAR VELOCITIES taw, w OF Fw, FB
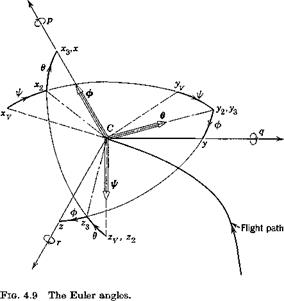
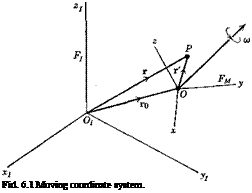
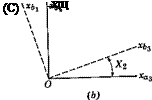
The orientation of the moving frames Fw and FB are given relative to Fr by the Euler angles ip, в, ф (Sec. 4.3). Subscript W denotes Fw and no subscript denotes FB. The result is derived below for FB, that for Fw being similar.
With reference to Fig. 4.9, let i, j, к be unit vectors of FB, the subscripts
Adding the subscript W in (5.2,8) and (5.2,9) to [P, Q, R], ф, 0, y>] gives the corresponding wind-axes equations. Note that these are transcendental differential equations for the Euler angles, and as such have exact analytical solutions only in special simple cases. Note also that the transformation matrix R, unlike L, is not orthogonal.
Equations (5.2,9) can be used to calculate the Euler angle rates from the relative angular velocities (P, Q, R). The latter can in turn be found from the “absolute” rates (p, q, r) by the first equality of (5.2,7), and (5.2,4), i. e.
with a similar equation for wind axes obtained by adding the subscript W and substituting hwv for Ъвг.











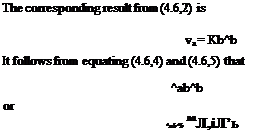
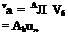 (a)
(a)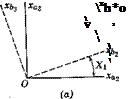
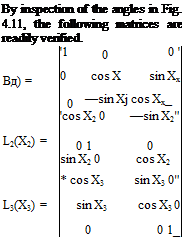 (4.5,2)
(4.5,2)
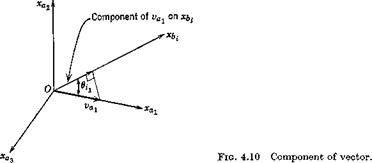
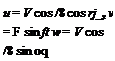 It is most important to note that oq. as here defined will be the same as that commonly used in aerodynamic theory and in wind-tunnel testing only if the body axis Gx is parallel to the basic aerodynamic reference direction, i. e. the mean aerodynamic chord or the zero-lift line. f Otherwise it differs by a constant. When the body axes used are stability axes Fs, the latter will normally be the case. It follows that the velocity components in the body axes are
It is most important to note that oq. as here defined will be the same as that commonly used in aerodynamic theory and in wind-tunnel testing only if the body axis Gx is parallel to the basic aerodynamic reference direction, i. e. the mean aerodynamic chord or the zero-lift line. f Otherwise it differs by a constant. When the body axes used are stability axes Fs, the latter will normally be the case. It follows that the velocity components in the body axes are