2.1 A subsonic transport aircraft has a tapered, untwisted sweptback wing with straight leading and trailing edges. The wing tips are straight and parallel to the root chord. In the following, use the data of Appendix C and assume that the airfoil section local aerodynamic center is at the |-chord point.
(a) Make an accurate three-view drawing of the wing chord plane.
(b) Calculate wing area S, aspect ratio A, taper ratio A = c, lcr and the mean aerodynamic chord c.
(c) Calculate the location of the wing’s mean aerodynamic center, and locate it and c on the side view of the wing (with dimensions). (Assume a uniform additional lift coefficient Cla = CL.)
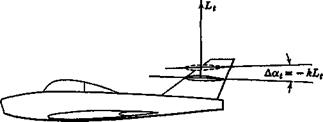
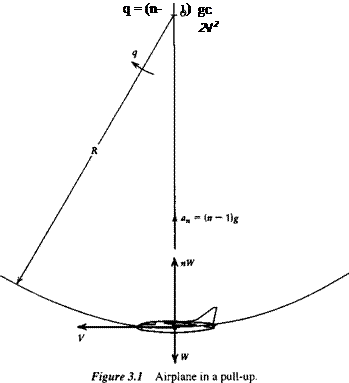
(d) The aircraft is to be operated with its most rearward CG position limited to 25 ft (7.62 m) aft of the apex of the wing. The distance between the wing and tail mean aerodynamic centers is Ї, = 55 ft (16.76 m). Estimate the tail area required to provide a control-fixed static margin of at least 0.05 at all times. Assume that a, = awh and h„w = hnnb. Ignore power plant effects and use дє/да = 0.25.
 Geometric Data Wing Span, b Root Chord, cr Tip Chord, c,
Geometric Data Wing Span, b Root Chord, cr Tip Chord, c,
Leading edge sweep, A0 26°
Dihedral angle, у 4°
2.2 Evaluate the validity of the approximation made in going from (2.2,2) to (2.2,3) by using the data for the airplane of Exercise (2.1) and calculating C,„ r from both equations. Assume CDw = CD + KC ju and L = Lw. The following additional data are provided.
Geometric Data
Weight, W 207,750 lb (924,488 N)
zlc 0.15
Aerodynamic Data
a„ 0.080/deg
Cmacw -0.05
CD 0.013
К 0.054
V 350 kts (180 m/s)
p 2.377 X 103 slugs/ft3 (1.225 kg/m3)
2.3 Show that if Cmwh is a linear function of CLwb then Cm is a constant.
2.4 Beginning with (2.3,1) perform the reductions to derive (2.3,20) to (2.3,23).
2.5 The following data apply to a is scale wind tunnel model of a transport airplane. The full-scale mass of the aircraft is 1,552.80 slugs (22,680 kg). Assume that the aerodynamic data can be applied at full-scale. For level unaccelerated flight at V = 239 knots (123 m/s) of the full-scale aircraft, under the assumption that propulsion effects can be ignored,
(a) Find the limits on tail angle і, and CG position h imposed by the conditions Cmo > 0 and Cma < 0.
(b) For trimmed flight with 8e = 0, plot i, vs. h for the aircraft and indicate where this line meets the boundaries of part (a).
 Geometric Data Wing area, S
Geometric Data Wing area, S
Wing mean aerodynamic chord, c
I
Tail area, S,
Aerodynamic Data
awb 0.077/deg
a, 0.064/deg
e„ 0.72°
Эе
— 0.30
да
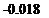 ^™«ч,*
^™«ч,*
Kwh 0.25
p 2.377 X 1(T3 slugs/ft3 (1.225 kg/m3)
2.6* The McDonnell Douglas C-17 is a four-engined jet STOL transport airplane.
(a) Find A and c for the wing using the geometrical data and Appendix C.
(b) Use Appendix В to estimate aw, the wing lift curve slope, assuming that /3 = 1 and к = 1.
(c) If a, = 0.068/deg and awb = aw, find the lift curve slope, a, of the aircraft. As-
дє 2 aw
sume — = —- (with aw expressed in rad da 7tA
(d) Find Cma for the case where l, = 1, = 92 ft (28.04 m). Ignore propulsion effects.
|
* Problem courtesy of Professor E. K. Parks, University of Arizona.
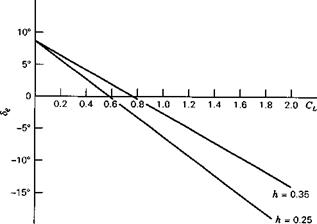
Figure 2.30 Trim data for Exercise 2.6.
|
(e) From the experimental curves of Figs. 2.29 and 2.30 and the given geometry, find Cms and h„. Find Cma for h = 0.30.
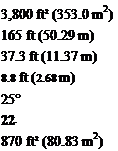 Geometric Data Wing area, S Wing span, b Root chord, cr Tip chord, ct chord line sweep, A chord line sweep, АсП Tail area, St
Geometric Data Wing area, S Wing span, b Root chord, cr Tip chord, ct chord line sweep, A chord line sweep, АсП Tail area, St
2.7 Consider an aircraft with its tail identical to its wing (i. e., the same span, area, chord, etc.). Neglect body and wing-body interaction effects [i. e., in general ( )wh = ( )J, neglect propulsion effects and assume zero elevator and tab deflections. As
sume (2.2,7) in this instance is approximated by M, = ~l, L, + Macr
(a) What changes should be made in the expressions for a (2.3,18), C„a (2.3,21a), and Cm<> (2.3,22a)?
’ де
(b) What would — have to be numerically in order that the neutral point hn lies
da
midway between the mean aerodynamic centers of the wing and tail?
(c) For trimmed level flight, derive an expression for the ratio of the lift generated by the wing to the lift generated by the tail as a function of the tail angle i,. Assume
де,
e„ = 0, — = 0.2, a = 5 (rad’1), Cm = 0.2 and (h – hn) = -0.3. da "
2.8* The following data were taken from a flight test of a PA-32R-300 Cherokee-6 airplane.
|
Altitude (ft) (km)
|
(mph)
|
(m/s)
|
Mass
(slugs)
|
(kg)
|
i,
(deg)
|
XCG
(in)
|
(cm)
|
|
4540
|
1.384
|
91.0
|
40.7
|
113.4
|
1656
|
1.5
|
93.89
|
238.5
|
|
4560
|
1.390
|
109
|
48.7
|
113.0
|
1650
|
0
|
93.89
|
238.5
|
|
4700
|
1.433
|
126
|
56.3
|
112.9
|
1649
|
-1.0
|
93.89
|
238.5
|
|
4580
|
1.396
|
155
|
69.3
|
112.7
|
1646
|
-2.0
|
93.89
|
238.5
|
|
5320
|
1.622
|
89.0
|
39.8
|
100.4
|
1466
|
4.5
|
86.82
|
220.5
|
|
4620
|
1.408
|
105
|
46.9
|
100.2
|
1463
|
2.0
|
86.82
|
220.5
|
|
4740
|
1.445
|
123
|
55.0
|
100.0
|
1461
|
0.3
|
86.82
|
220.5
|
|
4900
|
1.494
|
151
|
67.5
|
99.84
|
1458
|
-1.0
|
86.82
|
220.5
|
|
4880
|
1.487
|
87.0
|
38.9
|
88.51
|
1293
|
7.2
|
80.43
|
204.3
|
|
4820
|
1.469
|
103
|
46.0
|
88.35
|
1290
|
3.5
|
80.43
|
204.3
|
|
4880
|
1.487
|
122
|
54.5
|
88.20
|
1288
|
1.5
|
80.43
|
204.3
|
|
4740
|
1.445
|
152
|
68.0
|
88.04
|
1286
|
0
|
80.43
|
204.3
|
Problem courtesy of Professor E. K. Parks, University of Arizona.
The data were taken in trimmed level flight. xCG is the distance of the CG aft of the nose of the aircraft. The aircraft has an all-moving tail and thus i, is used instead of Se to trim the aircraft. The wing area is S = 174.5 ft2 (16.21 m2).
(a) Plot tail-setting angle, i„ versus the lift coefficient of the aircraft for each of the three CG locations.
(b) Curve fit the data points in (a) with three straight lines having a common intercept (refer to Fig. 2.18).
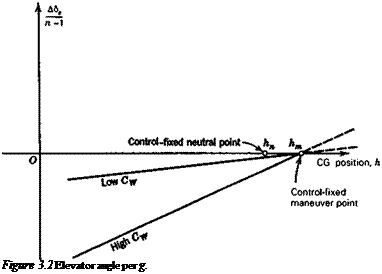
(c) Use a graphical technique to find the location of the neutral point (controls fixed) relative to the nose of the aircraft (refer to Fig. 2.21).
2.9 Starting with (2.6,11 b), derive (2.6,13).
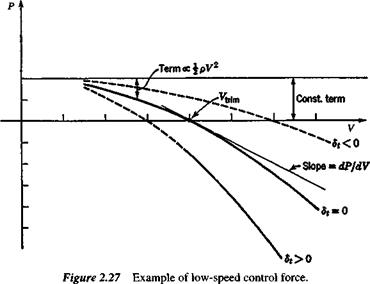
2.10 The elevator control force to trim a particular airplane at a speed of 300 kts (154 m/s) is zero. Using the following data estimate the force required to change the trim speed to 310 kts (159 m/s). Assume that is sufficiently small that = 0 can be used in the expression for control force.
Geometric Data
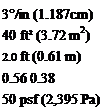 Elevator gearing, G Elevator area aft of hinge line, Se Mean elevator chord, ce VH
Elevator gearing, G Elevator area aft of hinge line, Se Mean elevator chord, ce VH
CG location, h Wing loading, w
Aerodynamic Data
Elevator hinge moment coefficient,
Э Ch
-jf – —0.005/deg
ae 0.025/deg
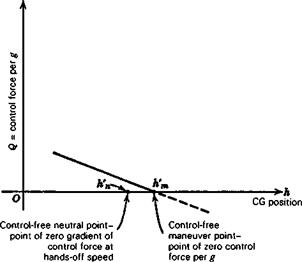
Neutral point, elevator free, h’n 0.45
![]()












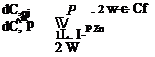
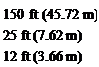 Geometric Data Wing Span, b Root Chord, cr Tip Chord, c,
Geometric Data Wing Span, b Root Chord, cr Tip Chord, c,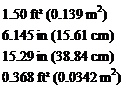 Geometric Data Wing area, S
Geometric Data Wing area, S

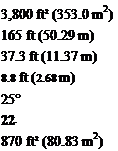 Geometric Data Wing area, S Wing span, b Root chord, cr Tip chord, ct chord line sweep, A chord line sweep, АсП Tail area, St
Geometric Data Wing area, S Wing span, b Root chord, cr Tip chord, ct chord line sweep, A chord line sweep, АсП Tail area, St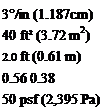 Elevator gearing, G Elevator area aft of hinge line, Se Mean elevator chord, ce VH
Elevator gearing, G Elevator area aft of hinge line, Se Mean elevator chord, ce VH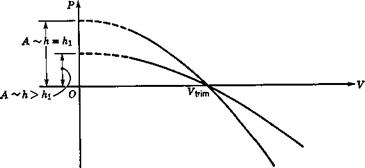
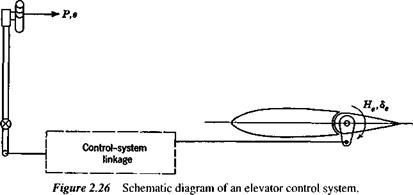
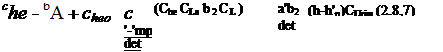
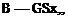 M, + Cheo + (CheCLSe – b2CLa)
M, + Cheo + (CheCLSe – b2CLa)