MEAN SQUARED ERROR
The mean squared error (MSE) of an estimator of a parameter is the expected value of the square of the difference between the estimator and the parameter. It is given as MSE(p) = E{(P — P)2}. It measures how far the estimator is off from the true value on the average in repeated experiments.
B17 MEDIAN AND MODE
The median is a middle value: the smallest number such that at least half the numbers are no greater than it. If the values have an odd number of entries, the median is the middle entry after sorting the values in an increasing order. If the values have an even number of entries, the median is the smaller of the two middle numbers after sorting. The mode is a most common or frequent value. There could be more than one mode. It is a relative maximum. In estimation, data affected by random noise are used, and the estimate of the parameter vector is some measure or quantity related to the probability distribution; it could be mode, median, or mean of the distribution. The mode defines the value of x for which the probability of observing the random variable is a maximum. Thus, the mode signifies the argument that gives the maximum of the probability distribution.











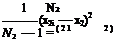 1 N
1 N