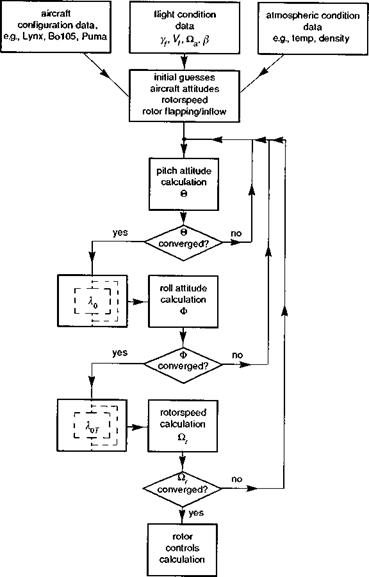
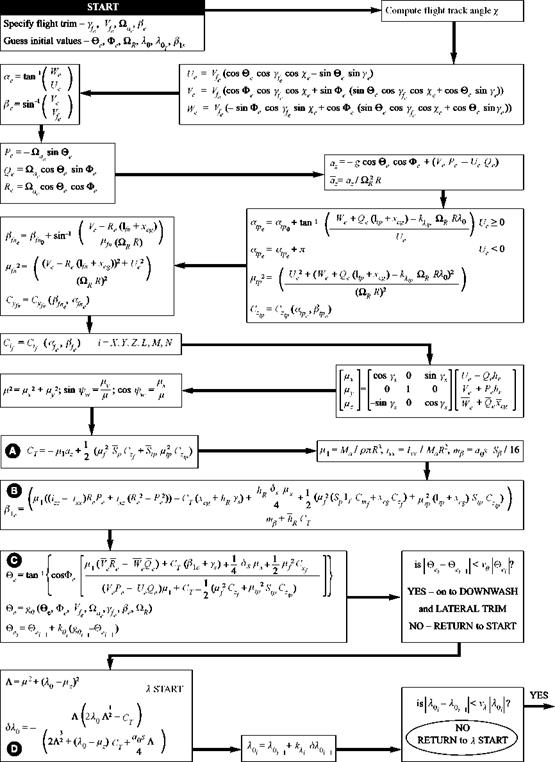
At this point in the trim algorithm, the various forces and moments on the components are, practically speaking, balanced, and now we have to look at the internal rotor equations to compute the controls required to hold these forces. The main rotor control angles are derived from the inverse of the flapping angle calculations given in the 3.60 series of equations (see Chapter 3), coupled with the thrust coefficient equation for the collective pitch. Figures 4.10(a)-(d) show a comparison between flight and theory of the main and tail rotor controls for the Bo105 as a function of forward speed. The errors give an indication of the level of fidelity achievable with the Level 1 modelling of Chapter 3. The nonlinear aerodynamic and blade twist effects increase the collective pitch required in flight relative to Helisim. As noted above in the discussion on longitudinal trim, the downwash over the tail causes a pitch up in the low-speed regime, giving rise to an increase in the required forward cyclic; the comparison for the Bo105 is actually very good in the mid-speed region (Fig. 4.10(a)). Also at low speed and into the transition region, the inflow roll increases the left cyclic required, revealing a failing in the simple trapezoidal model of longitudinal inflow predicted by the Glauert representation (Fig. 4.10(b)). The comparison of main rotor collective pitch is illustrated in Fig. 4.10(c). The underprediction by about 10% in hover, increasing to over 30% at high speed, is typical of linear aerodynamic theory. The tail rotor pitch is also usually underpredicted (Fig. 4.10(d)) as a combined result of missing tail rotor losses
|

Fig. 4.10 Bo105 control angles in level trimmed flight: (a) longitudinal cyclic; (b) lateral cyclic; (c) main rotor collective; (d) tail rotor collective
|
and underpredicted main rotor torque, most noticeably at high speed. At moderate – to high-speed flight, the absence of tail rotor flapping and the powerful interactions with the aerodynamics of the rear fuselage and vertical fin increase the modelling discrepancies.
The power required, shown in Fig. 4.11 for the Bo105, has the characteristic bucket profile as a function of forward speed, reflecting the reduction in induced (rotor drag) power and increase in parasite (fuselage drag) power as speed increases. At high
|
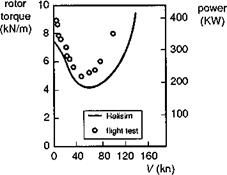
Fig. 4.11 Bo105 power required as a function of forward speed
|
speed, nonlinear rotor aerodynamic terms have a significant effect on collective pitch and power required, leading to the gross errors with the simplified Level 1 modelling as shown by the comparison withBo105 flight test data in Figs 4.10(c) and4.11. For moderate rates of climb and descent, the Level 1 theory predicts the basic trends in power required and control angles fairly well. The rotor is particularly efficient in climbing flight. While the power required to climb a fixed-wing aircraft is approximately equal to the rate of change of potential energy, the increased mass flow through the rotor of a helicopter reduces the power required to half this value. For similar reasons, the rotor is inefficient in descent, the power reduction corresponding to only half the rate of loss of potential energy. These simple results are explicable through the momentum theory of Level 1 modelling. In steep descent, however, strongly nonlinear aerodynamic effects dominate the trim (and stability and response) requirements. We have already discussed the vortex-ring region in both Chapters 2 and 3 and highlighted the inadequacy of simple momentum theory for predicting the power required and response characteristics. On the other hand, for higher rates of descent, between vortex ring and autorotation, the empirical modifications to momentum theory discussed in Chapter 3 provide a reasonable interpolation between the helicopter and windmill solutions to the momentum equations for rotor inflow. An analysis of trim requirements in helicopter descending flight is reported by Heyson in Ref. 4.3. At steep angles of descent, and flight speeds of about 1.5 times the hover induced velocity, the power required to increase the rate of descent actually increases. Figure 4.12, taken from Ref. 4.3, illustrates the power required as a function of glide slope angle for several different values of flight speed along the glide slope. The reference velocity wh and power Ph correspond to the hover values, otherwise the results are quite general. At steep angles of descent (>60°), the power required to increase the rate of descent at a constant speed increases. Also shown, in Fig. 4.12(b), is a power contour for the rotor pitched up by
|
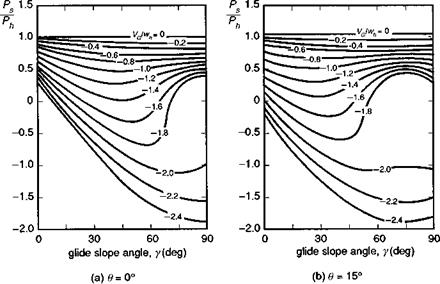
Fig. 4.12 Power required in descending flight (from Ref. 4.3): (a) в = 0°; (b) в = 15‘
|
15°, showing the expanded region of increased power required as a function of flight path angle. Heyson refers to this, and the associated response characteristics, as power settling, and comments on the operational significance of this strong nonlinearity. To quote from Heyson’s report,
A pilot flying a steep approach generally flies with reference to the ground either visually or through the use of some avionic system. Although he can sense sidewinds as a drift, his perception of a headwind or tailwind is poor. Even a light tail wind can produce a major difference between the glideslope with respect to the surrounding air mass and the geometric glideslope. If the flight is stabilised near one of the minimum power points, Fig. 12 shows many combinations of у, в, and VG/wh for which a tailwind induced change of only 10° or 15° in у increases the required shaft power by 50 to 100% of the installed power. In the presence of such a major increase in required power, the helicopter settles, thus increasing the glide slope and still further increasing the required power.
With the above discussion on steep descent, we have strayed into the response domain, showing the importance of predictable trim characteristics to the pilot’s flying task. We shall return to this aspect in Chapters 5 and 7.
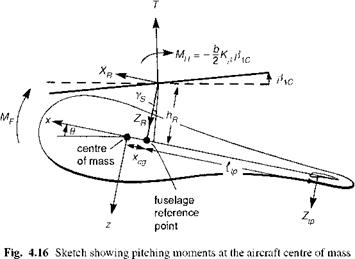
Predicting the trim control angles required, the power required and the steady loads on the various components forms a basis for calculating such static characteristics as the control margins at the flight envelope boundary, payload and range capabilities and limit loads on the tail boom in sideslipping flight. Achievement of accurate estimates (e. g., to within a few per cent of the true values) of such parameters will almost certainly require more detailed modelling than that described in the above analysis. The main rotor forces are a more complex function of rotor motion and the aerodynamics can be strongly nonlinear in high speed or at high thrust coefficient. The fuselage and empennage forces can be strongly influenced by the rotor wake and the tail rotor flapping can tilt the disc and thrust vector and change the power required. In some cases these will be first-order effects and cannot be ignored. Certainly, the component interactions will tend to spoil the simple sequential nature of the algorithm described above, giving rise to many more potential convergence problems and demanding more sophistication in the iterative solution. For trend predictions, however, the simple theory can be remarkably accurate; the characteristic shapes of the trim control curves is evidence of this. Examination of the effects of small changes from some baseline configuration can also provide useful insight into the sensitivities to design configuration or flight state parameters.
Trim solutions are generally unique, with a fixed set of control positions defining each equilibrium condition. A natural question that arises out of the study of trim is what happens if the aircraft is disturbed by a small amount from the trim? This could happen with a small gust or nudge of the controls. Will the aircraft immediately settle into a new trim, return to the original trim or depart away from the trim state in an unstable fashion? These questions cannot be answered from analysis of the trim equations; they require the full dynamic equations of motion from which the time evolution of the flight trajectory and fuselage attitudes can be determined. While a wide flight envelope simulator will usually require the full nonlinear equations, the answers to our questions regarding the effects of small perturbations can generally be found through analysis of the linearized equations using the concepts of the stability and control derivatives.
The concept of stability of motion in a dynamic system is a very intuitive one that grasped the imagination of early pioneers of aviation. The supporting archetypal theory for flight stability was developed in the very early days of manned flight (Refs 4.2 and 4.4). The concept that stability and control were unlikely partners, the latter gaining from shortcomings in the former, was also recognized in these same early days, such that marginal stability, or even instability, was actually a useful property when considering the required piloting effort. Since that time much has been written on stability and control and much of the theoretical foundation for the stability of low-speed fixed- wing aircraft was already well developed by the time that early helicopters were in serious development. The first helicopters were unstable but the presence of mild instabilities at low speed was probably something of a blessing because control power was fairly marginal on these early craft. While fixed-wing aircraft have developed and can easily be conferred with high levels of natural stability and compatible levels of control, basically helicopters are still naturally unstable and require some level of artificial stabilization to ensure safe control in poor weather and when flying under instrument flight rules (IFR). The degree of stability required in helicopters to ensure safe operations is an important flying quality consideration, and will be discussed in some detail later in Chapter 6.
Understanding the flight behaviour of helicopters, why they are so difficult to build with natural stability, and developing rational explanations for the many curious dynamic characteristics, cannot be achieved simply through deriving the equations of Chapter 3, or even by building a simulation model. These are necessary but insufficient activities. The development of a deep understanding of flight behaviour comes from the intellectual interplay between theory and practice, with an emphasis on handson practice and analytical theory. Most of the understanding of stability and control has come from relatively simple theoretical approximations that permit expression of cause and effect in parametric form. Coincidentally, the publication of the earliest texts that provided a definitive treatment of both fixed – and rotary-wing stability and control occurred in 1952 (Refs 4.2, 4.5). Both of these texts deal with fundamental concepts in analytical terms that are still valid today. While our ability to model more and more complex representations of the aerodynamics and dynamics of aircraft seems to extend every year, our understanding of why things happen the way they do essentially comes from simple theory melded with a good physical understanding.
With these words of introduction we embark on this section on stability (and control) with the guiding light in search of simple approximations to complex behaviour. We shall draw heavily on the theory of linear dynamic systems but the underlying vector-matrix theoretical methods, including a discussion on eigenanalysis, are contained in Appendix 4A, to which the unfamiliar reader is referred. Features of the classical description of aircraft stability are the concepts of static and dynamic stability, the former relating to the immediate behaviour following a disturbance, the latter to the longer term behaviour. These are useful but elementary concepts, particularly for fixed-wing aircraft, drawing parallels with stiffness and damping in a simple mechanical analogue, but the distinction is blurred in the study of helicopter motion because of the stronger couplings between longitudinal and lateral motions. The perspective we shall take here is to draw the distinction between local and global stability – the former relating to the stability of motion following small disturbances from a trim condition, the latter relating to larger, potentially unbounded motion. Of course, unbounded motion is only a theoretical concept, and ultimately the issue is likely to be one of strength rather than stability in this case. Analysis tools for large nonlinear motions of aircraft are limited and tend either to be based on the assumption that the motion is nearly linear (i. e., nonlinearities are weak), so that approximating describing functions can be used, or to be applicable to very special forms of strong nonlinearity that can be described analytically.
Nonlinear analysis of fixed-wing aircraft has been stimulated by such phenomena as stall (including deep stall), spinning, inertial coupling and wing rocking. The need to understand the flight dynamics in these situations has led to extensive research into analytical methods that are able to predict the various kinds of departure, particularly during the 1970s and 1980s (Ref. 4.6). Helicopter flight dynamics also has its share of essentially nonlinear phenomena including vortex-ring state, main rotor wake-tail rotor interactions, rotor stall and rotor wake-empennage interactions. Much less constructive analytic work has been done on these nonlinear problems, and many potentially fruitful areas of research need attention. The methods developed for fixed-wing analysis will be equally applicable to helicopters and, just as the transfer of basic linear analysis techniques gave the helicopter engineers considerable leverage in early days, so too will the describing function and bifurcation techniques that have enabled so much insight into the dynamics of fixed-wing combat aircraft. Nonlinear problems are considerably more difficult than linear ones, one consolation being that they are usually considerably more interesting too, but little has been published to date on nonlinear helicopter flight dynamics.
In this chapter we restrict the discussion to linear analysis. We shall consider classical 6 DoF motion in detail. This level of approximation is generally good for low-moderate frequency, handling qualities analysis. The assumption underlying the 6 DoF theory is that the higher order rotor and inflow dynamics are much faster than the fuselage motions and have time to reach their steady state well within the typical time constants of the whole aircraft response modes. This topic has been discussed in the Tour of Chapter 2 and the conditions for validity are outlined in Appendix 4A.
4.3.1 Linearization
Consider the helicopter equations of motion described in nonlinear form, given by
x = F(x, u, t) (4.35)
In 6 DoF form, the motion states and controls are
x = {u, w, q, 9, v, p, ф, r, ф}
where u, v and w are the translational velocities along the three orthogonal directions of the fuselage fixed axes system described in Appendix 3A; p, q and r are the angular velocities about the x-, y- and z-axes and 9, ф and ф are the Euler angles, defining the orientation of the body axes relative to the earth.
The control vector has four components: main rotor collective, longitudinal cyclic, lateral cyclic and tail rotor collective
u = 91s, 91c, 90T }
The expanded form of eqn 4.35 can be written as eqn 4.36 combined with the Euler angles, eqn 4.37 (inverse of eqn 3A.42), as derived in Chapter 3 and Appendix 3A.
X
U = —(wq — vr) +——————– g sin в
Ma
Y
V = —(ur — wp) +——————- + g cos в sin ф
Ma
Z
w = —(vp — uq) +——————- + g cos в cos ф
Ma
hxp = (Iyy — Izz)qr + Ixz(r + pq) + l
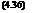
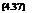 lyyq = (Izz — Ixx)rp + Ixz(r — p ) + M
lyyq = (Izz — Ixx)rp + Ixz(r — p ) + M
Izzr = (Ixx — Iyy) pq + Ixz( p — qr) + N
ф = p + q sin ф tan в + r cos ф tan в
в = q cos ф — r sin ф
ф = q sin ф sec в + r cos ф sec в
Using small perturbation theory, we assume that during disturbed motion, the helicopter behaviour can be described as a perturbation from the trim, written in the form
x = xe + Sx (4.38)
A fundamental assumption of linearization is that the external forces X, Y and Z and moments L, M and N can be represented as analytic functions of the disturbed motion variables and their derivatives. Taylor’s theorem for analytic functions then implies that if the force and moment functions (i. e., the aerodynamic loadings) and all its derivatives are known at any one point (the trim condition), then the behaviour of that function anywhere in its analytic range can be estimated from an expansion of the function in a series about the known point. The requirement that the aerodynamic and dynamic loads be analytic functions of the motion and control variables is generally valid, but features such as hysteresis and sharp discontinuities are examples of non-analytic behaviour where the process will break down. Linearization amounts to neglecting all except the linear terms in the expansion. The validity of linearization depends on the behaviour of the forces at small amplitude, i. e., as the motion and control disturbances become very small, the dominant effect should be a linear one. The forces can then be written in the approximate form
X = Xe + —— Su + —— Sw + ••• + —— 5во + ■■■, etc. (4.39)
d u d w дво
All six forces and moments can be expanded in this manner. The linear approximation also contains terms in the rates of change of motion and control variables with time, but we shall neglect these initially. The partial nature of the derivatives indicates that they are obtained with all the other DoFs held fixed – this is simply another manifestation of the linearity assumption. For further analysis we shall drop the perturbation notation,
hence referring to the perturbed variables by their regular characters u, v, w, etc., and write the derivatives in the form, e. g.,
д X д L
dU = Xu ’ зеГс = Lв1с ’ etc’ (4.40)
The linearized equations of motion for the full 6 DoFs, describing perturbed motion about a general trim condition, can then be written as
x – Ax = Bu(t) + f(t) (4.41)
where the additional function f(t) has been included to represent atmospheric and other disturbances. Following from eqn 4.40, the so-called system and control matrices are derived from the partial derivatives of the nonlinear function F, i. e.,
and
In fully expanded form, the system and control matrices can be written as shown in eqns 4.44 and 4.45 on page 212. In eqn 4.44 the heading angle ^ has been omitted, the direction of flight in the horizontal plane having no effect on the aerodynamic or dynamic forces and moments. The derivatives are written in semi-normalized form, i. e.,
where Ma is the aircraft mass, and
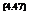 I’ – Izz 1 Ixz N
I’ – Izz 1 Ixz N
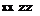 Lp = I I _ 12 Lp + I I _ 12 Np
Lp = I I _ 12 Lp + I I _ 12 Np
ixxizz ly"r lxx*77
Ixx and I77 are the roll and yaw moments of inertia and Ixz is the roll/yaw product of inertia. The к constants in the inertia terms in eqn 4.44 are given by the expressions

|
Ixz( Izz + Ixx Iyy)
Ixx I77 — IXz
|
|
|
|
|
|
Izz (Izz Iyy) + Ixc:
Ixx I77 — Iiz
|
|
|
|
|
|
Ixx (Iyy – Ixx) – Ilz
Ixx Izz — Ixz
|
|
|
|
|
In addition to the linearized aerodynamic forces and moment, eqn 4.44 also contains perturbational inertial, gravitational and kinematic effects linearized about the trim condition defined by
Фе, &e, Ue, , We, Pe, Qe, Re
The trim angular velocities are given in terms of the aircraft turn rate in eqns 4.29-4.31.
Equation 4.41 is the fundamental linearized form for describing the stability and response of small motion about a trim condition. The coefficients in the A and B matrices represent the slope of the forces and moments at the trim point reflecting the strict definition of the stability and control derivatives. Analytic differentiation of the force and moment expressions is required to deliver the exact values of the derivatives. In practice, two other methods for derivative calculation are more commonly used, leading to equivalent linearizations for finite amplitude motion. The first method is simply the numerical differencing equivalent to analytic differentiation. The forces and moments are perturbed by each of the states in turn, either one-sided or two-sided, as illustrated conceptually in Fig. 4.13; the effect of increasing the perturbation size is illustrated in the hypothetical case shown in Fig. 4.13(b), where the strong nonlinearity gives rise to a significant difference with the small perturbation case in Fig. 4.13(a). The numerical derivatives will converge to the analytic, true, values as the perturbation size reduces to zero. If there is any significant nonlinearity at small amplitude, then the slope at the trim may not give the best ‘fit’ to the force over the amplitude range of interest. Often, larger perturbation values are used to ensure the best overall linearization over the range of motion amplitude of interest in a particular application, e. g., order 1 m/s for velocities and 0.1 rad for controls, attitudes and rates. In each case it is important to estimate the degree of nonlinearity over the range of interest, as the derivative value used can have a significant effect on stability and response characteristics.
Before we examine the derivatives themselves in more detail we should refer to the second ‘numerical’ method for deriving derivative estimates. This involves a fitting or model-matching process whereby a linear model structure is used to fit the response of the nonlinear simulation model. This method can also be applied to flight data and is described under the general heading – system identification. We discussed the approach briefly in Chapter 2 and we shall give more attention to applications in Chapter 5. The system identification approach seeks to find the best overall model fit and, as such, will embody the effects of any nonlinearities and couplings into the equivalent
|
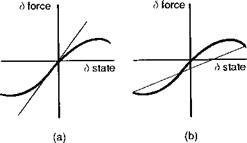
Fig. 4.13 Derivative calculation by backward-forward differencing: (a) small perturbation;
(b) large perturbation
|
derivative estimates. The states are no longer perturbed independently; instead, the nonlinear model, or test aircraft, is excited by the controls so that the aircraft responds in some ‘optimal’ manner that leads to the maximum identifiability of the derivatives. The derivatives are varied as a group until the best fit is obtained. How these estimates relate to the pure analytic and numerical equivalents will depend on a number of factors, including the degree of nonlinearity, the correlation between states in the response and the extent of the measurement noise on the test data. In this chapter we shall discuss only the analytic and numeric methods of derivative estimation, returning briefly to the global system identification approach in the applications in Chapter 5.
![]() двіс 26
двіс 26![]() 16
16![]()
![]() ^ = Ct (1.5________________ ^ = Ct (1.5_________________________ 0L-
^ = Ct (1.5________________ ^ = Ct (1.5_________________________ 0L-