It is possible to estimate the theoretical minimum touchdown speed resulting from an idealized engine-off landing using some of the concepts introduced above [2.6 and 2.27]. The flare angle that can be employed will be affected by the maximum pitch rate that can be generated and the time the pilot has to level the aircraft. During the level manoeuvre, because the helicopter is still moving forward, it can be assumed that OGE hover power and thrust must be maintained even though the rotor speed is rapidly decaying. Since useable energy is stored in the rotor in the form of kinetic energy of rotation if the pilot could allow the rotor speed to decay to zero at touchdown then he could make use of the theoretical maximum, given by:
maximum energy available = 2 I)2om
Unfortunately this is not possible since as the rotor speed decays the angle of attack must be increased if the thrust produced is to remain constant. Consequently the thrust coefficient, or rotor blade lift coefficient, will rise, as NR reduces, up to some maximum value beyond which rotor performance is not sustainable. Hence:

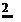 useable energy = 21()
useable energy = 21()
Since:
) =) “min ЙЬпош
then:
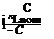 useable energy = 21)
useable energy = 21)
This energy is used to provide hover power and therefore the available time during which the pilot must level the helicopter will be given by:
|
time available to level aircraft = *t =
|

Thus:
Y )
0max = aTPPmax = qmax*t = 16 *Bl*t
Therefore 0max is the maximum fuselage pitch angle change that can be generated in the time available. If this calculated angle exceeds 45° then, as suggested above, 45° is used since this angle gives the theoretical maximum reduction in both horizontal and vertical velocities. (In many instances the pilot will be very reluctant to flare by more than 25% being concerned about either a tail strike or loss of forward vision.)
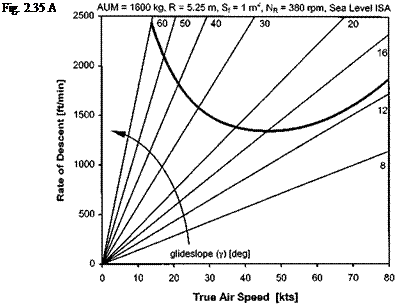
Having determined the flare angle, the forward speed achieved before the pilot begins to level the aircraft is then related to an equivalent stable autorotative condition. This simple approximation assumes that the flare reduces the sink rate to approximately zero. From Fig. 2.34, which shows the glide geometry, it can be seen that just before the helicopter is rotated nose-down the forward advance will equal the value of Vg, or Vf cos 0max, obtained from steady autorotative data.
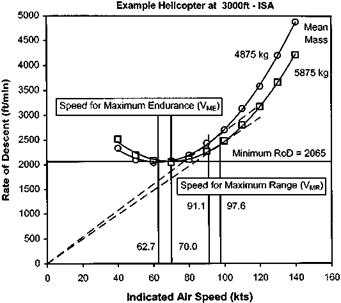
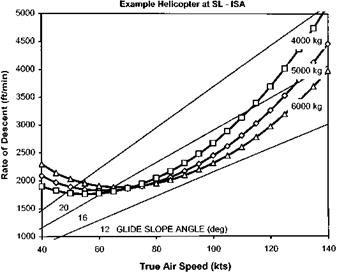
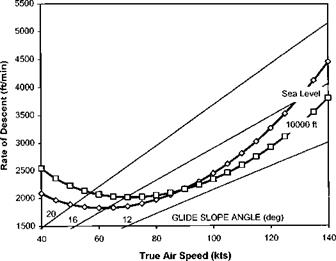
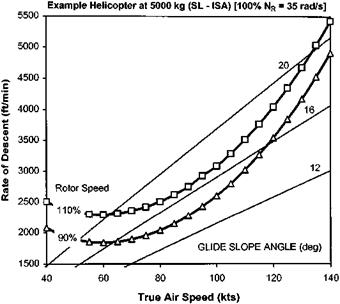
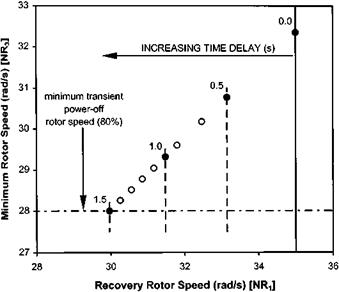
Figure 2.35 shows the steady autorotative performance for an example helicopter. At an AUM of 1600 kg this helicopter will be operating at a mean lift coefficient of 0.133, given by:
2mg
P )2ош bcR1
Under sea level, ISA conditions the rotor speed at 75% rotor radius equates to 0.45M and the hover power is 196.6 kW. If the rotor has an inertia of 1000 kgm2 and is fitted with a NACA 0012 aerofoil then CLmax is approximately 1.0 and At equals 3.5 s. Such a large value of At gives the pilot plenty of time to level the aircraft. Therefore the only concern for the pilot when selecting a flare angle is ensuring that a reasonably low run-on speed is achieved without undue risk to the tail boom and empennage.
Just before the pilot begins to level the aircraft vertical forces are assumed to be in equilibrium. As the aircraft is levelled a steadily diminishing rearwards component of thrust continues to provide a decelerative force. The average deceleration is therefore give by:
F T
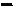
a = — = — sin 0 m 2m
But:
Therefore, assuming a constant deceleration, the velocity reduction during the level manoeuvre is determined using:
|
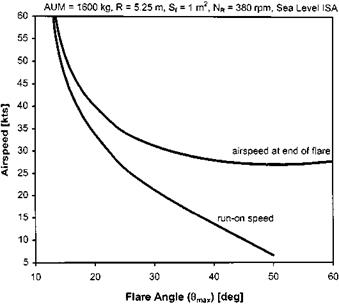
Fig. 2.36 Effect of flare angle on run-on speed.
|
g
A v = aAt = 2 tan 0max At
This relationship indicates that if the pilot is able to select a high flare angle he can significantly reduce the run on speed. Figure 2.36 shows the reduction in speed that can be achieved at various flare angles.
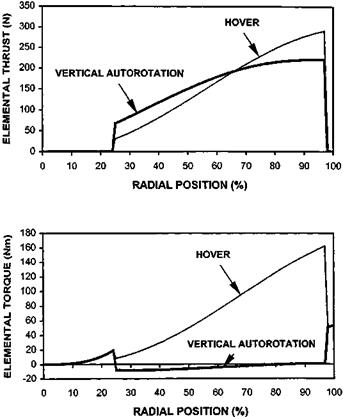
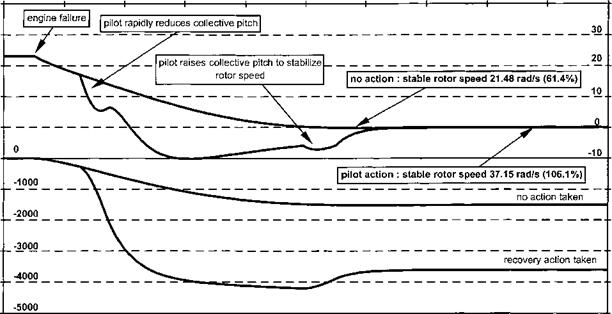
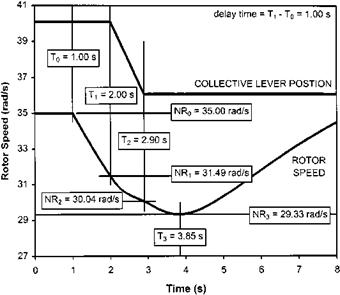
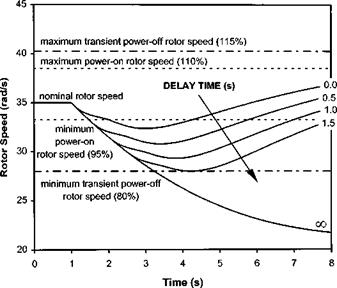
In practice the method described here gives reasonable approximations to the minimum possible run-on speed although it ignores important actions the pilot will typically make in a real EOL. First it is common practice to allow NR to increase during the flare, this capitalizes on the natural tendency of the rotor to accelerate and, at the expense of a slightly higher closure rate, puts energy into the rotor for use during the ‘check’. During the check, a manoeuvre not included in the previous analysis, the collective pitch is rapidly increased causing a temporary rise in thrust and further reducing the glide velocity below that determined by the pitch attitude. Note also that some helicopters will accelerate if levelled completely.
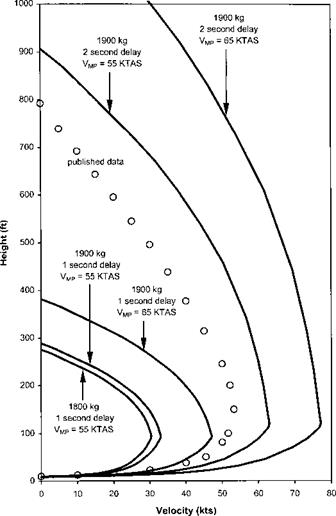
Even in the most advantageous circumstances with tight control of airspeed and rotor RPM maintained during a period of stable autorotative flight, the pilot must still assess the optimum time to commence the flare manoeuvre with a high degree of accuracy. If the flare is commenced too high or too low the subsequent landing may be more hazardous than necessary! Equally if the airspeed on entry to the flare is excessive the flare will be less effective in reducing the horizontal velocity component resulting in a high run-on speed. Alternatively if the airspeed on initiation of the flare is too low insufficient rotor energy may be available to cushion the landing. Consequently within the qualification process for new single-engined helicopters there will be an EOL testing phase during which flares at various combinations of airspeed and
height will be performed. Such tests will be conducted in order to determine which combination minimizes the difficulty of the complete engine-off landing.











 20
20