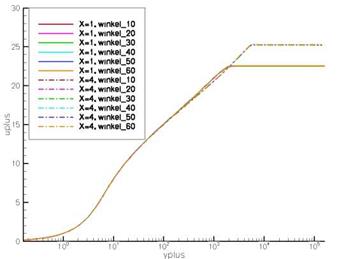
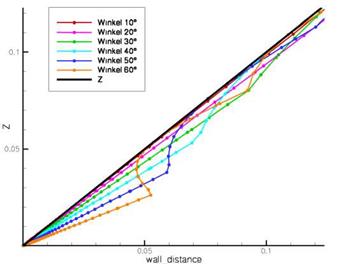
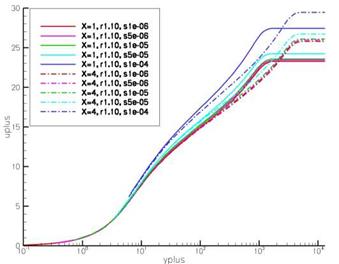
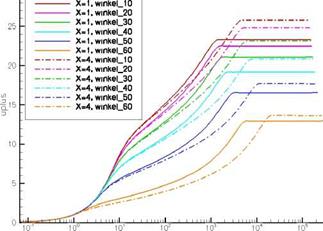
Implementation of the Separation Sensor
As already mentioned the development of the boundary layer with different turbulence models leads to different gradients in the friction coefficients. This implies, depending on the position and choice of model, a premature or delayed separation. A constant dependence between model and separation is not identifiable. The user only gets a feedback about an existing separation effect and the critical areas are marked as a surface value in the output files. To detect the appearance of separation
|
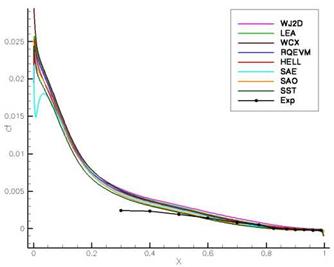
Fig. 12 ONERA-A — friction coefficient Cf in comparision with the eight different turbulence models and the experiment |
the sensor scans the surface for characteristic points (first order) of separation or reattachment. For this every surface triangle is tested. Every triangle element which contains two zero-crossings along the edges in the wall-tangential velocities includes a critical point. In the code the velocity at the wall is represented by the components of Cf. These marked elements include hyperbolic points (the beginning or end of a separation line) or rotation points (a vortex separation). To exclude stagnation areas a minimal pressure coefficient of cp < 0.5 is assumed.