Category Management and Minimisation of Uncertainties and Errors in Numerical Aerodynamics

Within the stochastic analysis, the impact of random input parameters on the static aeroelastic response of the transport aircraft wing is investigated. Based on the res­ults of the sensitivity analysis the analysis is performed at first only for skin areas due to the crucial impact on the wing aerodynamics. The wing structure is divided into four areas in which the input parameters were independently varied. The divi­sion of the areas is given in table 6 as a function of the span co-ordinate.

In each area, the structural parameters were varied simultaneously in the top and bottom skin parts. By this simplification, the number of random variables Xi decreased to a total of four that in turn led to significant reduction of numerical expenditure.

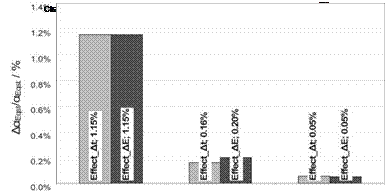
The Gaussian normal distribution for random input parameters is assumed (see section 3.2). To estimate the coefficient of variance for the thickness distribution manufacturing data sheets for maximum thickness deviation were analyzed. Fol­lowing this analysis, a coefficient of variance, which lies between 0.02 and 0.04, seems to be realistic, but the results were calculated until the COV = 0.05 showed the effect of greater scatter within the input parameters. For the variation of the Young’s modulus, the same coefficients are used to guarantee the comparability of the results.

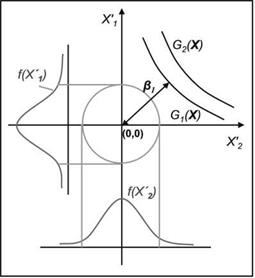
The allowed relative deviation A aEqSt / aEqSt of the converged angle of attack compared to the reference structure is analyzed in the range between 0.4% and 1.0% for different coefficients of variation. Each value of this deviation defines a limit state function G(X’). For a given value of G(X’) the FORM routine calculates a combination of random variables for which the reliability index converges. With regard to the investigated problem a combination of relative deviations of the struc­tural input parameters in each area was found for which the probability of a given deviation of the angle of attack becomes a maximum.

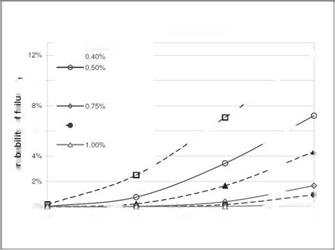
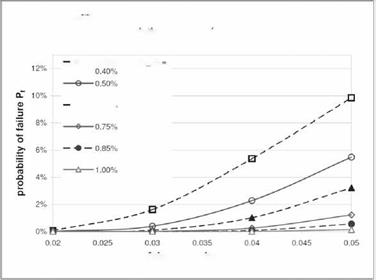
The results of the variation in the wall thickness and the Young’s modulus in skin areas are presented in figures 9 and 10. In the diagrams a probability of failure is plotted for a series of limit state functions over the coefficient of variance V. Due to almost linear correlation between the reliability index and limit state functions for a given COV, some curves could be extrapolated from the calculated results. These curves are plotted by dashed lines. For each limit state function the probability of the failure arises with the scatter in the input parameter expressed by V. The lower

Table 6 Areas of parameter variation

the allowed difference of the angle of attack expressed by a failure function is the higher is the probability to violate the requirements.

In the diagrams a probability of failure is plotted for a series of limit state func­tions over the coefficient of variance У. Due to almost linear correlation between the reliability index and limit state functions for a given У, some curves could be extrapolated from the calculated results. These curves are plotted by dashed lines in fig. 5 and 6. For the investigated coefficients of variance the results for a relative deviation of an angle of attack of 1.5% were calculated for the local variation in the skin thickness of 10% and more. This degree of variation within the wing structure seems not very realistic to be considered further. For each limit state function the probability of the failure arises with the scatter in the input parameter expressed by V. The lower the allowed difference in the angle of attack, expressed by a failure function the higher is the probability to violate the requirements.

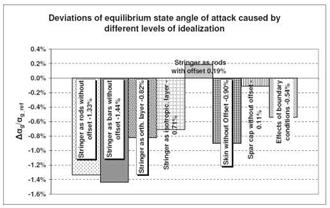
The comparison of the results for variation of skin thicknesses and Young’s mod­ulus shows very similar probability curves for both input parameters. The probabil­ity of failure obtained for the variation of Young’s modulus is somewhat smaller as for a variation of skin thicknesses. This tendency shows a good agreement with the predictions made within the sensibility study carried out in section 3.4.

From the results of the stochastic analysis depicted in figures 9 and 10 it can be seen that the probability of higher deviations (<1%) of the global aerodynamic properties of the wing still are very small even for a higher variance of structural parameters. This demonstrates a high robustness of the coupled fluid structure sys­tem affected by the considered type of uncertainty.

Є — AaEqSt/aEqStref

-* — 0.60”/

coefficient of variance V

Fig. 10 Probability of deviation of angle of attack caused by variation of Youngt’s modulus for different performance criteria

3.6 Conclusions In the present work, the influence of random structural parameters on the aerody­namic performance of a metallic test wing structure is investigated. The investiga­tions demonstrate the suitability of the FORM analysis to handle some classes of stochastic uncertainties affecting the aeroelastic response of a wing structure. Due to the gradient based optimization procedure, which forms the basis of the FORM the main requirement to the investigated problem is the existence of only one min­imum solution for the reliability index в. To handle problems which violate this requirement as there are the uncertainties of fibre orientation angles of composite materials, other stochastic analysis methods like Latin hypercube sampling should be used instead of the FORM. To reduce the numeric costs of stochastic simulation some simplifications had to be made within the analysis process. The influence of the weight reduction on the target lift caused by reduction of the wall thicknesses was neglected. The simultan­eous variation of structural parameters of the top and bottom skin in only four areas represents a highly simplified test case compared to the real structure (cp. the re­marks in section 3.4). Considering these simplifications, the results obtained in the present work should represent a conservative trend. The variation of the input parameters of top and bottom skin parts as well as of spar webs for a higher number of independent areas of variation is a part of actual work as well as the consideration of weight reduction for the target lift. Another effect which could be considered is the tendency of the skin areas to buckle if the

local bending stiffness of the panes is reduced by a variation of structural parameters having a significant influence on the aerodynamic drag.

References

[1] Heinze, W.: Ein Beitrag zur quantitativen Analyse der technischen und wirtschaftlichen Auslegungsgrenzen verschiedener Flugzeugkonzepte fur den Transport groBer Lasten; ZLR-Forschungsbericht 94-01, Braunschweig (1994)

[2] Osterheld, C. M.: Physikalisch begrundete Analyseverfahren im integrierten mul – tidisziplinaren Flugzeugvorentwurf; ZLR-Forschungsbericht 2003-06, Braunschweig (2003)

[3] Reimer, L., Braun, C., Bae-Hong, C., Ballmann, J.: Computational Aeroelastic Design and Analysis of the HIRENASD Wind Tunnel Wing Model and Tests. In: International Forum on Aeroelasticity and Structural Dynamics (IFASD) 2007, Stockholm, Sweden, Paper IF-077 (2007)

[4] Heinrich, R., Dargel, G.: Spezifikation des Testfalls fur den Hauptmeilenstein M8.1 im Verbundvorhaben MEGADESIGN (2006)

[5] Haupt, M., Niesner, R., Unger, R., Horst, P.: Coupling Techniques for Thermal and Mechanical Fluid-Structure-Interactions in Aeronautics. PAMM u Proc. Appl. Math. Mech. 5, 19-22 (2005)

[6] Schneider, W.: Die Entwicklung und Bewertung von Gewichtsabschatzungsformeln fur den Flugzeugvorentwurf unter Zuhilfenahme von Methoden der mathematischen Stat­istic und Wahrscheinlichkeitsrechnung; Berlin, Techn. Univ., Diss. (1973)

[7] Niu, M. C.Y.: Airframe Structural Design: practical Design Information and Data on Aircraft Structures. Conmilit Pr., Hong Kong (1999)

[8] Patnaik, S., Gendy, A., Berke, L., Hopkins, D.: Modified Fully Utilized Design (MFUD) Method for Stress and Displacement Constraints. NASA Technical Memorandum 4743 (1997)

[9] Malcolm, D. J., Laird, D. L.: Extraction of Equivalent Beam Properties from Blade Mod­els. Wind Energy 10, 135-157 (2007)

[10] Reim, A., Horst, P.: Structural optimization considering stochastic variations of manu­facturing alternatives. In: 8th World Congress on Structural and Multidisciplinary Op­timization (2009)

[11] Haldar, A., Mahadevan, S.: Probability, Reliability and Statistical Methods in Engineer­ing Design. Wiley & Sons (2000)

[12] Rackwitz, R., Fiessler, B.: Structural Reliability Under Combined load sequences. Com­puters & Structures 9, 489-494

The variation of the wall thickness and Young’s modulus causes a deviation of stiff­ness qualities of the wing structure. Due to manipulation of structural properties the tendency of the wing is affected to exceed its shape under a certain load. The object­ive of the parameter study was to estimate the impact of parameter variation within the main structural components on the structural behavior as well as on the static aeroelastic response.

The alteration of structural parameters of skin, spars, or ribs influences the tor­sion and bending distortions in different ways. Reduction of the wall thickness as well as of the Young’s modulus in the skin parts has the highest effect on the bend­ing and shear stiffness of the wing reducing the bending moment of inertia and shear coefficient of a local wing box cross-section. The torsional stiffness is also affected, depending on the ratio of wing box height to depth and thickness ratio of the skin to spar webs. Reduction of structural parameters in the spar webs influences mainly the torsional and shear stiffness having only a secondary effect on the bending mo­ment of inertia. Due to the low contribution of the ribs to the bending and torsional

stiffness of the wing box structure the variation of the input parameters in this struc­tural member has only a marginal effect on the deformation behavior of the wing.

A parameter study is carried out to estimate the sensitivity of the structural and thus of the static aeroelastic response relative to the components of the wing struc­ture affected by uncertain input parameters. The influence of each component is estimated by changing successively the wall thickness and Young’s modulus of the skin, spar webs and ribs. To avoid local effects both input parameters are varied sim­ultaneously by ±10% along the wing span. A structural and an aeroelastic response of a modified structure are determined for a reference loading corresponding to the 1g load case. From the structural response, the global deviations [Л0], [Aw’} and [Aael] of torsion deformation, bending angle and elastic angle of attack including the components [AOtr] and [Aw’tr] are calculated. An alteration AaEqSt / aEqSt of the converged angle of attack is obtained from the results of coupled analysis by com­parison with the reference structure. The results for the global deviations are given in tables 4 and 5.

The wing box investigated in the parameter study which structural properties are varied separately and in the same manner does not represent a real wing. An actual wing structure is assembled of many different parts of which the dimensions and material properties vary independently from each other. The intent of this simple

approach is only to estimate the main trend of the deviation of the output paramet­ers depending on the component of the structure in which the variation of input parameter occurs.

To estimate the tendency of change of the equilibrium state angle of attack aEqSt caused by the input variation of structural components a static aeroelastic response is calculated for each modified structural model already described. The relative de­viation of this angle is plotted in fig. 8 for each model derivate. The results show a good agreement with the tendencies obtained from the simple deformation study (see tables 4 and 5). The contribution of deviation of both deformation components to A aEqSt / aEqSt is somehow different for the variation of structural parameters in spar webs and rib surfaces. The change of the torsion angle is negative with respect to the sign convention showing therefore a stiffer torsional behavior. This tendency is due to the skewed root rib of a swept wing which influences the warping moment of inertia and, thus, the torsional behavior of the wing box.

A variation of the structural parameters shows the highest effect on the struc­ture’s stiffness and therewith on the change of the angle of attack in the skin areas as expected. The results of the structural response show that, in spite of a rather high ratio of the torsion angle to the elastic angle of attack, the latter is still domin­ated by the angle of bending deformation. The almost identical values obtained for A aEqSt /aEqSt by variation of both parameters of the skin parts should be treated as a special case taking into account the global character of the applied variations.

Fig. 8 Random input parameter distribution and limit state functions in the normal variable space

To apply the FORM analysis to the coupled fluid-structure problem a realistic failure criterion had to be defined to describe the performance of the simulated wing struc­ture. For this kind of problem the random input is given by a variation of structural parameters. The change of the converged angle of attack aEqSt of the aeroelastic equilibrium state (cp. section 1.2) was used to estimate the impact of random input parameters on the aerodynamic properties of the investigated wing model. The devi­ation A aEqSt/aEqSt can be considered in both positive and negative directions. The higher values of aEqSt caused by a lower Young’s modulus or by reduction in wall thickness, respectively, are assessed to be more critical than smaller ones, caused by a stiffer wing structure.

The probability of deviation of equilibrium state angle of attack is investigated for different values of AaEqSt/aEqSt varying between 0.4% and 1.0%. Each value corresponds to a limit state function in the normal variable space, which is defined as:

G(X’) = A aEqSt – AaEqSt, req (4)

The term AaEqSt req defines the highest permitted deviation of the converged angle of attack. For a discrete limit state function and a distribution of random para­meters (characterized by the coefficient of variance) the FORM algorithm calculates a combination of these parameters for which the reliability index в becomes min­imum. For the inversion of the argument, the probability of the aeroelastic response represented by the limit state function becomes maximal.

An exemplary problem for two random variables X[ and X[ with two limit state functions Gi(X’)) and G2(X) is depicted in fig. 7. Corresponding to the definition of the reliability index в the probability of G1 (X’) is higher then of G2(X’) because of the smaller distance в between the curve and the origin of the standard normal space.

To simulate an impact of variation of structural parameters on the aeroelastic re­sponse of the wing, the ifls-code-library was embedded into the routines performing the FORM algorithm. A NASTRAN input file of the finite element wing model was created with the ability to vary the structural properties during the stochastic pro­cess. Two input parameters are defined to be altered within the wing box structure: the thickness t of the thin-walled structural members and the Young’s modulus E of the material. For stochastic input parameters a normal distribution is assumed. The shape of the normal distribution and, therefore, the extent of the deviation of the input parameters are characterized by the coefficient of variation (COV) V = ст/д. The COV is defined as a ratio of the standard deviation ст to the mean value д. For a random variable with V = 0.1 the probability is 31.7% that the deviation of this variable exceeds ±10%.

In the present work, the probability of failure Pf of the wing structure is computed. It describes the probability that the structure does not to comply with the predefined requirements. Thus, the term failure has to be distinguished from other terms, like e. g. crash or disaster. Since the coupled fluid-structure analyses are very time con­suming, the first order reliability method (FORM) was implemented to calculate the stochastic characteristics of the wing [10]. FORM introduces the reliability index в to describe the reliability of the structure. The main input to the method is the limit state function G(X), where X is the vector of stochastic variables that influence the structure. By definition, the limit state function is positive, if the structure fulfils its requirements. Negative values are returned, if at least one requirement is violated.

In order to generate unique results for every problem, the vector of stochastic variables is transformed into a vector of standard normal random variables X. This leads to a limit state function G(X’) which is analyzed using the FORM routine. The FORM is a gradient based optimization procedure which calculates the minimum distance в between the limit state function defined by G(X’) = 0 and the origin of the standard normal variable space spanned by the normalized stochastic variables.

At the beginning of the FORM algorithm, a віпШаї has to be estimated. The bet­ter the estimation of this initial value factor the fewer iterations are needed in the algorithm to get the final в. With the вмш and the limit state function value, all parameters are defined to start the main iteration of the FORM algorithm consisting of three main steps: (cp. Haldar, Mahadevan [11])

• Transformation of stochastic variables into standard normal variable space. In order to get unique results, all non-standard normal variables have to be trans­formed. For normal variables, a general conversion can be applied, for other variables, the Method of Rackwitz and Fiessler [12] has to be used.

• Generation of derivatives of the limit state function with respect to the standard normal variables. The coupled fluid-structure model can not be solved algeb­raically. Thus, the derivatives have to be estimated by finite differences in the neighbourhood of the design point.

• Calculation of the direction, where the steepest trend in the limit state function occurs and estimation of a new design point and the corresponding в value

This iteration is repeated until the limit state function value is zero and the в value converges. The resulting в value is then transferred to the fitness value calculation routine of the optimization.

1.3 Introduction

In the second part, the effects of stochastic uncertainties on the accuracy of static aeroelastic analysis are investigated. A parametric finite element model (see section 1.1) is used to simulate the scatter of the structural input parameters expressed as Gaussian standard normal distribution. Coupled aeroelastic analysis is performed to obtain the deviation of the wing aerodynamics for a discrete distribution of the stochastic input parameters using a high order panel code. A first order reliab­ility method is employed to calculate the probability of change of aerodynamic performance parameters due to the variation of structural stiffness properties. The results of the stochastic analyses performed for a simple test case are presented and demonstrate robust behavior of a coupled aeroelastic system subjected by moder­ately arbitrary structural parameters.

Effects occurs by modeling the spar caps with beam or rod elements with or without considering element offsets are similar to those discussed in the section above. Due to smaller cross-section of the spar caps relative to the cross-section of the whole wing box this effects causes only marginal discrepancies of the bending and tor­sion angle and thus of the elastic angle of attack. If spar stiffeners are considered as isotropic layer in the wall thickness of the skin parts the bending stiffness in­creases causing 0.8% smaller elastic angle of attack. The deviation [Aael] that res­ults from neglecting the element offsets varies between -0.46% and -0.54% (see fig. 4). A static aeroelastic response was calculated for wing structure with spar caps modeled with bar elements without element offset. The converged angle of attack

aEqSt of this structure is only 0.11% smaller compared to the reference structure. How can be seen from results in table 4 the influence of rib caps on the bending and torsional deformation is marginal resulting in deviations of elastic angle of attack being between 0.02% and 0.2%. Therefore, the influence of these stiffening com­ponents on the deformation behavior and thus on the aerodynamics of the wing can be neglected.

1.2.1 Conclusions

Within the first part of the work, a simple method was presented to calculate global parameters, which enables to estimate the effect of uncertainties of structural mod­els on the deformation behavior and thus on the aerodynamic properties of the wing structure. This method was applied to investigate the impact of modeling uncertainty on the structural and aeroelastic response of the wing of a wide-body transport air­craft. The results of the study yield a rather good agreement between the deviation trends of the structure subjected to modeling uncertainty, which are calculated for a static loading and the discrepancy of aerodynamic properties of the wing obtained by a coupled analysis. As mentioned above, the elastic angle of attack ael, employed as evaluation parameter is dominated by the bending deformation of the wing struc­ture. Since the top and bottom covers have the greatest contribution to the bending stiffness of the wing, the simplified modeling of stringers has the major effect on the accuracy of the structural model. The deviations of converged angle of attack aEqSt, used as performance criterion to evaluate the accuracy of the coupled analysis varies between 0.2% and 1.44% for different degrees of modeling detail (see fig. 6).

As shown on the sample of simplified boundary conditions, the higher deviations of twist and bending angle must not as well produce higher discrepancy of con­verged angle of attack. In fact the deviations has to be transformed in flight direction using the interrelationship give in equation (2) to estimate the resulting effect of the discrepancies within both deformations on the load distribution.

In the following sections, the effects of the different degrees of detail of modeling are discussed. Several types of stiffener idealization are considered and the effect of the simplifications on the structural behavior and aerodynamic properties of the wing is evaluated by calculating structural and static aeroelastic response. The devi­ations of structural response computed for each case are summarized in a test matrix (see fig. 4). In the test matrix, different degrees of modeling detail are considered for stringers, spar caps and rib caps. The levels of modeling detail are represented by realizing the structural member by beam elements or rod elements, or by homo­genizing the stiffeners as isotropic or orthotropic layer. The effect of element offset is also considered for beam and rod elements as well as for the orthotropic material layer. For the main idealizations, the deviation of converged angle of attack from the reference case is plotted in figure 6.

Effects of Simplified Stringer Modeling

Explicit modeling of stringer stiffened top and bottom covers including property as­sociation for stiffening members is very time-consuming especially if the stringer cross-section geometry varies in both chord and span wise directions. Several de­grees of stringer idealization are considered within the present study. A common method to avoid the modeling effort is to create a skin-stringer-"laminate" with iso­tropic skin and orthotropic stringer layers. The benefit of this approach is that only one parameter is required to realize the skin-stringer-structure. This parameter is the area ratio of the skin and summarized stringer cross-sections, commonly given in the literature as 100:50 for thee design of transport aircraft wing structures [7]. The structural model with stringers smeared as an isotropic layer presents the simplest approach concerned in the present study.

Homogenizing discrete stringers over the skin area has two opposite effects on the bending stiffness of the wing box. The first effect is the reduction of the wing box local moment of inertia by neglecting the bending stiffness of the stringers. The second effect is the overestimation of the wing bending stiffness caused by neglect­ing the (offset) distance of the stringer cross-sections relative to the skin surface. The effect of ignoring the bending stiffness of the stiffeners on the bending and tor­sional deformation of the wing can be concerned on the basis of deviations obtained for a FE model with stringers realized with rod elements. For this idealization, the bending angle is increased by only 0.84% due to lower structural stiffness, resulting in 0.87% greater angle of attack. The influence of stringer stiffness on the torsional behavior and in turn on the elastic angle of attack is negligible (see table 4). The marginal impact of stringer bending stiffness on the deformation behavior results in change of geometric angle of attack being only 0.19% (see fig. 6).

In contrast to the effect of the stringer-stiffness, the overestimated contribution of the stringer-cross-sections to the local wing box moments of inertia due to non­considering the correct offset distance dominates the influence on the bending de­formation. How can be seen in table 4 for the deviations obtained for FE models with stringers idealized as isotropic and orthotropic layer without offset, the bending angle decreases by 3.9 — 4%. Because stringers do not contribute to the shear load resistance of skin panels the stringer idealization as an orthotropic material layer enables to reproduce the torsional stiffness of the wing box structure in the way that

is more realistic compared with stringers homogenized as isotropic material. This trend is demonstrated by the smaller deviation of twist ( [AQ] = 1.1%) compared to the simplest model ([A0] = 6.3%). One remarkable effect of greater difference of wing twist is the smaller deviation of elastic angle of attack of the structural model with stringers idealized as isotropic layer ([Aael] = -3.4%) compared with the more realistic approach ([Aael] = -4.1%). The trend predicted by the comparison of the [Aael]-deviation parameters between the both structural models, confirms with the results of static aeroelastic analysis. The deviation of converged angle of attack for the skin-stringer compound realized with orthotropic stringer layer is slightly higher (AaEqSt / aEqSt = -0.82%) as for a simpler structure (AaEqst/aEqSt = -0.71%, see fig. 6).

To reproduce the outer mold surface of the real wing structure the shell elements forming the wing skin must have an offset relative to the nodes of the discretized geometry. By neglecting the element offset the distance of skin panels relative to the neutral axis of the wing box will be overestimated. This effect will increase the moment of inertia of the wing box cross-section following the parallel axis theorem, which in turn results in higher bending stiffness of the wing structure compared to the exact solution. The torsional stiffness will also be affected by the in­creasing distance between the mid-lines of the top and bottom covers in accordance with the Bredt-Batho formulation. The same effect on the bending stiffness appears by ignoring the offset distance of beam or rod elements representing the stiffening structural members. The latter case will be considered separately for each stiffening component.

To estimate the impact of the modeling simplifications on the deformation beha­vior of the wing box the structural response is calculated for the idealized and the reference structural models. The integral values of the deviation in bending angle, torsion and resulting elastic angle of attack compared to the reference structure are given in table 3. For the FE wing model without element offset within the top and bottom covers the bending stiffness increases accordingly to the a. m. effects result­ing in an approximately 4% smaller bending angle which in turn reduces the local angle of attack (cp. section 1.2). Torsion deformation is also reduced by 1.7% due to the higher torsional stiffness having an opposite effect. The change in both degrees of freedom results in 4.1% smaller elastic angle of attack due to the dominant in­fluence of the bending stiffness (compare the values [Aw’]tr and [AQ]tr in table 3). The sign of the transformed deviation parameter [AQ]tr changes due to the relation to the maximum value of elastic angle of attack a^.

The converged angle of attack calculated for the more simplified structure shows a 0.9% smaller value compared to the reference model (see fig. 5). This result cor­responds with the trend predicted by the negative change of the elastic angle of attack [Aael} given in table 3. Smaller (negative) values of ael (y) along the span have a reduced effect on the load distribution compared to the reference structure and, therefore, the target lift can be achieved under smaller angle of attack.

Table 3 Deviations of bending angle, torsional angle and elastic angle of attack for different states of modeling simplification

At the root, the wing is mounted to the wing center box and to the main frames of the fuselage. Despite of high local wing box stiffness, a minimal translational displacement of the wing skin in span wise direction is possible in the root area. If this infinitesimal displacement is constrained by restriction of all translational and rotational degrees of freedom along a root rib curve (see fig. 3, on the right hand side), a reduction of bending and torsion deformations due to the overestimation of wing root rigidity can appear. This kind of idealization is used when the structure of a half wing is realized without the center box. To assure realistic boundary condi­tions, see figure 3 on the left hand side, the displacement of upper and lower edges of the root rib, should be constrained only in direction normal to the skin surface (z-direction). The nodal displacements in spanwise direction (along the y-axis) as well as nodal rotations have to be constrained only at the symmetry plane of wing center box.

The effect of higher wing root rigidity has a local character influencing the bend­ing and torsional deformations in the form of additional (negative) rigid body mo­tions, resulting in the integral deviation of 5.4% within the bending and approx.

30% within the torsional angle. Due to the mutually directed influencing tendencies of these deformations, the resulting change within the elastic angle of attack is only 1.8% (see table 3). From the transformed values and [AQ}tr in table 3 it can

be seen that the rather high contribution of bending deviation in flight direction is compensated by the much higher change of the torsional angle.

The results of the coupled aeroelastic analysis confirms with the tendency of the deviation of elastic angle of attack ael (y) obtained by the structural response. This moderate tendency of the change of is reflected in the deviation of the equilibrium state angle of attack AaEqSt /aEqSt being only 0.54% (see fig. 5).

A series of comparing analyses is carried out to estimate the influence of geometrical details on the accuracy of wing structural response. Global deviation parameters presented in section 1.2 are used to evaluate at first the change in structural stiffness components due to modeling approximations and secondly the influence of these alterations on the static deformation of the wing in flight direction considering the elastic angle of attack ael. For selected cases a static aeroelastic analysis is carried out to calculate the deviation of equilibrium state angle of attack and, therefore, to estimate the impact of altered structural stiffness on the aeroelastic response. To

stiffeners: rod elements

spars

stiffeners smeared

skin-stringer-

panels

Fig. 2 Components of the wing box structure

distinguish the deviations of structural stiffness five integral parameters are listed in tables 3 and 4 for each modeling effect. These parameters are the integral deviation of bending and torsional angles [Aw’} and [AQ] relative to the elastic axis of the wing, the "transformed" values [Aw’}tr and [AQ]tr of both angles in flight direction as well as the global deviation of elastic angle of attack, [Aael}.