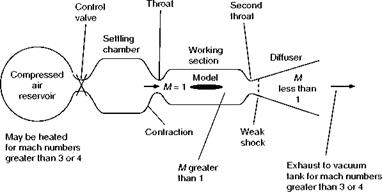
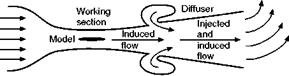
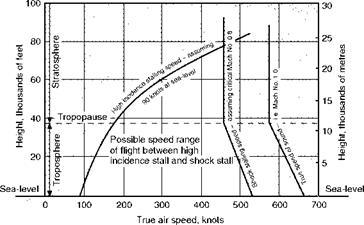
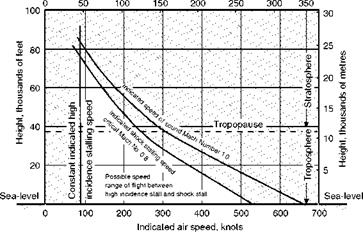
Control problems
Reference has already been made to the unpleasant things that may happen to aircraft as they go through the speed of sound – violent changes of trim, up or down, oscillations, buffeting, and so on. In such circumstances the first essential from the pilot’s point of view is that he should have complete control; and so be master of the aircraft and its movements.
Unfortunately this is by no means easy to provide – and for several reasons.
Consider, for instance, an ordinary tail plane and elevator. At subsonic speeds an elevator depends for its effectiveness on the complete change of flow which occurs over both tail plane and elevator when the elevator is raised or depressed; the actual forces which control the aircraft are in fact much greater on the tail plane than they are on the elevator itself. Now as soon as a shock wave is formed on the tail plane – and the most likely place for its formation is at the hinge between tail plane and elevator – a movement of the elevator cannot affect the flow in front of the shock wave, so we have to rely entirely on the forces on the elevator itself to effect control. But the elevator will be in the turbulent flow behind the shock wave, and so may itself be very ineffective in producing the control forces required.
At higher speeds, when the shock wave moves back over the elevator, the opposite trouble may occur, and the forces on the elevator may be so great that it becomes almost immovable.
The answer to these troubles has been found in the all-moving slab type of tail plane (Fig. 5H) – sometimes given the rather curious name of a flying tail – and in making this power-operated. In this way we have what at the same time is an adjustable tail plane and an elevator.
The same principle can be applied to the ailerons – by having all-moving wing tips – and, more rarely, to the rudder, by having a combined fin and rudder.
But this is not the only high-speed control problem. Another is the possibility of reversal of the controls, owing to the distortion of the structure by the great forces on the control surfaces. This is most likely to happen on the ailerons. Suppose, for instance, that the starboard aileron is lowered in order to raise the starboard wing – if the force on the aileron is very great it will tend to twist the wing in such a way as to reduce its angle of attack, and so reduce the lift instead of increasing the lift on that wing; and the net result is that the wing will fall instead of rise. The aileron is acting on the wing just as a control tab is intended to act on a control surface; but that is little consolation to the pilot, and it doesn’t take much imagination to realise his horror when a movement of the control column has exactly the opposite effect to that intended! Nor is it an easy problem for the designer to solve since the extra weight involved in providing sufficient stiffness, especially on thin and heavily swept – back wings, may be prohibitive. So as well as requiring power-generated controls, special high-speed ailerons may be needed – these are situated well inboard where the structure is stiffer instead of at the tips. Another solution is to use ‘spoilers’ instead of ailerons. These are small flaps which come out of the top surface of the wing and disrupt the local flow, thus reducing lift on that wing and giving rolling control.
The introduction of power-operated controls has in itself caused a new problem in that the pilot no longer ‘feels’ the pressure resisting the movement of the controls; this feel was always a safety factor in that it made the pilot conscious of the forces he was applying, and in fact there was some advantage in that there was a limit to what he could do to the aeroplane owing to the sheer limitation of his strength. So important is this matter of feel that when power-operated controls are used it has been necessary to incorporate artificial or synthetic ‘feel’; and this is made even more real by grading it so that it varies not only with the movement of the control surface but with the density of the air and the air speed, in other words with the dynamic or stagnation pressure, ypV2 or q – it is sometimes called ‘g-feel’. Quite apart from the safety aspect, this synthetic feel gives the pilot a sense of control over the aeroplane which restores something of the art of flying.
But this is not the only problem resulting from the use of powered controls. If the power fails, and if there is no means of reverting to manual operation, the control may lock solid and the pilot be denied the use of rudder, elevators or ailerons. The answer to this is to introduce a safety factor by having more than one control surface, each having a separate power control; thus the Concorde had two rudders, one above the other, and six elevons (combined elevators and ailerons, which is the usual arrangement on delta or highly- swept wings). The Russian counterpart even had eight elevons.
Again on delta and highly-swept wings there is sometimes an interesting use of spoilers, this time as an aid to longitudinal control. Targe aircraft flying at high speed, with their considerable inertia, are slow to respond to the elevators, just as they are to the ailerons. If one set of spoilers is fitted inboard (i. e. close to the fuselage) on each wing, and so forward of the aerodynamic centre; and another set is fitted well outboard and so, owing to the sweepback, behind the aerodynamic centre; and these are then linked to the elevator control in such a way that the fore and aft sets can be operated differentially, they will cause a movement of the centre of pressure which will aid the elevator control, just as when they are operated differentially on the port and starboard wings they assist the ailerons in providing lateral control, as described above.