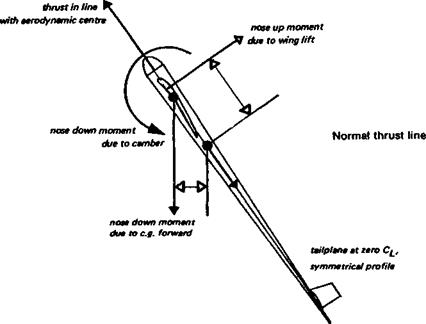
It is apparent from Figure 13.1 also that an aerobatic model with a symmetrical wing profile will hardly suffer from any adverse drag effects of aileron applications. The profile drag curve moves with the aileron, so, contrary to many statements in articles hitherto, there is no increase of profile drag caused by the downgoing aileron, and no decrease on the other side. There is, however, an increase in ci on one side and a decrease on the other. This does cause a variation of the vortex-induced drag, more lift on the rising wing creates an induced drag force tending to slow that wing down, while on the downgoing side, less lift creates less induced drag, tending to speed that wing up. A high speed model with a symmetrical profile will normally be operating at a low Cl in the first place, and induced
|
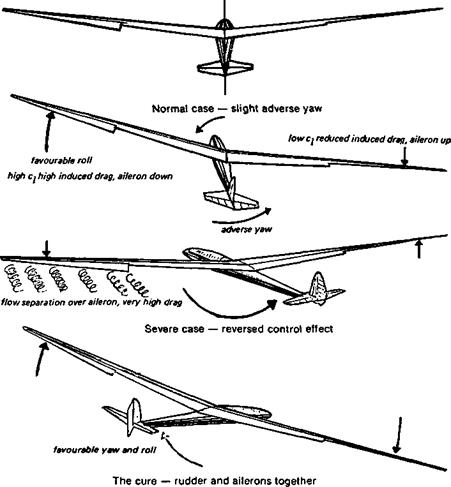
Fig. 13.3 Aileron drag
+ differential ailerons
|
drag, as shown in Fig. 4.9, is small at high speeds and low angles of attack. It is possible to ignore the ‘adverse yaw’ effect of ailerons alone. If a slight adverse yaw is noticeable, when flying slowly, it can be corrected by use of the rudder, but for normal aerobatic flying, and on racing models, ailerons are the essential turning controls and rudder is employed mainly to counteract yaw due to slipstream effects. Exactly the same applies with full-sized, fast light aeroplanes.
At low speeds and especially on sailplanes with large span, induced drag is dominant and the adverse drag caused by ailerons is serious. As the aileron on one side moves down the local ci, already high because the model is flying slowly, rises still more, and the induced drag increases sharply on that side, tending to yaw the model against the desired direction of turn. On the other side, the ci drops, induced drag falls, which aids the adverse
yaw (Fig. 13.3). If the model is operating close to the edge of the wing profile’s low drag ‘bucket’, it is quite likely that this increase of induced drag on the upward moving wing (down-aileron side) will be supplemented by an increase of profile drag, caused by flow separation over the aileron. This will be particularly likely if the ailerons are badly designed with a clumsy hinge line, or gaps promoting flow breakaway. In extreme cases the adverse yaw caused by the ailerons may be so severe that it overcomes the rolling •effect due to the lift imbalance. The model in such a case will yaw violently away from the turn, the slow moving wing with aileron down may actually develop less lift than the fast moving one with aileron up (lift force depends on airspeed), and the turn will be the opposite of that desired by the pilot Some very early types of full-sized sailplane suffered from this effect at low speeds, while at high speeds the torsional flexibility of their wings also rendered ailerons ineffective. Only within a narrow speed range between did the ailerons work. Some model sailplanes suffer from similar troubles. On a sailplane at low speed, it is essential to use the rudder with ailerons to initiate a turn. There is an excellent case for coupling of ailerons and rudder, the adverse yaw of the ailerons being countered by simultaneous application of rudder. Modem radio control equipment makes such coupling very easy and it may be switched in or out as required, in flight
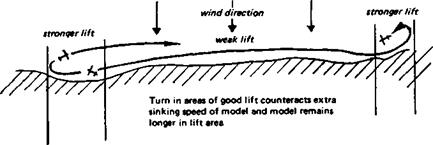
As a rule, some elevator action to control flying speed is necessary. In any turn, some of the wing lift force is directed horizontally, but the model’s weight must still be balanced by the vertical lift component (Fig. 7.8). This requires either an increase of speed or the wing must operate at a higher Cl, and hence a higher angle of attack, than in level flight Since a soaring sailplane is likely to be operating already close to the stalling angle, it is necessary to increase the flight speed in a turn to avoid a ‘wing drop’ caused by the inner wing in the turn stalling. This implies a steeper glide angle in the turn, and a higher sinking speed. The steeper the turn, the greater the loss of efficiency. In thermal soaring, since the model must turn to remain in the thermal, some penalty in performance has to be accepted. In hill soaring, the loss is small and in good or moderate conditions is hardly noticeable. However, in weak lift, the height lost on turns may be just enough to make soaring impossible. In such conditions it is common to find small patches of better ‘lift’ here and there along the slope, with weak or even nil lift between. If the turns are made in the better spots, not only is the increased sinking speed in the turn more likely to be overcome, but the model remains in the rising air longer than if it were allowed to fly straight through it The ‘beat’ worked on such a day, if possible, should thus begin and end in rising air, with straight flight between through weaker areas (Fig. 13.4). Note that all turns must be correctly banked. A flat, skidding turn creates excessive drag and increases sinking speed.
Once in the turn, a model with spiral stability will continue to turn with centralised controls until brought straight again by opposite aileron and rudder. This is a desirable
|
Fig. 13.4 Hill soaring in weak lift
|
state of affairs but may require various adjustments of dihedral angle, fin area, and gearing of rudder and ailerons, before being achieved. ‘Holding off excess bank with ailerons is usually necessary to some extent with large span aircraft
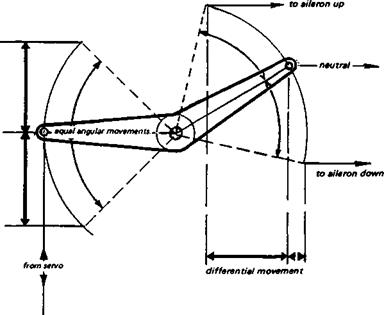
Some reduction of the adverse aileron yaw effect can be achieved by gearing the ailerons differentially. This is easily done by arranging bell cranks in the control circuit as shown in Figure 13.5 or by electronic means. The down-going movement will be less than the upward deflection, so the bulk of the rolling effect will come from the reduction of lift on the wing inside the turn. Differential ailerons cannot altogether overcome adverse yaw. The rudder is still essential for a clean turning action. Other devices, such as the Frise aileron (Fig. 13.9) or spoilers which open on one side as the aileron on that side goes up, are effective but cause increased drag and should be adopted only if all else fails.
The disadvantage of mechanical coupling of ailerons and rudder is that some special manoeuvres such as sideslips, in which the model is deliberately yawed away from the down-going wing to increase fuselage drag (so descending faster without increase of airspeed), cannot be performed. On rare occasions it may also be more difficult to enter and recover from spin, because the aileron deflection changes the stalling angle of the wing tips. In aerobatics, rolls are often accomplished by ailerons and rudder working independently.