Doppler Effect
In Curle’s formulation (section 4.6) we restricted ourselves to fixed control volumes. When considering sound produced by moving objects such as fan blades, it is more convenient to use a moving control volume. Ffowcs Williams and Hawkings (1969b) use generalized functions to take into account the motion of the sources, the result being a generalization of Curle’s equation in which Doppler factors appear. In a further step Ffowcs Williams and Hawking [Goldstein (1976), Dowling and Ffowcs Williams (1983), Crighton et al. (1992)] introduce the boundaries of the control volume in the equation of motion, see next chapter. We now focus on the derivation
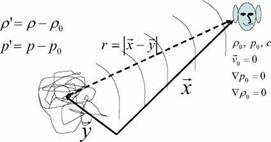
of the Doppler effect for point sources. A moving point source is described by:
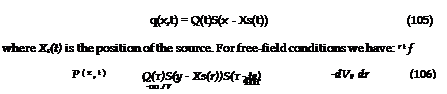
![]()
where te = t – r and r = x – y. Using the properties of the delta function we get after spatial integration:
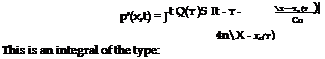 |
|
|
|
|
|
|
|
![]()
with H(ti) = 0. In the present case we have:
![]()
![]() x – xs (t)
x – xs (t)
Co
|
|
|
|
where Mr is the ratio of the source velocity component in the direction of the observer and the speed of sound. The sound field is given by:
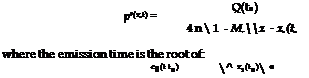 |
|
|
|
|
|
![]()
For subsonic velocities there is only one root (t = te) of H(t) = 0. For a harmonically oscillating sound source with constant frequency ш, the frequency of the signal reaching the observer is:
dwte ш
dt 1 – Mr (te)
because d = (tc).
A further discussion of the Doppler Effect is provided in the next chapter, where it is shown that for supersonic Mach numbers, the sound source will have a strong radiation for directions such that Mr = 1. An example of such a radiation occurs when elastic bending waves in a plate propagate supersonically with respect to the surrounding fluid. As the velocity of propagation of bending waves increases with the frequency this occurs typically above a critical frequency fc, which is called the coincidence frequency. This explains why we hear a high pitch when we hit a glass window.
From equation (111) we observe that in addition to the change in frequency we have an effect of the source motion on the amplitude reaching the observer. This effect can be understood as a result of the change in ratio of source size to acoustic wave length. From equation (63) we know that with increasing Helmholtz numbers the radiate sound amplitude of a compact object increases. In the direction of motion of the source, the emitted acoustic wave length is shorter by a factor 1 — Mr, with an increased effective Helmholtz number as a result. In figure 5 we provide an intuitive interpretation of the Doppler shift in frequency.
Furthermore we note that for a moving object of volume V the sound source is q(x, t) = p0dVS(x — xs(t)). Hence we have:
It shows that due to the time dependency of the retarded time dte/dt an object of constant volume will radiate sound if its velocity varies. This is the so called thickness noise p’th, which is very important in aircraft fans. In the far field approximation for a rigid of volume V body moving at subsonic speed, we have:
Another example is the sound radiated by a moving point force:
f = F (t)S(x — xs(t)) (116)
which is given by:
|
In the far-field approximation we have:
![]() F(te) .
F(te) .
4п|x – xs (te )||1 – Mr (te) | ‘
(118)
4.8 Influence of speed of sound gradient and of convective effects
Whenever a source of sound is compact we can separate the sound generation from the wave propagation. Even with this simplification the wave propagation remains extremely complex.
In the presence of flow and gradients in the speed of sound, acoustic
waves display complex propagation behaviour [Dowling 1983, Pierce 1990, Rienstra 1999]. An example of this is the sound propagation in the atmosphere. As a result of the non-uniformity of the temperature in the atmosphere waves are deflected from the straight path assumed in the elementary solutions for uniform stagnant fluid. An example being that a gun shot or thunder heard at large distances can be repeated multiple times, which yields a roll sound. This is due to the fact that sound can reach our ears along multiple paths.
We now consider a very basic problem of a plane wave that is reflected at the interface (shear layer) between two uniform media a and b with each having uniform flow speeds respectively Ua = (Ua, 0, 0) and Ub = (Ub, 0, 0) and speeds of sound ca and cb respectively.
In presence of a uniform flow the plane wave solution (52) becomes:
![]()
![]() Ux Un
Ux Un
co + n ■U,
with П = (cos в, sin в, 0) and к = un/(c0 + П ■ U).
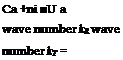 We assume an incident wave with amplitude I and wave number ki = in region a. This induces a reflected wave with amplitude R and
We assume an incident wave with amplitude I and wave number ki = in region a. This induces a reflected wave with amplitude R and
 and a transmitted wave with amplitude T and (Figure 6).
and a transmitted wave with amplitude T and (Figure 6).
Cb+UT■Ub V & ’
At the interface x2 = 0 we have continuity of pressure so that for x2 =0 we have:
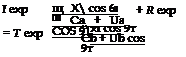 |
|
|
|
![]()
As this equation should hold for any value of the coordinate xi (along the shear layer) the exponents should be identical:
![]()
cos вІ
Ca + Ua cos ві
cos eR
Ca + Ua cos вП
cos вт
cb + Ub cos вт
The first equality of (121) implies that cos в1 = cos eR, so that the reflection angle is equal to the incidence angle eR = —вІ.
The second equality of (121) yields the modified Snelius law:
ca
cos вІ
cb
cos вт
Ub = (Ub,0,0)
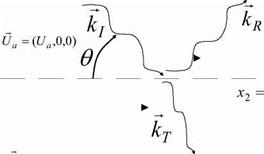 |
Figure 6. Reflection and refraction of a plane wave at a flat shear layer x2 =0 separating two uniform flows.
or:
The maximum transmission angle is found for grazing incidence cos вІ = 1: In the particular case of ca = cb and Ub = 0 we find:
In high speed jets one does indeed observe a cone of silence along the axis of the jet, because the acoustic waves emitted along the main flow direction are bent away from the flow direction by the velocity gradient in the shear layers [Morfey (1978)].
The amplitude of the transmitted and reflected waves is calculated from the continuity of pressure at the interface I + R = T complemented by the continuity of particle displacement at the interface.











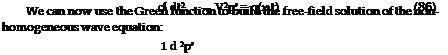
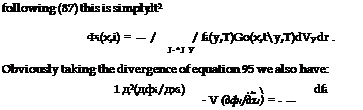
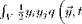 dVy і…
dVy і…