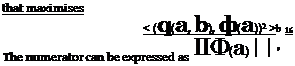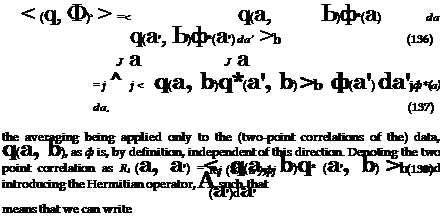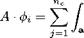Basic Assumptions – Thin-Airfoil Linearized Theory
For the mathematical statement dedicated to analytical investigations, is defined as unsteady aerodynamics any lift variation on an airfoil due to a variation in the oncoming flow (speed or angle of incidence), for which the Kutta condition of no flow around the trailing edge has to be fulfilled. Such a mechanism involves the entire airfoil section. The theoretical determina-
![]()
tion of £(t) would be certainly a considerable task, were the exact solution sought for each practical flow field of interest, because of the variety encountered in both airfoil shapes and surrounding flow conditions. But acoustic calculations benefit from the favorable effect of the logarithmic dB-scale, and often only require a consistent approximation of £(t) in most cases of interest (rotating blades, high-lift devices). For subsonic thin airfoils with small camber and angle of incidence, referred to as slightly loaded airfoils, and small velocity fluctuations, the linearized unsteady aerodynamic theory described below provides helpful approximate solutions. In contrast for highly cambered, thick blades, such as the ones encountered in turbine blade rows, the linearized approach is not relevant, and a numerical analysis is required.
![]()
![]()
![]()
 Лпе
Лпе
«•sS»***
SUCTION SIDE TE
Figure 2. General airfoil definition. a and Z are the angle of attack and the maximum camber displacement, respectively.
Before listing the assumptions of the linearized thin-airfoil theory, let us perform first a rapid analysis in the two-dimensional framework of Fig. 2. U0 is the mean flow velocity, at an angle of attack a with respect to the chord line. Consider the velocity fluctuation vector u = (u, w) superimposed on the mean flow and defined in absence of airfoil. u is the variation of velocity magnitude along the average flow direction and w the variation of angle of attack.
A first insight into unsteady aerodynamics is provided by perturbing the steady-state equation relating the lift force per unit span F0 to the relative velocity U0:
where CL is the lift coefficient, function of the angle of attack a, and c the chord length (Fig. 2). Small variations of the angle of attack and of the magnitude of the velocity vector then lead to the differential
This is a quasi-steady approximation because eq.(1) is assumed to hold also for transient flow conditions. For weakly loaded airfoils it can be assumed that CL ^ 1 ; furthermore dCL/da = 2 n for a Joukowski airfoil. It is concluded that whenever the incident velocity disturbances w and u have the same order of magnitude, the component w is responsible for the major part of the unsteady loads. The assumptions are better justified for moderately cambered airfoils or lifting surfaces. Intuitively, blowing on a flat plate parallel to its surface and varying the flow speed is not expected to induce lift variations, whereas slightly changing the angle of attack produces significant ones. In contrast, variations of the flow speed Uo at constant angle of attack on a highly cambered surface are known to also generate large lift fluctuations, as suggested by the vertical efforts exerted on an umbrella in a varying wind. As a consequence, only the fluctuations of angle of attack are generally considered in linearized unsteady aerodynamic theories applied to slightly cambered airfoils. Highly cambered airfoils are not considered here; they would require numerical investigation.
Obviously the direct proportionality and the immediate response of the airfoil expressed in eq.(1) are abusive. Indeed by virtue of the Kutta condition, vorticity is continuously shed in the wake as a result of any inflow variation. The evacuation of the shed vorticity in the flow requires a finite time, which results in some delay of the force variation. The quasi-steady approximation is just the asymptotic form of a needed more general description; it is valid for very slow variations or for large flow patterns with respect to the dimensions of a body in a flow (see Fig. 1-a again). Part of the broadband noise from low-speed fans is predicted based on similar arguments by Sharland (1964) and Fukano et al (1977).
Anyway, as shown by the pioneering work by von Karman & Sears (1938), cited by Goldstein (1976), small thickness, camber and angle of incidence only determine the steady lift, but have no significant effect on the unsteady loads. This fundamental decoupling of the unsteady aerodynamic behavior from the mean loading has very important implications. Typically it means that lift fluctuations can be determined independently of the airfoil design by just solving the problem of the response of a thin flat
plate embedded at zero incidence in a parallel mean flow carrying normal velocity disturbances. This will be called Sears’ problem in this course.
The general approach for solving Sears’ problem in two or three dimensions is described now. First of all, the incident disturbances are assumed frozen, which means that their decaying time is large in comparison with a characteristic traveling time along the chord length. They are rotational in essence but the additional disturbance induced by the airfoil can be described as a potential field, apart from the wake; the part of this field which propagates away from the airfoil is precisely the acoustic motion. Secondly the solution is derived in the frequency domain because the time delay produced by the Kutta condition must be compared to the characteristic period of the variations of angle of attack. The procedure is as follows.
1 – The oncoming velocity disturbance normal to the airfoil surface (up – wash) is Fourier-analyzed. Each Fourier component defines a transverse sinusoidal gust in the sense of unsteady aerodynamics. A gust is characterized by the chord-wise aerodynamic wave number k1 and, because of the convection speed U0 , induces forces on the airfoil at the corresponding angular frequency ш = k1 U0 . A spanwise aerodynamic wavenumber k2 is also introduced when the theory is extended in three dimensions (Fig.5 ).
2 – At a given value of ш or ki, the Fourier coefficient E(ki) of the total unsteady lift force is determined by some unsteady aerodynamic theory in terms of the transverse fluctuation amplitude rw(k1) . In order to connect the formal result eq.(1), it is written:
E(ki) = n po Uq w cT,
where T is some aerodynamic transfer function introduced for physical consistency to account for the phase shift between the lift variations and the variations of angle of attack. More precisely the local distribution of fluctuating lift along the chord line, say £(k1,y1) where y1 is the chord-wise coordinate, may be of interest. For acoustic purposes, the integrated lift is enough if the chord length is acoustically compact, but the distributed local lift is needed if it is not.
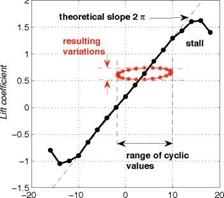
The phase shift results in an inclined hysteresis response curve in the plane (a, Cl) (Fig. 3). Instead of following the steady-state curve, the operating point of the airfoil follows that hysteresis loop, centered around the mean-value point. The amplitude of the lift variations is well smaller than what the quasi-steady approximation would predict. The figure also suggests that oncoming disturbances can prevent the airfoil from stall. Indeed wind-tunnel experiments and simulations on oscillating airfoils have confirmed this point.
 |
Angle of attack (°)
Figure 3. Typical aerodynamic lift coefficient curve of an airfoil (steady state) and illustration of the unsteady aerodynamic response to cyclic variations of the angle of attack.
3 – The contribution of the gust to the far-field sound is derived, based on the acoustic analogy.
In this procedure the key step is the relationship between the incident velocity disturbances, assumed known, and the associated lift variations, still to be determined. A minimum review of available theories achieving this step is given below. It must be kept in mind that in practice information about velocity disturbances is generally of easier access than information about the wall pressure on a body.












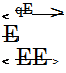
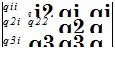 Qi
Qi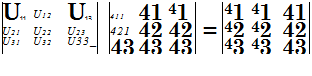
 (165)
(165)